Kinematics

Position

In mechanics the position of a body defines its exact location in space. The position of a body in motion changes, of course. Therefore it is of interest to us where exactly the body is positioned at the beginning of its motion, during its course and at its end. Position of athletes in space is important because for example tactics in many sport games is based on the opponent’s position. We can present here a simple example of an athlete’s motion in space.

In many sports it is necessary to describe motion along a plane or even in three-dimensional space. Let us start with a two-dimensional situation. Imagine a football match where we need to describe the position of a penalty executor in the moment of his shooting at the goal (Fig. 7). The width of a football pitch is 48 m and the penalty spot is 11 m from the goal line. We can describe the position of the penalty executor in relation to the corner flag to the left from the goal keeper. We will thus consider the corner flag to be the zero point. Therefore the penalty executor is 11 m from the goal line and 24 m from the touch line.

Figure 7 Football pitch as the system of Cartesian coordinates.

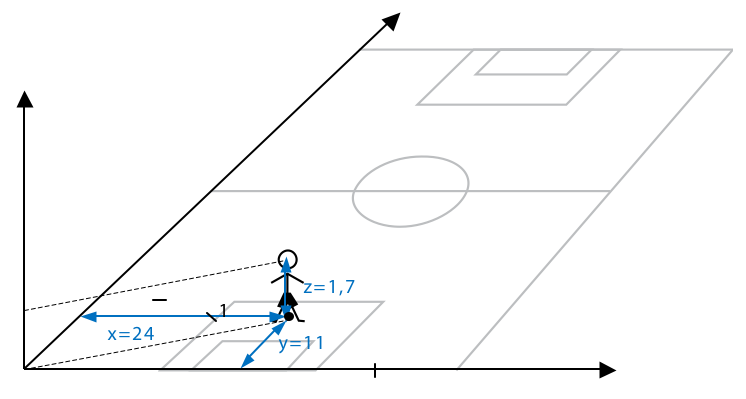
In this case the Cartesian system of coordinates with two axes (x and y) will help us. First we have to define the origin of the system of coordinates. In our case it is the corner flag to the left from the goal keeper. The touch line will be the y axis and the goal line will be the x axis. Positive values along the x and y axes are only determined within the playing field. Behind the goal line and behind the touch line to the left from the goal keeper the x and y values are negative. We will determine the position of the penalty executor with two coordinates (11 m; 24 m). In the case of three-dimensional space we would have to add the third coordinate, determining the position in the vertical direction. For example the head of the penalty executor is 1,7 m above the playing field so its position in our Cartesian system of coordinates would be (11 m; 24 m; 1,7 m).

In three-dimensional space we need three coordinates to describe the position of a body.

One coordinate of the Cartesian system of coordinates is vertical (z) and two coordinates are horizontal (x, y). The origin of the system of coordinates divides axes into their positive and negative halves. The unit of measurement used in describing position is length.