Kinetics

Moment of Force

Imagine you are in the gym taking exercise to strengthen your pectoral muscles or knee extensors on a special multipress. You set the load to 50 kg but soon you’ll find out that the resistance you feel also depends on the position of your leg on the arm of the given multipress. During the exercise the 50 kg load might sometimes seem to you as „half load“. Why is it so that we can lift heavy loads with a relatively small force?

This paradox can be explained by the concept of moment of force. Moment of force is the tendency of a force to twist or rotate an object. Motions of our extremities about our joints are caused by moments of force generated by our muscles. Thanks to muscles that produce moments of force in our joints we can move.

What is moment of force?

Moment of force is a measure of the force’s tendency to cause a body to rotate.

For example a gymnast on a horizontal bar will start to rotate only if he produces a relevant moment of force in relation to the horizontal bar. There are three kinds of situations in which an external force acts on a free body⁵²:

Central force – external force whose vector line⁵³goes through the centre of gravity of the body. Central force causes only linear motion. It is a force that acts on a bobsleigh in the straight part of the tracks⁵⁴.
Eccentric force⁵⁵ – external force whose vector line⁵⁶ does not go through the centre of gravity of the body. Eccentric force causes changes to both linear and rotary motion. The force acting on a gymnast at a moment of take-off in squat vault over the horse is a good example here.
Pair of forces – forces of identical magnitude but opposite direction, not lying in the same line. Such pairs of forces cause only changes in rotary motion. Resultant of these two forces is zero, therefore according to Newton’s first law these forces do not cause a change to linear motion.

Moment of force definition

The magnitude of the moment of force acting about a point⁵⁷ is directly proportional to the magnitude of the acting force and to the distance of this point from the vector line of the force that produces the moment. The distance between the vector line of the force and a selected point is called moment arm (Fig. 15).

Figure 15 Free body diagram – pole vault. Blue dot is the centre of gravity of the athlete. Black arrows represent reaction forces through which the pole acts on the athlete’s arms. Blue arrows represent moment arms in relation to the axis of rotation and the centre of gravity.

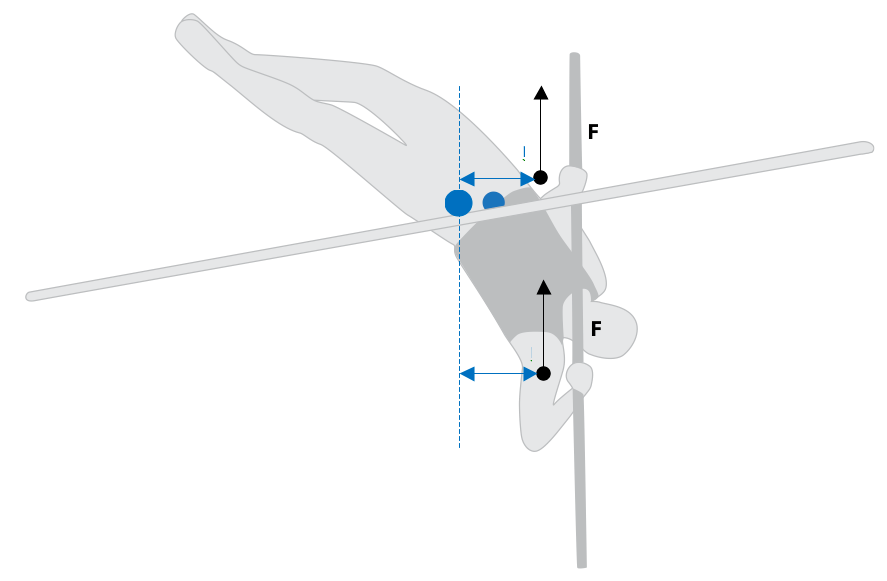
The following holds true: M = Fr, where M⁵⁸ is the magnitude of moment of force (N⋅m), F is the magnitude of force producing the moment (N), and r is moment arm (m).

Moment of force as a vector is defined with the help of the vector product of position vector r⁵⁹ and force F:

To fully describe moment of force we need to know the magnitude, direction, and the point of application of the force that produces momentum and we have to choose a moment point. If the vector of force lies on a plane that is perpendicular to the axis of rotation of the body, it is useful to choose as a moment point the point of intersection of this plane and the axis of rotation.

Examples of using moment of force in sport

When paddling in a kayak or a canoe we use a paddle. It is very important to carefully choose the position where we hold the paddle. Holding the paddle in various positions means various moments of force in driving and navigating the boat. As the point of rotation is where we hold the paddle with our top arm, the lower we put our bottom arm the bigger the moment of force is. It practically means that our strokes will be longer but with higher rotating effect of the same force of stroke. For example when we teach beginners to paddle it is necessary to make sure their bottom arm is low enough to enable them to navigate the boat despite using less force.

In tennis, golf, ice hockey, etc. moment of force depends on the way we hold the racket, golf club, ice hockey stick, etc. The correct grip is a necessity. But the correct grip may vary depending on the needs of a specific athlete in a specific situation. Moment of force must also be used in sports where either the athlete or the equipment he/she uses rotates. In martial arts, such as judo or Greco-Roman wrestling, athletes choose holds to produce highest possible moment of force.

Moment of muscle force

The above mentioned examples of moments of force in sport were all examples of external moments of force acting on a human body or on sport equipment. What causes our arms and legs to rotate about joints? Muscles produce moments of force that rotate our arms and legs. Muscles produce forces that act on insertions and subsequently on skeleton. In Fig. 16 we can see a force produced by biceps brachii on forearm when the position of elbow joint changes from full extension to 90° flexion. Do muscles always produce the same moment of force during that motion? The ability of biceps brachii to produce moment of force in elbow joint depends on the position of elbow joint. Moment arm of muscle force varies depending on the mutual position of the individual segments of the joint (Fig. 16). A change to the angle of the joint causes a change to the moment arm of muscle force. This fact partially explains why our muscles are able to produce substantially greater moments of force in certain positions compared to other positions in which moments of force produced by the same muscles are much smaller.

Figure 16 Moment arm of muscle force of biceps brachii decreases from r₁ to r₂ during extension in elbow joint. The centre of rotation of the elbow joint is marked with the white dot. Insertion of biceps brachii is marked with black dot in 90° position and blue dot in 120° position. The arrows mark forces by which the insertion of biceps brachii acts on tuberosities of radius and on bicipital aponeurosis of deep fascia on medial section of forearm.

Forces and moments of force in static balance

To keep a body in static balance the sum of external forces and the sum of external moments of force acting on that body must be zero.

Therefore the following must hold true:

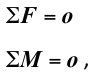
Estimate of muscle forces with the help of the equations of static balance

Are we able to know the forces by which individual muscles act on insertions and subsequently on bones when, for example, we lift a barbell? Imagine we are holding a 30kg barbell. Our elbow joint is in 90° flexion and our forearm is parallel with the floor. If the length of our forearm is 0.4 m, with what moment will the barbell act on our forearm in relation to the axis of rotation (elbow joint)?

The barbell will produce moment of force acting on our forearm with the magnitude of 118 N⋅m clockwise from our point of view. Let us mark clockwise direction of rotation as negative. In order to hold the barbell, elbow flexors must produce moment of force with the same magnitude as that of the barbell but with opposite direction – counter clockwise in our case. If elbow flexors are fixed approximately 0.03 m from the axis of elbow joint on the forearm, the following holds true:

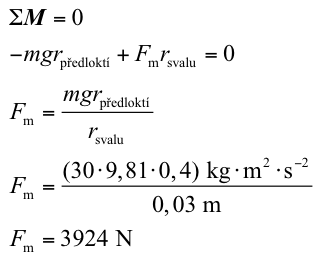
Elbow flexors must produce force with the magnitude of almost 4,000 N to hold a 30kg barbell! This means that our muscles must produce relatively great forces to produce effective moments in our joints because their moment arm is often quite short. The good point is that to produce effective moments it is enough for our muscles to only slightly contract (shorten).

Centre of Gravity

Centre of gravity is an imaginary point in a body where the total weight of the body may be thought to be concentrated⁶⁰. The concept of centre of gravity helps us to imagine motions of athletes and their equipment. It replaces real motions of human body because human body has a complicated shape and, moreover, this shape keeps changing during the motion. Such simplification of a complex body to just one point helps us to better understand real motions of human body and other objects.

In the centre of gravity the total weight of the body may be thought to be concentrated because it is the point of application of gravitational force of given body.

Centre of gravity is the point around which all gravitational forces acting on all individual points of the body are perfectly balanced. Centre of gravity is therefore the point of balance. What does it mean? Our body, for example, is composed of individual segments, such as head, upper arm, forearm, hand, trunk, thigh, shin, and foot. Human body can be imagined in a simplified way as a model of fourteen segments. Gravitational force acts on each of these fourteen segments. These gravitational forces acting on individual segments produce moments of force whose vector sum, in relation to the body’s centre of gravity, is zero. In the centre of gravity our body is in balance. But non-zero moments of gravitational force are produced in relation to all other points in human body and human body (or any object) is thus not in balance.

Centre of gravity is a point around which the gravitational force of mass elements of a body (e.g. of human body segments) is perfectly balanced.

Determination of centre of gravity in human body

If we know the gravitational force acting on individual segments and their position in relation to the origin of the chosen frame of reference, we can calculate the centre of gravity as:

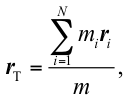
where r_T is the position vector of the body’s centre of gravity, r_i is the position vector of the i^th segment, m_i is the mass of the i^th segment, mis the mass of the body, and N is the number of segments⁶¹.

The above relation can be rewritten into a coordinate form:

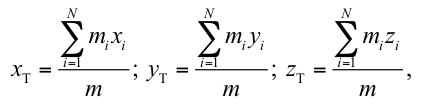
where x_T, y_T, z_T are coordinates of the body’s centre of gravity and x_i, y_i, z_i are coordinates of the centres of gravity of individual body segments.

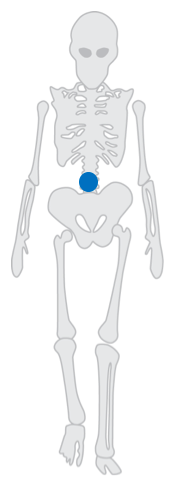
As we already know, human body is not a perfectly rigid body and thus the position of centre of gravity depends on the positions of individual segments. Let us imagine we are standing in the basic anatomical position. Sagittal plane divides the body into right and left sections. Because human body is almost symmetrical in relation to sagittal plane, the centre of gravity will be placed very near this plane. If we lift our right arm, the centre of gravity will shift to the right and up. Even though human body is not symmetrical in sagittal direction, the centre of gravity is somewhere on a frontal plane that divides the body into front and back sections. This plane goes approximately through shoulders and hips, and then slightly in front of anklebones. If we stretch our arms forward, the centre of gravity will shift forward, too. It is much more difficult to estimate the position of the centre of gravity in vertical plane. In basic anatomical position the centre of gravity lies in the area of the 3^rd to 4^th sacral vertebra.

Figure 17 Centre of gravity of human body when walking (blue).

Women have centre of gravity vertically lower than men because their bodies are bigger in the area of pelvis but their shoulders are narrower. The position of centre of gravity in women is in the relative height of 55 % of the total height, while in men it is 57 %. In children the position of centre of gravity is relatively higher compared to adults because children have relatively bigger head and shorter legs than adults.

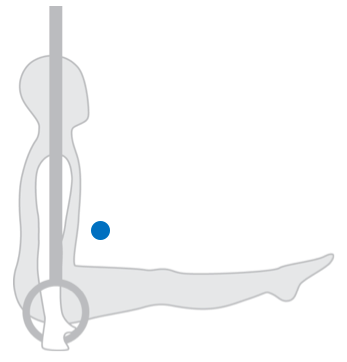
Figure 18 Centre of gravity does not have to lie inside human body. Centre of gravity of the gymnast below is marked with a blue dot.

Concept of centre of gravity and its use in performance improvement

Now we can think about how motion of our body segments influences our motor skills and performance by means of changing the position of centre of gravity. If we jump up in the air and lose contact with the floor, only gravitational force acts on us and we become a projectile. Under the effect of gravitational force from the moment of our take-off our centre of gravity is uniformly accelerating downwards (9,81 m/s²). At the beginning of our jump our centre of gravity has maximum velocity and, under the effect of gravitational force, it gradually slows down until it stops at the maximum height of the jump. Motion of our arms and legs cannot influence the motion of centre of gravity because we do not touch other bodies and cannot produce contact forces. The resultant force acting on us is still only gravitational force. The trajectory of our body’s centre of gravity cannot be influenced by our moving arms and legs but the motions of individual arms and legs influence each other. So for example if we bend our knees during the jump, the height of arms is reduced so that centre of gravity still moves along the same trajectory, determined from the moment of moment of take-off⁶².

Basketball players, for example, when trying to block the ball, jump up with only one arm raised. The other arm and both legs are not bent and do not move in relation to trunk. Volleyball players would also jump highest with only one arm raised and their legs outstretched. Why, then, volleyball players, unlike basketball players, jump with both arms raised above their heads? The answer is simple. Basketball players know where the ball is heading and they are only trying to block the ball if it is heading into the basket. Volleyball players, however, have no way of knowing where the ball will be heading after the smash and therefore it is better for them to jump with both arms raised above their heads, to cover wider area above the net, although in this way they cannot jump as high as they would otherwise be able to.

When we look at some spectacular jumps of basketball players, figure skaters, dancers, gymnasts, etc., we can see that they sometimes seem to be suspended in the air. It is only an effect of relative motions of individual body segments toward each other. If, for example, a basketball player jumping under the basket bends his knees the trajectory of his centre of gravity is still parabolic but his arms and the ball will stay longer in the same height. This fact creates an illusion of flight because the ball in the player’s hands does not fall although his centre of gravity does.

How the position of centre of gravity influences the stability of human body?

The stability of a body is a measure of its ability to return to a position of equilibrium after being disturbed.

In many sports and human activities athletes, or people in general, do not want to be unbalanced from a certain stance or position. They want to be in the most stable position possible. Wrestlers try to maintain the most stable position in order not to be overturned by their opponents. Biathlonists, tennis players, basketball players, archers, they all need a stable position to perform their skills best. In some sports, on the other hand, success is determined by an ability to change certain position very fast. Sprinters at start need to leave their starting position soonest possible. Downhill skiers, tennis players serving, swimmers at start, football goal keepers, they all must be able to change their position fastest possible when the right moment comes. For this purpose they produce a preparatory position which is not very stable.

Factors influencing stability

Stability of bodies is influenced by the height of centre of gravity above the floor, the size of support area, and the mass of the body.

How can we explain by mechanics that it is these three factors that influence stability? We know that for a balanced body it holds true that the sum of all moments of force acting on that body must be zero. From that it follows:

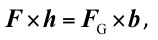
where F is the force trying to disturb the body from its balance, h is the moment arm, F_G is the gravitational force, and b is its moment arm.

Factors on the left side of the equation minimize the increase in stability, while factors on the right side of the equation maximize the increase in stability. This means that the higher the gravitational force of the body, the higher the moment of force on the right side of the equation and for that reason also the higher stability of the body. Prolonging the moment arm of gravitational force also increases stability. Length b is the horizontal distance of median⁶³ from the edge (point) of rotation. Stability of a body therefore depends on the direction of forces that try to disturb it. The height at which it is possible for a force to act on a body is taken as a share of the total height of that body. The higher the force F is acting, the higher the moment of force on the right side of the equation and therefore the chance of keeping stability is getting weaker.

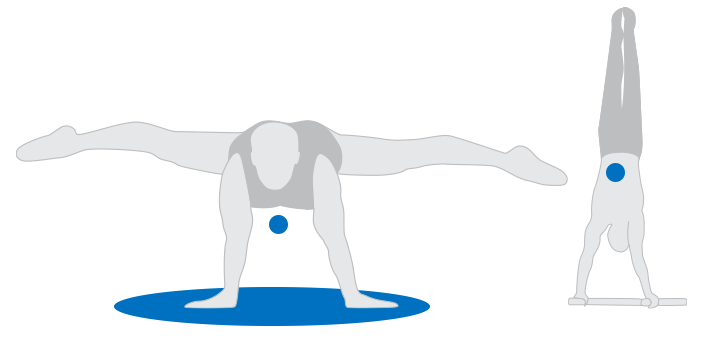
The fact that the height of the centre of gravity influences stability is better explained by the relation between work and potential energy. The most stable stance or position of a human body is the one with minimum potential energy. When an opponent tries to disturb us from a balanced position with minimum potential energy, he/she must perform more work than if we were in a position with more potential energy. The most stabile are those positions of human body that allow to place the centre of gravity below the point of rotation. Gymnast in a hanging position on a horizontal bar is a good example. If disturbed from balanced position, he gets back without having to perform any work. This is a stable equilibrium. On the other hand, when the centre of gravity is above the point of rotation, stability is lower (Fig. 19). Gymnast standing on his hands is a good example. If disturbed from balanced position, he will most probably tip over and will not get back into balanced position. His potential energy was too big because his centre of gravity was high above the point of rotation. This is an unstable equilibrium. In sport there are also examples of indifferent equilibrium. It is a specific situation when the axis of rotation goes through the centre of gravity. During rotation the potential energy of the body does not change. If a wrestler lies on the floor and spreads his arms and legs so that his centre of gravity is almost levelled with the floor, we can talk about indifferent equilibrium.

Figure 19 An unstable equilibrium. Centre of gravity (blue) is above the point of rotation.

Human motion, centre of gravity, and stability

Human body is not a solid body and its shape can change by moving arms, legs, head and trunk. Therefore people can control their stability by changing the position of their body.

For example, how do we start a step when walking? First we lean forward until our median reaches in front of our foot. Then we lose balance and start to fall over. The fall is broken by the other leg and the whole process is repeated again. Therefore we can describe walking as a series of controlled falls, landings and take-offs. In many sports athletes try to maximize their stability generally or only in one specific direction. In some sports we try in certain situations to maximize mobility (and minimize stability).

If the force that is trying to disturb us has a certain direction, we should make use of changing the base of our position to achieve greater stability. For example when playing forehand stroke tennis players try to put their feet far apart in the direction of the flying ball and thus to increase their front to back balance (Fig. 20). They stand sideways to the ball and one foot is in the direction of the stroke – their feet are not side by side. Similar technique is used by boxers and basketball players. The position with one foot in front is very favourable in many sporting situations. It allows to reduce or increase momentum and impact force in given time, but it also gives more stability.

Figure 20 Tennis players in certain phases of a stroke use a special position to maximise stability in the direction of the stroke.

In certain situations people increase their stability by using equipment. People with leg injuries often use crutches to increase their stability. Skiers increase their stability in front to back direction with the help of skis themselves. The longer the skis, the better the front to back stability. That is why downhillers use longer skis than slalom racers. They need better front to back stability. We often use short skis to practice funcarving. Short skis help instructors detect whether students have correct basic downhill skiing position. If a student starts to fall forward or backward during training with short skis, it is a sign of incorrect basic skiing position in the sense of front to back stability.

Sprinters at the start try to have a position that would allow them to move forward as fast as possible. The sprinter’s centre of gravity is in front of the toe of his front foot, around which the body will rotate during the first step. After the signal the sprinter rises his arms and immediately starts falling forward. He/she is stopped by the force of his/her legs. Swimmers similarly start from a position of minimum stability.

⁵² Free body has six degrees of freedom – its motion is not spatially limited.Zpět

⁵³ Vector line goes through the starting and the ending point of the vector of force.Zpět

⁵⁴ Bobsleigh is not a free body but nevertheless the effect of central force causes only linear motion.Zpět

⁵⁵ Eccentric in this case means a type of force, not a type of muscle contraction.Zpět

⁵⁶ Vector line goes through the starting and the ending point of the vector of force.Zpět

⁵⁷ Point to which moment of force is defined. It can lie on the axis of rotation, away from it, even away from the body itself.Zpět

⁵⁸ In English moment of force is also called torque and denoted with capital T. Zpět

⁵⁹ Also called radius vector.Zpět

⁶⁰ It is the point of application of resultant gravitational force, composed of all gravitational forces acting on all mass elements of the body.Zpět

⁶¹ If the chosen segments are head, trunk, left and right upper arm, left and right forearm, left and right hand, left and right thigh, left and right shin, and left and right foot, then N = 14.Zpět

⁶² If air resistance is neglected.Zpět

⁶³ Median is a line in which lies the vector of gravitational force. Therefore it goes through the centre of gravity and is vertical.Zpět