Fakulta sportovních studií Masarykovy univerzity
Mgr. Martina Bernaciková, Ph.D., Mgr. Miriam Kalichová, Ph.D., Mgr. Lenka Beránková, Ph.D.
Kinematika a dynamika lidského pohybu
Kinematická charakteristika pohybů člověka
Při lidském úmyslném pohybu dochází ke změnám poloh segmentů těla a těla jako celku v prostoru. Pohyby při sportovních činnostech jsou tedy v tomto smyslu změny polohy sportovce nebo částí jeho hmotné soustavy nebo jím způsobená změna polohy sportovního náčiní v čase. Na popis takovýchto složitých pohybových úkonů je potřeba jejich přesné určení. Kinematika je částí mechaniky, která se zabývá určováním polohy bodů a jejich změn v čase. Při této determinaci se nezabývá příčinami pohybu. Mezi veličiny, jimiž v rámci kinematiky pohyb popisujeme, patří dráha, rychlost, zrychlení. Kinematika tedy zkoumá pohyb z hlediska jeho průběhu v prostoru a v čase (Kovařík, Langer, 1994).
Pro optimální popis soustav pohybů byl zaveden pojem hmotný bod. Je to myšlený bod, kterým pro zjednodušení nahrazujeme těleso. Hmotný bod je umístěn v těžišti tělesa, jehož tvar a rozměry nejsou podstatné, avšak hmotnost tělesa se do hmotného bodu přenáší.
Pohyb a poloha těla a jeho částí je určován (vztahován) vzhledem ke zvolené vztažné soustavě. Vztažnou soustavou může být zemský povrch, ale také například určitý segment těla, ke kterému vztahujeme pohyb jiných segmentů. V trojrozměrném prostoru je poloha bodu jednoznačně určena třemi souřadnicemi. Nejpoužívanější je kartézská soustava souřadnic, kterou tvoří 3 osy na sebe kolmé s označením x, y, z.

Soustava souřadnic
K základním pojmům, které určují pohyb i polohu segmentů těla v prostoru a čase patří:
- Trajektorie – geometrická čára, po které se hmotný bod pohybuje
- Dráha – délka trajektorie
- Rychlost – vektorová veličina určující, jakým způsobem se mění poloha tělesa v čase
- Zrychlení - vektorová veličina určující, jakým způsobem se mění rychlost tělesa v čase
Při pohybech ve sportovních disciplínách nás často zajímá rychlost, se kterou sportovec, například při běhu na 100 metrů, a nebo výška, kterou dosáhne gymnasta při saltu. V tom okamžiku se hodnoty rychlosti a nebo výšky vztahuje i na těžiště těla a ne na jeho libovolnou část. Proto v mechanice musíme v těchto případech chápat tělo sportovce jako hmotný bod.
Dynamická charakteristika pohybů člověka
Na rozdíl od kinematiky, která popisuje pohyb v čase a v prostoru, aniž by zkoumala jeho příčiny, se právě dynamika zabývá příčinami změn pohybového stavu těla a jeho částí.
Síla jako příčina pohybu má mnoho forem. Jsou síly primární, které existují bez ohledu na konaný pohyb. K nim patří např. tíhová síla (FG), která neustále působí na každý segment lidského těla. Vliv gravitace na prováděný pohyb je různý v závislosti na charakteru pohybu. Jde-li o pohyb v směru působení gravitační síly, jsou její účinky urychlující, při pohybu v opačném směru má gravitační síla účinky brzdivé. Jsou však také síly, které vznikají teprve pohybem, jako odpor hmoty proti tomuto pohybu. To jsou síly sekundární, např. tření (FT). Těch je v oblasti sportovního pohybu převažující většina. Těmto silám říkáme vnější síly. Jiné síly vznikají v těle sportovce, např. svalová síla (FSV) nebo resistující síly pevnosti a pružnosti tělesných tkání. To jsou síly vnitřní. Všechny tyto síly mají vliv na pohyb lidského těla nebo do pohybu uvedeného náčiní. Někdy mohou být brzdou, jindy na správném průběhu pohybu spolupůsobí (Kovařík, Langer, 1994). Vedle reálných sil, které jsou projevem vzájemného působení těles, existují ještě zdánlivé neboli setrvačné síly. Tyto síly nemají svůj původ ve vzájemném silovém působení těles. Tyto síly vznikají jako důsledek zrychleného (zpomaleného) pohybu neinerciálních soustav. Setrvačné síly mají vždy tendenci udržet těleso v původním pohybovém stavu - v klidu při zrychlování pohybu, v pohybu při zpomalení pohybu.
Základem dynamiky jsou Newtonovy pohybové zákony – zákon setrvačnosti, zákon síly a zákon akce a reakce (neboli vzájemného působení těles).
Statická a dynamická rovnováha
Každý pohyb vychází z nějakého výchozího postoje – postury. Kračmar (2002) definuje posturu jako zaujetí polohy těla a jeho segmentů v klidu. Z fyzikálního hlediska se jedná o klidový stav, udržování polohy těla v klidové poloze je však dynamický proces kladoucí nároky na řídící mechanismy. Balatka (2002) chápe posturu jako dynamický proces udržování polohy těla a jeho částí ve stále se měnícím prostředí.

Postura při lyžování
Udržení těla a jeho částí v klidu vzhledem k dané vztažné soustavě je podmíněno úrovní statické rovnováhy. Z biomechanického hlediska je tělo v rovnovážné poloze, splňuje-li dvě následující podmínky:
výslednice F všech sil, které na těleso působí, je nulová. To matematicky vyjadřuje rovnice:
výsledný moment sil M (vzhledem k libovolné ose) působících na těleso je nulový, tedy:
O momentu síly mluvíme, jde-li o otáčivý pohyb těla nebo jeho částí kolem osy otáčení. Moment síly vyjadřuje otáčivý účinek působící síly.
Pro charakter rovnovážné polohy je podstatné, kde se nachází těžiště. Obecně platí, že rovnovážná poloha je tím stabilnější, čím se těžiště těla nachází níž. Pokud je tělo podepřeno pod těžištěm, je rovnováha ovlivněna také velikostí opěrné plochy. Proto je např. obtížnější udržet se ve výponu než ve stoji na celém chodidle.
Pokud tělo neudržujeme ve statické poloze, ale v pohybu, nahlížíme na jeho průběh jako na sled pohybových mikrofází. I v tomto případě mluvíme o rovnováze, ale o rovnováze dynamické. Tělo v průběhu pohybu přechází z jedné mikrofáze do druhé, tedy z jedné dynamické rovnováhy do druhé dynamické rovnováhy.
Pro dynamickou rovnováhu platí d´Alembertův princip. Ten říká, že součet rozdílů mezi silami působícími na systém a časovými změnami hybnosti systému při virtuálním posunutí systému (při započetí vazeb) je nulový. D´Alembertův princip bývá také formulován tak, že při pohybu mechanické soustavy jsou setrvačné cíly v rovnováze s explicitními silami.
Zjednodušeně řečeno platí, že výslednice sil je rovna nule. Na rozdíl od podmínky statické rovnováhy se však započítávají ještě setrvačné FS (neboli doplňkové) síly, které vznikají při zrychleném či zpomaleném pohybu a působí proti této změně pohybového stavu.
F1 + F2 + F3 + ... + Fn = 0
Totéž platí pro rovnováhu momentů sil. U dynamické rovnováhy započítáváme i momenty setrvačných sil MS.
M1 + M2 + M3 + ... + Mn = 0
Pákový systém kloubů
Systém kloubů kostí a svalů funguje jako pákový mechanismus, kdy osa otáčení prochází kloubem a kosti jsou ramena, na které působí svalové síly. Podle vzájemné polohy působící síly (svalové), břemene (tíhová síla) a osy otáčení rozeznáváme páky prvního, druhého a třetího stupně.
Páka prvního stupně (dvojzvratná) má osu otáčení mezi vektorem svalové síly a vektorem tíhové síly. Příkladem může být spojení lebky s páteří. Opěrným bodem je atlantookcipitální kloub. Ramenem síly (extenzorů hlavy) je vzdálenost opěrného bodu k vektoru této svalové síly, ramenem břemena je vzdálenost mezi opěrným bodem a vektorem tíhové síly hlavy. Při pohybu se poměr velikostí ramen neustále mění, což se projeví změnami momentů těchto sil.
Páka druhého stupně ( jednozvratná) má vektor břemena mezi opěrným bodem a vektorem působící svalové sily. Rameno síly je delší než rameno břemena. Příkladem je pohyb v hlezenním kloubu ve výponu. Bod otáčení je v metatarzofalangeálním kloubu. Břemenem je hmotnost těla, která působí ve směru těžnice blíže opěrnému bodu než vektor síly trojhlavého lýtkového svalu. Rameno tíhové síly je tak vždy menší než rameno síly svalové. Můžeme tedy konstatovat, že při izometrické kontrakci je svalová síla tolikrát menší než tíhová síla, kolikrát je rameno svalové síly větší než rameno síly tíhové.
Páka třetího stupně (jednozvratná) má rameno síly kratší než rameno břemena. Síla na této páce působí mezi opěrným bodem a břemenem. Většina kloubů patří právě mezi páky třetího stupně. Příkladem je flexe předloktí, kdy osa otáčení prochází loketním kloubem, břemenem je tíha předloktí a ruky, proti kterému působí na svém rameni síla dvojhlavého svalu paže. Vzhledem k poměru ramen sil je podmínkou izometrické kontrakce větší svalová síla než tíhová síla břemene.
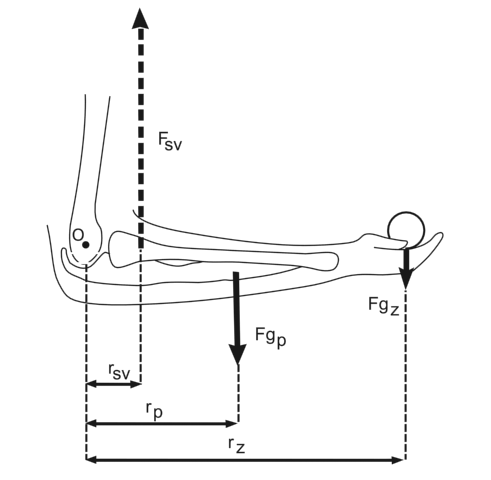
Pákový systém loketního kloubu (upraveno dle Nordin a kol., 2001)
Při flexi funguje loketní kloub jako páka 3. stupně. Tíhová síla segmentů předloktí a dlaně působící v jejich společném těžišti na rameni rP a tíhová síla zátěže FgZ působící na rameni rZ propínají loket. Tento otáčivý účinek je v opačném směru vyrovnán otáčivým účinkem svalové síly FSV (musculus biceps brachii), která působí na svém rameni rSV.
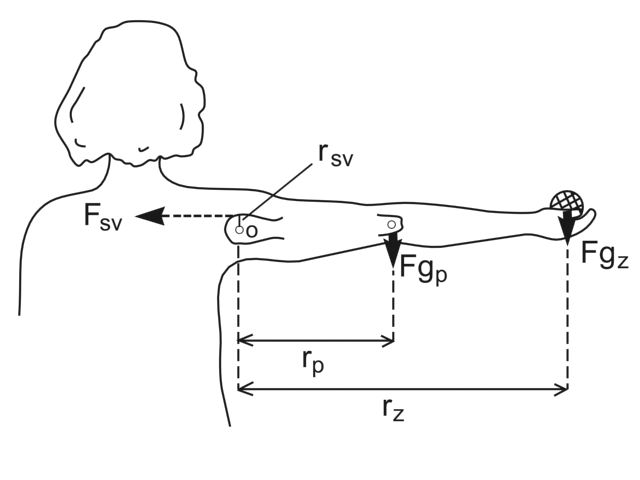
Pákový systém ramenního kloubu (upraveno dle Nordin a kol., 2001)
Při upažení působí ve směru addukce dvě síly - v těžišti paže tíhová síla segmentů paže FgP na rameni rP a tíhová síla FgZ zátěže, kterou člověk drží v dlani, na rameni rZ. Proti otáčivému účinku těchto sil působí svalová síla FSV (musculus deltoideus), jejíž rameno rSV je podstatně menší než ramena rP a rZ. Pro udržení horní končetiny v upažení musí platit ΣM = 0, tedy MFSV = MFGP + MFGZ.
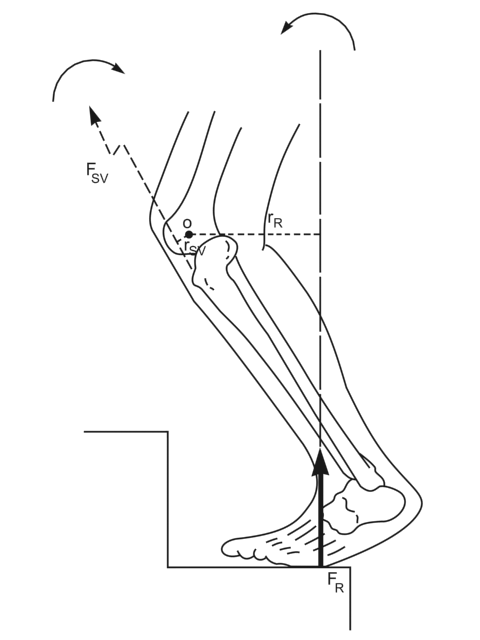
Pákový systém kolenního kloubu (upraveno dle Nordin a kol., 2001)
Obrázek představuje dva základní momenty sil aktivních při rotaci v kolenním kloubu při kontaktu chodidla s podložkou. Rotační moment způsobující flexi kolenního kloubu je moment síly FR – reakce podložky, která vzniká v důsledku tíhy těla. Tato síla působí na rameni rR. Opačný rotační účinek je vyvolán tahem svalu musculus quadriceps na rameni rSV. V rovnováze musí platit, že suma těchto dvou momentů sil MFR a MFSV je rovna nule (ΣM = 0).
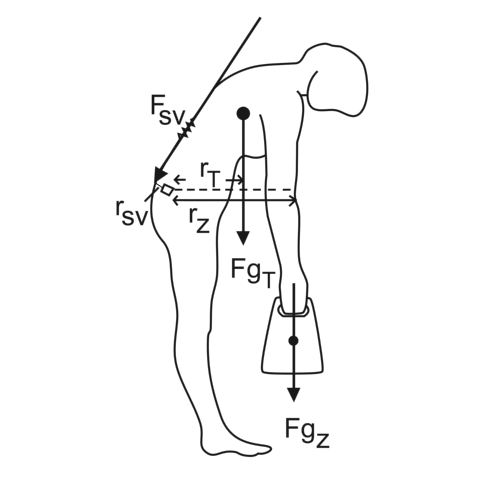
Silové působení při zatížení bederní ploténky (upraveno dle Nordin a kol., 2001)
Obrázek znázorňuje zatížení bederní ploténky při zvedání břemene. V předklonu působí tři základní síly – tíhová síla trupu FgT na rameni rT, tíhová síla zátěže FgZ na rameni rZ. Proti nim působí vzpřimovače trupu FSV na rameni rSV. Pro rovnováhu platí ΣM = 0, proto součet momentů sil, které ohýbají páteř do předklonu MFGT + MFGZ musí být v rovnováze s momentem svalové síly MFSV vzpřimující trup.
Mgr. Miriam Kalichová, Ph.D., Mgr. Lenka Beránková, Ph.D. |
Fakulta sportovních studií Masarykovy univerzity |
Návrat na úvodní stránku webu, přístupnost |
| Servisní středisko pro e-learning na MU, 2010
| Stránky střediska na Elportále
Technické řešení této výukové pomůcky je spolufinancováno Evropským sociálním fondem a státním rozpočtem České republiky.

