• 0. Úvod
• 1. Platón o uspořádání kosmu
• 2. Platón o duši
• 3. Platón o společnosti a státu
• 4. Platón o umění

Platón bez idejí

Když se řekne „počátky“ či „elementy“, rozumí se tím něco základního, prvotního, co samo už žádný další základ či počátek nemá. Je-li elementů více, pak také platí, že stojí na stejné úrovni, jsou na sobě nezávislé a odlišují se podstatnými vlastnostmi.

Viděli jsme, že čtyři tradiční elementy jsou podle Platóna takovým základem pro vše živé i neživé. Ukázali jsme (totiž jen naznačili, stejně jako sám Platón), jak je to „vše“ z elementů složeno. Mohlo by se tedy zdát, že zbývá popsat vlastnosti elementů a budeme mít tuto problematiku vyčerpánu.

Ovšem to bychom se nesměli zabývat Platónem. Platónem, který jakožto velký myslitel postoupil snad ve všech oblastech dále než jeho předchůdci a který byl natolik ovlivněn pýthagorejským viděním skutečnosti, že chtěl celý svět založit na matematických prvcích.

V „živlové teorii“ se Platónův postup projevuje geometrickým založením čtyř elementů, tedy nalezením jejich společného základu. Ale – není tím narušena elementárnost elementů? Nepopírá se tím úvodní vyjádření této kapitolky?

Na první pohled se zdá, že pokus najít základy základů je vlastně metodickou chybou – označujeme za základ něco, co ve skutečnosti základem není. Avšak celá věc nemusí být tak jednoduchá. Můžeme uvést příklad z moderní vědy, jenž Platónův postup ospravedlňuje.

S malým zjednodušením platí, že elementy z hlediska chemie najdeme v periodické soustavě prvků, chemie se pak – stále zjednodušujeme – zabývá vzájemnými interakcemi atomů jednotlivých prvků. Fyzika ovšem tyto atomy dále rozebírá, až dospěje k podstatně menšímu počtu elementů – elementárním částicím (leptonům, kvarkům a částicím zprostředkujícím silové působení).

Podobně lze chápat Platónův postup. Z hlediska fyzikálního lze rozlišit čtyři elementy – živly. Ovšem tyto živly samotné lze z hlediska jiné disciplíny dále analyzovat a nalézt jejich společné základy. Takovou disciplínou je pro Platóna geometrie.

Než osvětlíme tohle další zarážející tvrzení, vyložíme věc samotnou. Jak tedy jsou založeny elementy na geometrické rovině?

Elementy = pravidelná tělesa

Existuje pět pravidelných těles (běžně nazývaných také přímo „platónskými tělesy“), tj. těles, jejichž plochy jsou tvořeny shodnými mnohoúhelníky a z jejichž vrcholů vychází vždy stejný počet hran: čtyřstěn (z řečtiny tetraedr), šestistěn (krychle, hexaedr), osmistěn (oktaedr), dvanáctistěn (dodekaedr) a dvacetistěn (ikosaedr). O čtyřech živlech Platón tvrdí (viz Tim. 55d-56c), že každému z nich náleží jeden z těchto tvarů, tj. že každý z nich je tvořen velmi malými pravidelnými tělesy jednoho druhu. Přiřazení se děje především na základě kritéria pohyblivosti (či naopak stability) a dále na základě „ostrosti“ (jíž se rozumí schopnost působit rozrušení jiných živlů):

šestistěn - nejstabilnější, nejméně pohyblivý

země

čtyřstěn - nejpohyblivější, nejmenší (co do počtu ploch), nejostřejší		oheň
osmistěn - méně pohyblivý, větší, méně ostrý		vzduch
dvacetistěn - co do pohyblivosti mezi vzduchem a zemí, největší, méně ostrý než vzduch		voda

(Všechny obrázky v tomto oddíle © Michal Peichl, 2012.)

Dvanáctistěn přišel zkrátka, Platón nezavádí pátý živel. Proto mu poměrně neurčitě připisuje jinou funkci - prý byl užit při utváření celku kosmu (55c). Snad se tím naznačuje souvislost s dvanácti souhvězdími zvířetníku. Podle moderních badatelů také dvanáctistěn nejvíce ze všech pěti pravidelných těles připomíná kouli, jež je tvarem celého kosmu.

Jaký je fyzikální význam takového přiřazení? Naznačíme jen stručně. Krychle (pro jednoduchost uvažujme jen stejně velké) lze srovnat těsně k sobě, bez mezer a výsledné uspořádání bude stabilní, samo od sebe se nebude pohybovat. Stejně bez působení jiných živlů (především vzduchu – větru – a vody) zůstává na místě a beze změny země.

Zato čtyřstěn má velmi ostré hrany (a je menší, tedy i pronikavější než o něco méně ostrý osmistěn), jimiž může „řezat“ jiné živly, vnikat do nich, rozlučovat jejich tělesa od sebe, a tím podstatu živlů ničit, jako to dělá fyzikální oheň. Vzduch jako osmistěn a voda jako dvacetistěn jsou z hlediska těchto vlastností mezi ohněm a zemí.

Živly jsou tedy tvořeny pravidelnými tělesy. Ale kde jsou slibované společné základy základů? Dobrá otázka, Platónova úvaha totiž vede ještě dále.

Trojúhelníky – skladebné prvky těles

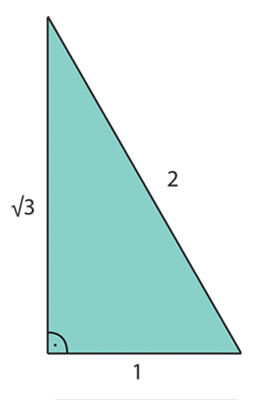
Pravidelná tělesa, jež tvoří živly, mají plochy tvořené trojúhelníky a právě ty jsou posledním skladebným základem smyslově vnímatelné skutečnosti (55c-d). Protože výše uvedená pravidelná tělesa se skládají ze dvou různých typů stěn – rovnostranného trojúhelníku a čtverce – potřebuje Platón jako základ dva rozdílné trojúhelníky.

Oba jsou pravoúhlé, jeden z nich navíc rovnoramenný, druhý je polovinou trojúhelníka rovnostranného. Z nich jsou pak seskládány plochy čtyř pravidelných těles následujícím způsobem:

Nyní jsou zřejmé dvě věci:

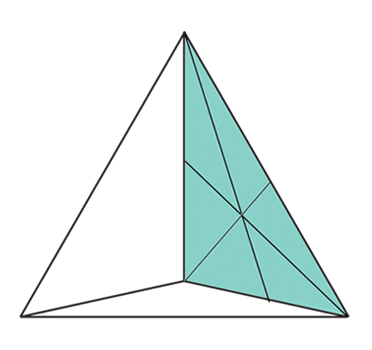1. Tři ze živlů jsou tvořeny druhým trojúhelníkem – oheň (čtyřstěn), vzduch (osmistěn) a voda (dvacetistěn). Navíc mají totožné plochy, což Platónovi umožňuje vysvětlit jejich vzájemné přechody.
   Ty jsou dány jednoduše poměrem ploch a předpokladem (obsaženým v pasáži 56d-57a), že jednotlivé tvary mohou být působením okolí, tedy jiných těles, např. „řezáním“ ostrým ohněm, rozloučeny na jednotlivé plochy, které se pak seskládají v jiné těleso. Nejjednodušší příklad – z jednoho osmistěnu vzduchu vzniknou dva čtyřstěny ohně. Složitější přechod – z jednoho dvacetistěnu vody vzniknou dva osmistěny vzduchu a jeden čtyřstěn ohně.
   Samotný proces „rozřezání“ či rozdělení těles nebo naopak spojování není nijak blíže popsán – můžete sami přemýšlet, co vše by bylo třeba vysvětlit.
   Zajímavý důsledek skládání těles ze dvou typů trojúhelníků však představuje určitá izolovanost země (naznačená i jejím oddělením v přehledu výše). Ta se totiž nemůže měnit v žádný jiný živel, jelikož je ohraničena plochami odlišných trojúhelníků.
2. Dvanáctistěn je tvořen pravidelnými pětiúhelníkovými plochami, jež nelze vytvořit ze dvou zvolených (a „nejdokonalejších“) trojúhelníků. Nemůže tedy být převeden na stejný základ, a to je důvodem jeho vyloučení z úvahy o živlech.

Ovšem po těchto dílčích vyjasněních je třeba vyjasnit nejdůležitější věc:

Proč trojúhelníky?

Nebo jinak formulováno – proč Platón hledá poslední základy fyzického světa právě v geometrii?

Geometrii spolu s aritmetikou, hudbou a astronomií (poslední dvě pojaty v kvantitativní, „aritmetické“ rovině) označil Platón už v sedmé knize Ústavy (R. 524e-531c) za disciplíny nezbytné na cestě k nejvyššímu poznání. Jejich zásluha spočívá v tom, že poznávajícího odvádějí od smyslové skutečnosti k pravému jsoucnu, smyslově nevnímatelnému – ovšem zde už překračujeme vymezení našeho kurzu, proto rychle zpět.

Ani tento „studijní plán“ z Ústavy není ještě úplnou odpovědí na položenou otázku, protože se netýká přímo vztahu geometrie a fyziky. Více se dozvíme ze samotného Tímaia, kde je celý výklad o geometrickém základu živlů uveden slovy:

Předtím tedy všechno toto bylo bez rozumného řádu a míry; když však bůh se jal pořádati vesmír, tu nejprve určitě odlišil tvary a čísly oheň, vodu, zemi a vzduch, které předtím měly sice jakési stopy své vlastní podstaty, ale celkem přece byly v takovém stavu, v jakém jest přirozeně všechno, kdykoli jest od něčeho vzdálen bůh. To pak, že bůh je vytvářel pokud možno nejkrásněji a nejlépe, kdežto dříve takové nebyly, budiž nám jednou pro vždy při všem podkladem...
Tim. 53a-b (zvýraznění J. P.)

Vlastně je to velmi prosté. Geometrie a aritmetika jsou přesné disciplíny, jež dokáží své předměty uchopit bez jakékoli nejasnosti, nejednoznačnosti, bez „rozmazanosti“ (srovnejte rozdíl mezi vlastnostmi „vysoký 185 cm“ a třeba „modrozelený“). Proto právě matematický výklad mohl být pro Platóna výrazem řádu skutečnosti. Dokonce by tvrdil, že jen to, co je uspořádáno na matematických základech, obsahuje řád. Jestliže pak byl přesvědčen, že v materiálním světě navzdory jeho proměnlivosti a nestálosti spatřuje řád, tedy něco vymezeného, pravidelného a stálého, byl vnitřně nucen nalézt nebo stanovit matematický základ látkové skutečnosti.

Přesvědčení o matematické podstatě řádu jako takového se zrcadlí i v Platónově požadavku na uspořádání lidského života podle čísla:

... vůbec jest uznati, že dělení a střídání čísel je ke všemu užitečné, i pokud se čísla střídají sama mezi sebou i pokud to je střídání v délkách a v hloubkách a také v tónech a v pohybech, jednak přímých ve směru sem a tam, jednak točivých kolem dokola. Se zřením na toto všechno má zákonodárce přikazovat všechno občanům, aby se neuchylovali od tohoto číselného řádu.
Zákony V, 747a

Autor Epinomidy pak doplňuje (Epin. 976d-977b), že znalost čísla jako nejvyšší moudrost a nejdůležitější nauka pochází z pozorování pohybů nebeských těles.

Ve fascinaci přesností matematiky a jasností uspořádanosti založené na matematických vztazích můžeme vidět Platónovu vědomou a často i explicitní (viz např. Ústava 530d) návaznost na pýthagorejce.

Geometrie a fyzika?

Moderní fyzika i chemie se zabývají empirickými skutečnostmi, proto tvrzení, že fyzika nachází základy chemických prvků, nepřináší žádný zásadní problém. Ovšem geometrie je na rozdíl od fyziky disciplínou abstraktní, čehož si byl velmi dobře vědom i Platón, který právě tuto skutečnost považoval za přednost geometrie – nezabývá se proměnlivým jsoucnem látkovým, nýbrž skutečným a neměnným. Jenže pak analogické tvrzení, totiž že geometrie vysvětluje podstatu fyzikálních elementů, zásadní problémy obsahuje.

Na zřejmě nejvýznamnější z nich upozornil už Aristotelés v první kapitole třetí knihy spisu O nebi (De cael. 299a2-300a19). Jeho úvahu můžeme shrnout následovně:

• Budeme-li tvrdit, že se tělesa skládají z ploch, pak musíme přijmout i tvrzení, že plochy se skládají z čar a čáry z bodů.
• Ovšem body nemají žádnou tíži, tedy ji nemohou mít ani čáry, ani plochy.
• Pak ani spojením jakéhokoli počtu ploch nevznikne těleso, jež by mělo byť sebemenší tíži.
• Jak tedy vysvětlíme, že elementy se tíží liší (což Platón výslovně uvádí)?

Obecně se pak tyto problémy týkají otázky, jak čistě geometrické plochy mohou vytvořit tělesa se smyslově vnímatelnými, „látkovými“ vlastnostmi (viz opět Aristotelés, O vzniku a zániku I 2, 316a). Platón by se zřejmě hájil tím, že tyto vlastnosti nenáležejí samotným geometrickým tělesům, nýbrž teprve jejich shlukům (viz např. vysvětlení měkkosti a tvrdosti v Tim. 62b-c), přesto se vnucuje pochybnost, že by abstraktní geometrické plochy byly s to zapříčinit všechny vlastnosti fyzikální. (Objevuje se i názor – P. Kalkavage, že vysvětlení živlů pomocí geometrických těles je spíše geometrická metafora a analogie než doslovně míněná teorie.)

Jestliže tyto komplikace Platóna neodradily od geometrického výkladu, tím výrazněji se vyjevuje jeho pýthagorizující přesvědčení o pevném a neměnném řádu v proměnlivé látkové skutečnosti, který vychází z matematické přesnosti skutečnosti nadsmyslové, inteligibilní.