4. Pravděpodobnost v genetické analýze a předpovědi
Příklad 1
Fenylketonurie (PKU) je dědičná choroba u člověka, při které lidské tělo není schopno odbourávat aminokyselinu fenylalanin, která je součástí bílkovin v potravě. Choroba se projevuje v raném věku dítěte a není-li léčena, vede k mentální retardaci. PKU se dědí jako recesivní znak.
Mladý pár chce mít první dítě. Muž má sestru a žena bratra, kteří mají tuto chorobu. Další případy nejsou v rodinách známé. Jaká je pravděpodobnost, že jejich první dítě bude postižené PKU?
Pravděpodobnost, že první dítě bude postižené PKU je %
Vzorové řešení
| P: | zdravý muž, jehož sestra je nemocná | x | zdravá žena, jejíž bratr je nemocný |
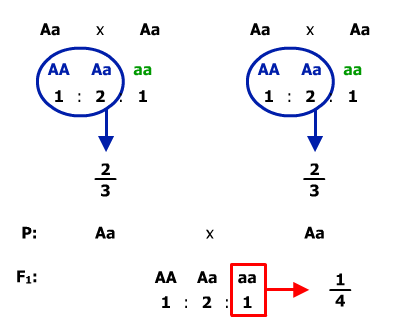
Z uvedeného vyplývá, že rodiče obou jedinců byli heterozygotní, protože sami byli zdravý, ale měli postiženého potomka (zeleně), sourozence sledovaných jedinců (viz. obrázek). Aby se dvěma jedincům mohlo narodit recesivně postižené dítě, musí být oba zdravý rodiče heterozygotní. To znamená, že uvažujeme pouze situaci, že oba rodiče, kteří se takto sejdou jsou heterozygoti. Četnost takových heterozygotních jedinců v potomstvu je 2/3 (uvažujeme podíl heterozygotů jen ze zdravých jedinců (jen z modrých), protože víme, že oba jedinci ve sňatku jsou zdraví (viz. zadání). Pravděpodobnost, že se tito dva jedinci potkají je tedy 2/3 x 2/3. Pravděpodobnost, že se dvěma heterozygotům narodí recesivně homozygotní potomek je 1/4.
Výslednou pravděpodobnost, že se tedy narodí dvěma uvedeným jedincům jako první postižené dítě zjistíme jako 2/3 x 2/3 x 1/4 = 1/9. Riziko je tedy pro uvedené rodiče asi 11 %.
Příklad 2
Onemocnění galaktosemie se dědí jako autozomální recesivní znak. Zdravá dvojice má postižené dítě.
Jaká je pravděpodobnost, že nastanou následující situace:
-
Následující 2 děti budou mít galaktosemii.
Pravděpodobnost je / .
Vzorové řešení
P: Gg x Gg F1: gg 1/4 x 1/4 = 1/16
-
Z následujících čtyř dětí bude mít 1 galaktosemii.
Pravděpodobnost je / .
Vzorové řešení
(4! / 3! x 1!) (3/4)3 (1/4) = 27/64
-
Otec dítěte s galaktosemií je heterozygotní ve sledovaném znaku.
Pravděpodobnost je %.
Vzorové řešení
P: Gg x Gg F1: gg Pravděpodobnost je 100%.
-
Babička z otcovy strany je heterozygotní ve sledovaném znaku.
Pravděpodobnost je / .
Vzorové řešení
Pravděpodobnost je 1/2.
-
Dítě, které má zdravý sourozenec nemocného dítěte bude heterozygotní ve sledovaném znaku.
Pravděpodobnost je / .
Vzorové řešení
Aby zdravý sourozenec mohl mít heterozygotního potomka, pak sám musí být heterozygotní. Protože víme, že je zdravý, pak podíl takových jedinců je 2/3 a tedy pravděpodobnost, že zdravý sourozenec nemocného dítěte je heterozygot, jsou ony 2/3. Dále předpokládáme, že si vezme zdravého muže nebo ženu, tedy dominantního homozygota. Podíl heterozygotních potomků ve sňatku heterozygotního jedince a dominantně homozygotního partnera je 1/2. (Totéž platí i za předpokladu, že tento druhý partner bude heterozygot či snad recesivní homozygot)
Tedy pravděpodobnost, že dítě, které má zdravý sourozenec nemocného dítěte, bude heterozygotní ve sledovaném znaku je 2/3 x 1/2 = 1/3.
-
Jakýkoli potomek bude nemocný.
Pravděpodobnost je / .
Vzorové řešení
P: Gg x Gg F1: gg Pravděpodobnost je 1/4.
-
Nevyskytne se žádný nemocný potomek u 3 následujících potomků.
Pravděpodobnost je / .
Vzorové řešení
(3/4)3 = 27/64
-
Mezi 3 následujícími dětmi budou 2 heterozygotní a další dominantně homozygotní.
Pravděpodobnost je / .
Vzorové řešení
(3! / 2!) (1/2)2 (1/4) = 3/16
-
Pravděpodobnost, že jakékoli dítě bude:
dívka s galaktosemií: / .
zdravý chlapec: / .
Vzorové řešení
P: Gg x Gg F1: gg Pravděpodobnost, že jakékoliv dítě bude dívka s galaktosemií je
1/2 x 1/4 = 1/8.Pravděpodobnost, že jakékoliv dítě bude zdravý chlapec je
1/2 x 3/4 = 3/8. -
První dítě bude normální chlapec a druhé bude nemocná dívka.
Pravděpodobnost je / .
Vzorové řešení
P: Gg x Gg F1: gg (1/2 x 3/4) (1/2 x 1/4) = 3/64
-
V rodině se 4 dětmi budou alespoň 2 děti zdravé.
Pravděpodobnost je / .
Vzorové řešení
[6 (3/4)2 (1/4)2] + [4 (3/4)3 1/4] + (3/4)4 = 243/256
-
V rodině se 4 dětmi budou 2 nemocné dívky a 2 nemocní chlapci.
Pravděpodobnost je / .
Vzorové řešení
6 [(1/2 x 1/4)2 x (1/2 x 1/4)2] = 6/4096 = 3/2048
-
Z prvních 2 dětí budou obě nemocné nebo obě zdravé.
Pravděpodobnost je / .
Vzorové řešení
Obě nemocné: 1/4 x 1/4 = 1/16
Obě zdravé: 3/4 x 3/4 = 9/16
Tedy celkem: 1/16 + 9/16 = 10/16 = 5/8
Příklad 3
U člověka je hypotrichóza recesivní znak.
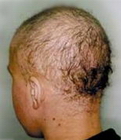 (Jeden z projevů hypotrichózy)
(Jeden z projevů hypotrichózy)
-
Zdraví rodiče mají 5 dětí, první 2 jsou nemocné a další jsou zdravé.
Genotyp rodičů je:
- genotyp muže
- genotyp ženy
Pravděpodobnost, že všechny zdravé děti jsou heterozygotní, je / .
Vzorové řešení
P: zdravý rodič
Aax zdravý rodič
AaF1: 2 děti nemocné,
aadalší 3 zdravé
A-Pravděpodobnost, že všechny zdravé děti jsou heterozygotní je
(2/3)3 = 8/27. -
Zdravý muž a nemocná žena mají 3 děti, 1 nemocné a 2 zdravé.
Genotyp muže je
Pravděpodobnost, že zdravé děti jsou heterozygotní, je %.
Jedno z těchto zdravých dětí si vezme zdravé dítě z př. a).
- pravděpodobnost narození nemocného dítěte, je / .
- pravděpodobnost, že ze 4 dětí budou všechny zdravé, je / .
Vzorové řešení
P: zdravý muž
Aax nemocná žena
aaF1: 1 dítě nemocné,
aa2 děti zdravé
Aa
Pravděpodobnost, že zdravé děti jsou heterozygotní je 100%.
Křížení:
P: zdravé dítě (příklad b)
Aax zdravé dítě (příklad a)
Aa (2/3)F1: aa (1/4)
Pravděpodobnost, že se zdravému dítěti z příkladu b) narodí ze sňatku s dítětem z příkladu a) nemocné dítě je 1 x 2/3 x 1/4 = 2/12 = 1/6.
Pravděpodobnost, že budou mít 4 děti a všechny zdravé je
1 x 2/3 x (3/4)4 = 162/768 = 81/384 = 27/128.
Příklad 4
Počty dívek a chlapců ve 240 rodinách, z nichž každá má 4 děti, jsou v následující tabulce.
| Počet chlapců | Počet dívek | Počet rodin |
| 0 | 4 | 12 |
| 1 | 3 | 69 |
| 2 | 2 | 84 |
| 3 | 1 | 57 |
| 4 | 0 | 18 |
Hodnota chí-testu, jímž jste ověřovali, zda jsou uvedené údaje ve shodě s předpokladem, že poměr pohlaví je 1:1, je (zaokrouhlete na 1 desetinné místo)
Jsou uvedené údaje ve shodě?
Vzorové řešení
Pro každý poměr pohlaví si spočítáme jaká je pravděpodobnost, že nastane takový stav a přepočítáme si ji do očekávaného počtu rodin. Pak pomocí chí-testu ověříme, zda údaje o počtech rodin s daným rozložením pohlaví u čtyřech dětí statisticky odpovídají očekáváním.
Poměr pohlaví má být 1:1, tedy
p = 1/2
q = 1/2
n = 4
| a) | 0 chlapců, 4 dívky s=0 t=4 |
b) | 1 chlapec, 3 dívky s=1 t=3 |
| (4! / 0! 4!) (1/2)4 = 1/16 x 240 = 15 rodin |
(4! / 1! 3!) (1/2) (1/2)3 = 1/4 x 240 = 60 rodin |
||
| c) | 2 chlapci, 2 dívky s=2 t=2 |
d) | 3 chlapci, 1 dívka s=3 t=1 |
| (4! / 2! 2!) (1/2)2 (1/2)2 = 3/8 x 240 = 90 rodin |
(4! / 3! 1!) (1/2)3 (1/2) = 60 rodin | ||
| e) | 4 chlapci, 0 dívek s=4 t=0 |
||
| (4! / 4! 0!) (1/2)4 = 15 rodin | |||
| Pozorované počty | 12 | 69 | 84 | 57 | 18 |
| Očekávané počty | 15 | 60 | 90 | 60 | 15 |
χ42 = (12-15)2/15 + (69-60)2/60 + ... = 3,1
Kritická hodnota pro 4 stupně volnosti na 5% hladině významnosti je 9,49. Hodnota chí-testu nepřekračuje tuto kritickou hodnotu a lze tedy říct, že zjištěné počty rodin s různým rozložením pohlaví u čtyř dětí odpovídají očekávání, a tedy že poměr pohlaví je opravdu 1:1. Z hlediska pravděpodobnosti tedy bude nejvíce rodin se čtyřmi dětmi takových, v nichž se narodí 2 chlapci a 2 děvčata.
tech. spolupráce: Servisní středisko pro podporu e-learningu na MU, Brno 2007