A.6 Anuloidová soustava

V tomto případě také nebudeme uvádět úplný popis všech vztahů a operátorů, i s ohledem na to, že daná soustava je příliš specifická, resp. týká se pouze jednoho typu geometrického tělesa, tzv. anuloidu (toroidu) – viz obrázek A.5 (popis soustavy rovněž odkazuje k příkladům 6.47 a 6.58). Ukážeme pouze, jak je možné flexibilně adaptovat principy, odvozené pro předchozí univerzální geometrické systémy na (v podstatě jakýkoli) speciální případ.

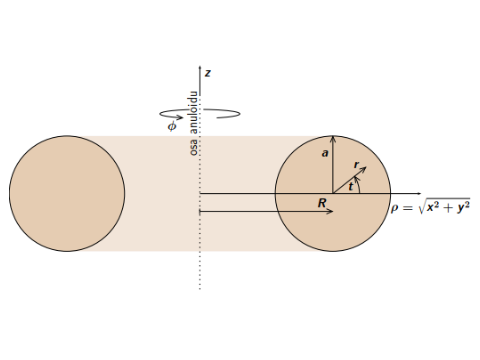
Obrázek A.5: Příčný řez anuloidem v rovině $\rho$-$z$, jednotlivé směry odpovídají válcové soustavě.
Animace vzniku anuloidu.

Statický obrázek — Obrázek A.5: Příčný řez anuloidem v rovině $\rho$-$z$, jednotlivé směry odpovídají válcové soustavě.
Animace vzniku anuloidu.

Anuloidem nazýváme těleso, které vznikne rotací kružnice okolo osy, která leží v rovině této kružnice a nemá s ní společný bod (vznikne tak válcově symetrická trubice - torus, připomínající duši pneumatiky).

Označíme-li $R$ poloměr osy toru, $a$ poloměr trubice (toru), $r$ radiální vzdálenost uvnitř trubice vzhledem k ose trubice, $t$ úhlovou souřadnici vnitřku trubice a značení ostatních směrů bude odpovídat standardní cylindrické notaci, tj. $\rho$ bude odpovídat radiální vzdálenosti od osy celého anuloidu, $\phi$ bude azimutální úhel anuloidu a $z$ vertikální souřadnice (vše je vyznačené v obrázku A.5), můžeme za anuloidové (proměnné) souřadnice považovat $r,\phi,t$ (v pravotočivém smyslu). Transformační vztahy můžeme zapsat následovně,

$$ x=(R+r\cos t)\cos\phi,\quad y=(R+r\cos t)\sin\phi,\quad z=r\sin t. $$

A.104

Vztahy pro zpětnou transformaci budou mít v tomto případě tvar

$$ r=\sqrt{\left(\sqrt{x^2+y^2}-R\right)^2+z^2},\quad\phi=\text{arctg}\,\dfrac{y}{x},\quad t=\arcsin\dfrac{z}{\sqrt{\left(\sqrt{x^2+y^2}-R\right)^2+z^2}}. $$

A.105

Kovariantní metrický tenzor $g_{ij}$ a příslušné Laméovy koeficienty anuloidové souřadné soustavy budou,

$$ g_{ij}= \begin{bmatrix} 1& 0 & 0\\0& (R+r\cos t)^2 & 0\\0 & 0 & r^2 \end{bmatrix},\quad h_r=1,\,h_\phi=R+r\cos t,\,h_t=r. $$

A.106

Vzhledem k tomu, že jde o diagonální metriku, bude kontravariantním metrickým tenzorem $g^{ij}$ zpětné transformace rovněž tenzor s převrácenými hodnotami prvků na hlavní diagonále. Jakobián souřadnicové transformace z kartézské do anuloidové soustavy tedy bude

$$ J=r(R+r\cos t), $$

A.107

jakobiánem zpětné transformace bude opět výraz $J^{-1}$. Ostatní parametry lze snadno odvodit analogickým způsobem jako v předchozích soustavách.