C.2 Interpolace a regrese
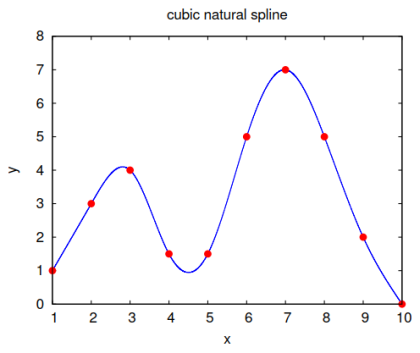
Interpolací rozumíme nahrazení složitější funkční závislosti závislostí jednodušší, tedy aproximace dané funkce jinou vhodnou funkcí. Interpolační aproximací rozumíme interpolaci diskrétní funkce, tj. funkce, dané konečným souborem bodů definičního oboru a jim přiřazených funkčních hodnot (reprezentovaných zpravidla tabulkou), pomocí funkce, nabývající v těchto bodech stejných hodnot jako původní zadaná funkce. Nejvhodnějšími interpolačními funkcemi jsou polynomy, např. tzv. Lagrangeův a Newtonův interpolační polynom (Humlíček, 2009; Vitásek, 1987) nebo tzv. splajny. V následujícím odstavci C.2.1 je stručně ukázán často používaný tzv. kubický interpolační splajn.
Regresí (regresní analýzou) nazýváme hledání takové funkce (tzv. regresní funkce), která nejlépe vystihuje vztah mezi dvěma skupinami proměnných, např. závislost náhodných veličin (naměřených hodnot) na čase, atd. Předem je dáno, která proměnná je nezávislá (vysvětlující nebo také regresor) a která je závislá (vysvětlovaná nebo také odezva). Jednoduchá regrese popisuje závislost odezvy na jednom regresoru, naproti tomu vícenásobná regrese popisuje situaci, kdy odezva závisí na více regresorech. Podle charakteru a průběhu zkoumané závislosti volíme typ regresního modelu, například lineární regresi (proložení závisle proměnných hodnot přímkou), regresi polynomem $n$-tého stupně, atd., a také nejvhodnější statistickou metodu, například metodu nejmenších čtverců nebo tzv. robustní regresi, která eliminuje extrémně vychýlené hodnoty, atd. (viz také pojmy a statistické metody, uvedené v kapitole 12 nebo například na stránkách http://physics.muni.cz/mikulas/zvc.html.
C.2.1 Kubický interpolační splajn
(z anglického spline) je jednou z nejčastěji používaných interpolačních funkcí. Jedná se o tzv. po částech (piecewise) interpolační polynom 3. stupně $s_i$ ve tvaru
definovaný jako
jehož druhé derivace označíme jako $M_i$. Je to tedy soustava kubických funkcí, které na sebe v zadaných bodech $[x_i,y_i]$ navazují jak funkční hodnotou, tak první a druhou derivací. Podle okrajových podmínek rozlišujeme různé typy těchto splajnů, například tzv. přirozený splajn je určen okrajovými podmínkami $M_1=M_n=0$, parabolický ukončený splajn je určen okrajovými podmínkami $M_1=M_2,\,M_n=M_{n-1}$ (extrapolace nultého řádu), kubický ukončený splajn je určen okrajovými podmínkami $M_1=2M_2-M_3,\,M_n=2M_{n-1}-M_{n-2}$ (extrapolace 1. řádu nebo také lineární extrapolace), atd.
Z podmínek spojitosti funkčních hodnot i prvních a druhých derivací v bodech $x_i$, vyplývá pro $i=0,\,\ldots\,,n-1$ následující:
| $s_i(x_i)=y_i$ | $s_i(x_{i+1})=y_{i+1},$ | (C.3) | |
| $s^\prime_{i-1}(x_i)=s^\prime_{i}(x_i)=c_i$ | $s^{\prime\prime}_{i-1}(x_i)=s^{\prime\prime}_{i}(x_i)=M_i=2b_i,$ | (C.4) |
tyto vnitřní podmínky jsou dále doplněny dvěma uvedenými okrajovými podmínkami, danými typem splajnu. Porovnáním všech uvedených podmínek ve všech uzlových bodech $[x_i,y_i]$ dostáváme soustavu lineárních rovnic pro neznámé druhé derivace $M_i$ ve vnitřních uzlových bodech:
Tuto soustavu rovnic lze zapsat pomocí tzv. tridiagonální matice ve tvaru (kde zavedeme $\Delta x_i=x_{i+1}-x_i$, $\Delta^+x_i=x_{i+1}-x_{i-1}$, $\Delta y_i=y_{i+1}-y_i$, $\Delta_j=\Delta y_j/\Delta x_j$, $\Delta_j^{\,i}=\Delta y_i/\Delta x_i-\Delta y_j/\Delta x_j$):
kterou řešíme například pomocí vhodné knihovny balíčku LAPACK (odstavec C.1). Jednotlivé koeficienty rovnice C.2 potom snadno dopočítáme:
V případě konstantního kroku nezávisle proměnné $x_{i+1}-x_i=h=\text{konst.}$ se rovnice C.5 zjednoduší do podoby
matice C.6 bude mít potom tvar
program nat3_splajn !deklarace názvu programu implicit none !příkaz, který ruší automatické přiřazování !písmen i, j, k, l, m, n pro celočíselné !proměnné a ostatních písmen pro reálné !proměnné (tj. proměnné s desetinným rozvojem) !tabulka hodnot $[x_i,y_i]$: ![1,1], [2,3], [3,4], [4;1,5], [5;1,5], [6,5], [7,7], [8,5], [9,2], [10,0] integer :: i, j, np !deklarace celočíselných proměnných: !i = pořadové číslo nezávisle proměnné, !j = pořadové číslo lineární rovnice, !np = celkový počet diskrétních hodnot. parameter (np=10) !zadání fixní hodnoty np, kterou nelze !v programu dále měnit! integer :: INFO,KL,KU,LDAB,LDB,N,RHS !deklarace celočíselných proměnných procedury LAPACK !– viz sekce C.1. parameter(KL=np-3,KU=np-3,N=np-2,KUKL=KL+KU+1,LDAB=2*KL+KU+1,& LDB=N,RHS=1) !zadání fixních hodnot celočíselných parametrů integer :: IPIV(N) !zadání parametru jako pole o N prvcích double precision, dimension(np) :: x, y !deklarace reálných veličin x, y jako pole (vektoru) !o np prvcích s tzv. dvojitou přesností, !umožňující výpočet čísla na 16 desetinných míst !a do mocniny cca 10300 (v závislosti na parametrech !počítače). double precision, dimension(np) :: M(N,N),AB(LDAB,N),B(LDB,RHS) !zadání parametrů jako dvojrozměrných polí double precision :: f(np), res(np), a(np), b(np), c(np), d(np) !jiný způsob deklarace reálných veličin jako !pole (vektoru) o np prvcích s dvojitou přesností. double precision :: h !deklarace reálných skalárních veličin. parameter (h=1.d0}) !zadání fixní hodnoty intervalu nezávisle proměnné, !kterou nelze v programu dále měnit! x=(/(1.d0*i, i=1,np)/) !vektor hodnot nezávisle proměnné. y=(/1.d0, 3.d0, 4.d0, 1.5d0, 1.5d0, 5.d0, 7.d0, 5.d0, 2.d0, 0.d0/) !y-ové (naměřené) hodnoty, !np = počet naměřených hodnot do i=1,N !cyklus výpočtu druhých derivací $M$, !zápis tridiagonální matice do j=1,N if(j.eq.i)then M(i,j)=4.d0 elseif(j.eq.i-1)then M(i,j)=1.d0 elseif(j.eq.i+1)then M(i,j)=1.d0 else M(i,j)=0.d0} endif end do end do do i=1,N !výpočetní cyklus procedury LAPACK do j=1,N AB(KUKL+i-j, j)=M(i,j) end do end do do i=1,N !výpočet pravé strany B(i,1)=6.d0}/h**2.d0}*(y(i)-2.d0}*y(i+1)+y(i+2)) end do !volání podprogramu DGBSV (viz oddíl C.1): call DGBSV(N,KL,KU,1,AB,LDAB,IPIV,B,N,INFO) if(INFO.ne.0) write(*,*) ``INFO='',INFO,``!!!'' a(1)=B(1,1)/6.d0/h !výpočet koeficientů a,b,c,d v 1. poli splajnu b(1)=0.d0} c(1)=(y(2)-y(1))/h-B(1,1)/6.d0*h d(1)=y(1) do i=2,np-2 !cyklus výpočtu koeficientů a,b,c,d !v prostředních polích splajnu a(i)=(B(i,1)-B(i-1,1))/6.d0/h b(i)=B(i-1,1)/2.d0 c(i)=(y(i+1)-y(i))/h-(B(i,1)+2.d0*B(i-1,1))/6.d0*h d(i)=y(i) end do a(np-1)=-B(N,1)/6.d0/h !výpočet koeficientů v posledním poli b(np-1)=B(N,1)/2.d0 c(np-1)=(y(np)-y(np-1))/h-2.d0}*B(N,1)/6.d0*h d(np-1)=y(np-1) do i=1,np-1 !zápis koeficientů do souboru fort.1 write(1,*) a(i), b(i), c(i), d(i) end do
C.2.2 Lineární regrese metodou nejmenších čtverců
Souborem $n$ diskrétních hodnot odezvy (vysvětlované proměnné) $y_i$, $i=1,\,\ldots\,,n$, který je určen výčtem uspořádaných dvojic $[x_i,y_i]$, proložíme přímku (polynom 1. stupně) $f^\text{I}(x)=kx+q$ tak, aby součet $S$ druhých mocnin tzv. reziduí, tj. vzdáleností bodů $y_i$ od funkčních hodnot $f(x_i)$ v bodech $x_i$ byl minimální (2. mocniny se zde používají kvůli nezávislosti na znaménku odchylky). Dostáváme tedy rovnici
pro dvě neznámé hodnoty $k$ a $q$. Minimalizaci této funkce provedeme položením $\partial S/\partial k=0$ a zároveň $\partial S/\partial q=0$, výsledek můžeme zapsat pomocí maticového formalismu jako
Snadno tak nalezneme výrazy pro oba hledané parametry v závislosti na uspořádané $n$-tici $[x_i,y_i]$ (např. na naměřených hodnotách v závislosti na čase nebo poloze),
Metodu navrhl a poprvé použil Karl Friedrich Gauss pro výpočet geodetických chyb.
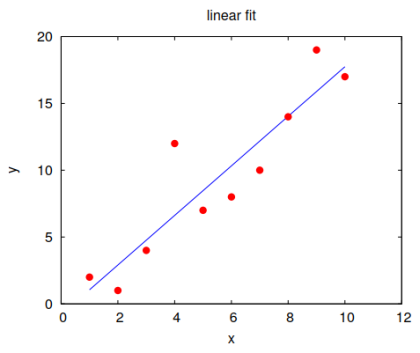
program linearni_regrese !deklarace názvu programu implicit none !tabulka hodnot $[x_i,y_i]$: ![1,2], [2,1], [3,4], [4,12], [5,7], [6,8], [7,10], [8,14], [9,19], [10,17] integer :: i, np !deklarace celočíselných proměnných: !i = pořadové číslo dvojice proměnných, !np = celkový počet diskrétních hodnot parameter (np=10) !zadání fixní hodnoty np double precision, dimension(np) :: x, y !deklarace reálných veličin x, y jako pole
!(vektoru) o np prvcích double precision :: f(np), res(np) !jiný způsob deklarace reálných veličin f, res
!jako pole (vektoru) o np prvcích double precision :: k, q, sumres !deklarace reálných skalárních veličin x=(/(1.d0*i, i=1,np)/) !vektor hodnot regresoru y=(/2.d0, 1.d0, 4.d0, 12.d0, 7.d0, 8.d0, 10.d0, 14.d0, 19.d0, 17.d0/) !vektor hodnot odezvy
!hledané koeficienty lineární funkce: k=(np*SUM(x*y)-SUM(x)*SUM(y))/(np*SUM(x**2.d0)-(SUM(x))**2.d0) q=(SUM(x**2.d0)*SUM(y)-SUM(x)*SUM(x*y))/(np*SUM(x**2.d0)-(SUM(x))**2.d0)
!v záhlaví programu je nutné navíc deklarovat tyto proměnné: integer :: j, INFO, KL, KU, LDAB, LDB, N, RHS parameter(KL=1,KU=1,N=2,KUKL=KL+KU+1,LDAB=2*KL+KU+1,LDB=N,RHS=1) integer :: IPIV(N) double precision :: M(N,N),AB(LDAB,N),B(LDB,RHS) double precision :: max M(1,1)=SUM(x**2.d0) !matice levé strany, M(N,N) M(1,2)=SUM(x) M(2,1)=SUM(x) M(2,2)=np do i=1,N !výpočetní cyklus procedury LAPACK do j=1,N AB(KUKL+i-j, j)=M(i, j) end do end do
B(1,1)=SUM(x*y) !výpočet pravé strany procedurou LAPACK B(2,1)=SUM(y) !volání podprogramu DGBSV: call DGBSV(N,KL,KU,1,AB,LDAB,IPIV,B,N,INFO) if(INFO\bf.ne.0) \bfwrite(*,*) ``INFO='',INFO,``!!!'' k=B(1,1) q=B(2,1)
!společné pokračování: write(1,*) k, q !tisk vypočítaných hodnot do souborufort.1write(1,*) !oddělující řádek do i=1,np !výpočetní cyklus f(i)=k*x(i)+q !výpočet hodnot lineární funkce res(i)=(f(i)-y(i))**2.d0 !výpočet reziduí sumres=SUM(res) !výpočet sumy reziduí end do do i=1,np !zápis cyklu do souboru write(1,*) x(i), y(i), f(i), res(i) end do
write(1,*) write(1,*) sumres !zápis sumy reziduí do souboru
end program linearni_regrese !ukončení programu
C.2.3 Polynomiální regrese metodou nejmenších čtverců
Postup uvedený v předchozím odstavci C.2.2 lze zobecnit pro polynom libovolného ($m$-tého) stupně, kdy analogii rovnice C.10 můžeme přepsat do tvaru (horní indexy zde vždy znamenají mocniny)
kde koeficienty $p_j$ jsou koeficienty $j$-tého stupně polynomu, u lineární regrese tak platí $p_0=q$, $p_1=k$ (viz rovnice C.11). Zároveň je jasné, že počet rovnic $N$ v proceduře LAPACK odpovídá $m+1$. Minimum rovnice C.13 nalezneme, položíme-li $\partial S/\partial p_j=0$, získáme tak soustavu $m+1=N$ lineárních rovnic, které můžeme vyjádřit pomocí maticového zápisu ve tvaru
Výpočetní cyklus procedury LAPACK (viz programový skript v kapitole C.2.2) můžeme takto zobecnit do následující podoby (fortran 95):
do i=1,N-1 !matice levé strany, M(N,N) do j=1,N M(i,j)=SUM(x**(2*N-i-j)) end do end do i=N do j=1,N-1 M(N,j)=SUM(x**(N-j)) end do M(N,N)=np do i=1,N !výpočetní cyklus procedury LAPACK do j=1,N AB(KUKL+i-j, j)=M(i, j) end do end do do i=1,N !výpočet pravé strany procedurou LAPACK B(i,1)=SUM(x**(N-i)*y) end do
V ostatních bodech zůstává programová procedura popsaná v odstavci C.2.2 prakticky nezměněna.
C.2.4 Robustní regrese
V případě, že chceme eliminovat vliv velmi vychýlených (ustřelených
) hodnot, zvolíme
tzv. váženou nebo také robustní regresi. Robustních regresních modelů existuje celá řada (viz například Huber & Ronchetti (2009)),
za všechny zde uvedeme jednoduchou tzv. Tukeyho metodu M-odhadu (Tukey$^\prime$s bisquare method),
založenou na vážení reziduí pomocí dvojí druhé mocniny.
Nejprve spočítáme nevážená rezidua res$\_i=y_i-f(x_i)$ (stejně jako např. v odstavcích C.2.2, C.2.3), potom použijeme následující váhovou funkci:
kde med je medián absolutní odchylky reziduí, kterou můžeme zvolit jako samotné reziduum, nebo odchylku každého rezidua od jejich vlastního mediánu. Váha $w_i=0$, pokud absolutní hodnota rezidua $|\text{res}\_i|>6\,\text{med}$. Extrémně odchýlené hodnoty jsou takto zcela vyřazeny, méně vychýlené hodnoty jsou ponechány, avšak se sníženou váhou.
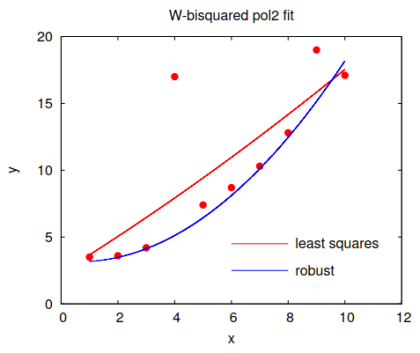
Naprogramování tohoto robustního (váženého) regresního modelu je snadné, do pravé strany rovnice C.14 vložíme vypočítané váhy:
Pro výpočet mediánu existují v každém programovacím jazyce hotové moduly, jako příklad lze použít následující podprogram, výsledek je zahrnut do rovnice C.15 (fortran 95):
subroutine median(i, j, k, np, res, med) implicit none integer :: i, j, k, np double precision :: res(np) double precision, intent(out) :: med double precision :: temp !Seřazení čísel ve vzestupném pořadí: do j=1,np-1 do k=j+1,np if(res(j)$>$res(k))then temp=res(k) res(k)=res(j) res(j)=temp endif end do end do !Výpočet mediánu v případě sudého nebo lichého počtu čísel: if(mod(np,2)==0)then med=(res(np/2)+res(np/2+1))/2.d0 else med=res(np/2+1) endif end subroutine median !Následuje výpočet vah: w(y(i))=(1.d0-(y(i)/6.d0*med)**2.d0)**2.d0, atd.