C.4 Numerické metody výpočtů funkcí více proměnných – řešení parciálních diferenciálních rovnic
C.4.1 Hledání kořenů soustavy funkcí více proměnných – Newtonova-Raphsonova metoda
Newtonova (Newtonova-Raphsonova) metoda představuje velmi účinný nástroj také pro řešení obecné soustavy (nelineárních) rovnic. Soustavu $P$, obsahující $n$ rovnic můžeme obecně zapsat jako
kde $i=1,\,\ldots\,,n$ a kde $\vec{x}$ je vektor proměnných $x_j$. Pomocí Taylorova rozvoje rovnice C.34 do prvního řádu dostáváme obecný výraz pro $k$-tou iteraci ($k$-tý iterativní krok) řešení systému rovnic $P_i$, který můžeme zapsat kompaktní formou
kde vektor $\Delta\vec{x}$ představuje korekci řešení pro každou proměnnou $x_j$ vzhledem k předchozímu iterativnímu kroku. Explicitní zápis vektoru $\Delta\vec{x}\,\,^{k}$ bude mít tvar
Výraz $\vec{P}\,^{k}$ v rovnici C.35 představuje vektor $k$-té iterace všech systémových rovnic ${P\,}^k_i$, zatímco výraz $J\,^{k}$ značí odpovídající Jacobiho matici, jejíž každý prvek ${J\,}^{k}_{ij}$ můžeme snadno analyticky vyjádřit ze systému rovnic ${P\,}^k_i$, položíme-li
Řešíme-li například (jako jednoduchý modelový příklad) soustavu rovnic:
program eqsystem !deklarace názvu programu implicit none !deklarace celočíselných proměnných v záhlaví programu, viz odstavec C.1: integer :: i,j,K,INFO,KL,KU,LDAB,LDB,N,NRHS parameter(N=3,KL=2,KU=2,K=KU+KL+1,LDAB=2*KL+KU+1,LDB=N,NRHS=1) integer :: IPIV(N) !deklarace reálných veličin s dvojitou přesností: double precision :: AB(LDAB,N),B(LDB,NRHS),DER(N,N),C(N),x0,y0,z0 !přesměrování konečného zápisu výsledku do souboru “solve.dat”: open(10,file=“solve.dat”,status=“unknown”) x0=-4.0d0 !odhad vstupní hodnoty xk y0=-3.0d0 !odhad vstupní hodnoty yk z0=14.0d0 !odhad vstupní hodnoty zk do !výpočetní cyklus !matice derivací levých stran DER(1,1)=4.d0*x0**3.d0 DER(1,2)=12.d0*y0 DER(1,3)=-12.d0 DER(2,1)=15.d0*x0**2.d0 DER(2,2)=-3.0 DER(2,3)=2.d0*z0 DER(3,1)=3.d0*x0**2.d0 DER(3,2)=14.d0*y0 DER(3,3)=-1.d0 !transformovaná pásová matice AB podle schematu LAPACK, viz odstavec C.1: do j=1,N do i=max(1,j-KU),min(N,j+KL) AB(K+i-j,j)=DER(i,j) end do end do !matice pravých stran: B(1,1)=-(x0**4.d0+6.d0*y0**2.d0-12.d0*z0-16.d0) B(2,1)=-(5.d0*x0**3.d0-3.d0*y0+z0**2.d0-9.d0) B(3,1)=-(x0**3.d0+7.d0*y0**2.d0-z0) !vlastní výpočet pomocí podprogramu DGBSV, viz odstavec C.1:: call DGBSV(N,KL,KU,1,AB,LDAB,IPIV,B,N,INFO) if (INFO.ne.0) write(*,*) “INFO=”,INFO,“!!!” C=(/(dabs(B(i,1)),i=1,N)/) if (maxval(C).lt.1.d-15) exit !stop kritérium: max|∆x, ∆y, ∆z| < 10−15 x0=B(1,1)+x0 y0=B(2,1)+y0 z0=B(3,1)+z0 !zápis výsledných hodnot x, y, z, ∆x, ∆y, ∆z z jednotlivých iterací do souboru: write(10,*)x0,y0,z0,(B(i,1),i=1,N) end do stop !zastavení celého procesu end program eqsystem !konec programu
| k | xk | yk | zk |
|---|---|---|---|
| 1 | -3.5568659855769229 | -2.8660523504273505 | 14.644631410256411 |
| 2 | -3.4484177335542667 | -2.8088357894123277 | 14.321062859837509 |
| 3 | -3.4422190042021756 | -2.8052747443938260 | 14.300861993036721 |
| 4 | -3.4421993029036972 | -2.8052630869488695 | 14.300795971729505 |
| 5 | -3.4421993027044500 | -2.8052630868291244 | 14.300795971052235 |
| 6 | -3.4421993027044500 | -2.8052630868291244 | 14.300795971052233 |
| k | ∆xk | ∆yk | ∆zk |
|---|---|---|---|
| 1 | 0.44313401442307693 | 0.13394764957264957 | 0.64463141025641035 |
| 2 | 0.10844825202265625 | 5.7216561015022732E-002 | -0.32356855041890148 |
| 3 | 6.1987293520911584E-003 | 3.5610450185016187E-003 | -2.0200866800787826E-002 |
| 4 | 1.9701298478486783E-005 | 1.1657444956463351E-005 | -6.6021307216049201E-005 |
| 5 | 1.9924720437988766E-010 | 1.1974503494876664E-010 | -6.7726957780015056E-010 |
| 6 | 6.2835370146182566E-017 | 1.8208999862070576E-016 | -1.3650720993330078E-015 |
Počáteční odhad (pokud neznáme, jako v případě standardních fyzikálních dějů, nějaké předem očekávané
hodnoty) může být poměrně obtížný – na našem příkladě můžete
vyzkoušet, že pokud zvolíme např. všechny počáteční hodnoty rovny $1$, výpočet zkonverguje rovněž, ovšem bude zapotřebí 24 325 iterací (namísto 6 iterací pro
uvedené blízké celočíselné počáteční odhady).
C.4.2 Principy konečných diferencí
Jednoduchý příklad – jednorozměrná rovnice se dvěma proměnnými: $t$ - čas, $x$ - délka – Burgersova (transportní) parciální diferenciální rovnice
kde $u$ je konstanta (rychlost). Numerický tvar funkce $f(t,x)$ je reprezentován na jednorozměrné síti, tvořené $M$ prostorovými body,
Výpočet proběhne opakovaně během $N$ časových kroků,
Numerické řešení veličiny $f(t,x)$ v obecném $j$-tém prostorovém a $n$-tém časovém ($x=x_j$, $t=t_n$) kroku označíme $f_j^n$. Taylorův rozvoj funkce $f(t,x)$ má tvar
kde $h=\Delta x$ je přírůstek prostorové proměnné $x$ (viz rovnice 1.1) a symbol $\mathcal{O}$ značí zanedbatelný, dále nezapočítávaný příspěvek členů vyšších řádů.
V numerické matematice jsou derivace nahrazeny tzv. diferencemi (viz odstavec C.3.2):
| $ {\dfrac{\partial f}{\partial x}}\bigg|_j^n\approx\left(f_{j+1}^n-f_j^n\right)/\Delta x $ | dopředné diference |
| $ {\dfrac{\partial f}{\partial x}}\bigg|_j^n\approx\left(f_j^n-f_{j-1}^n\right)/\Delta x $ | zpětné diference |
| $ {\dfrac{\partial f}{\partial x}}\bigg|_j^n\approx\left(f_{j+1}^n-f_{j-1}^n\right)/(2\Delta x) $ | centrální diference |
Příklad numerického diferenčního schématu pro aproximace derivací 2. řádu:
Numerické diferenční schéma uvedené transportní (advekční) rovnice C.40 má tvar
kde časový krok je počítán jako dopředná diference a prostorový krok je počítán jako centrální diference. Po jednoduché úpravě dostáváme diferenční rovnici C.48 v programovatelném tvaru:
program explicit !deklarace názvu programu implicit none integer :: j, n, t !deklarace celočíselných proměnných v záhlaví programu: !j = pořadové číslo prostorového kroku, !n = pořadové číslo časového kroku integer :: nj, nn !deklarace celočíselných proměnných v záhlaví programu: !nj = celkový počet prostorových kroků j, !nn = celkový počet časových kroků parameter (nj=100, nn=200) !zadání číselných hodnot pro nj, nn double precision :: x(nj), f(nj), u(nj) !deklarace reálných veličin x, f a u jako pole !(vektoru) o nj prvcích s dvojitou přesností double precision :: dt !deklarace reálné veličiny dt (časového kroku) parameter (dt = 1.d0, u = 1.2d0) !deklarace pevně zadaných hodnot !konstantních reálných veličin do j=1,nj !cyklus počáteční podmínky (počáteční funkce) x(j) = dfloat(j) !příkaz dfloat mění celočíselnou proměnnou na reálnou if (j.le.nj/2) then !tzv. logická podmínka (kde .le. znamená ≤) f(j) = 1.d0 else f(j) = 0.1d0 !zadaná počáteční funkce: pro x ≤ 0.5nj → f = 1.0, !pro x > 0.5nj → f = 0.1 endif end do !konec cyklu t=0.d0 !změna typu proměnné t na real s dvojitou přesností do !vnější (časový) cyklus do j=2,nj-1 !vnitřní (prostorový) cyklus t = t+dt f(j) = f(j)-u(j)*dt*(f(j+1)-f(j-1))/(x(j+1)-x(j-1)) !vlastní rovnice (C.49) end do !konec vnitřního cyklu f(1) = f(1) !vnitřní tzv. pevná okrajová podmínka f(nj) = f(nj-1) !vnější tzv. volná okrajová podmínka do j=1,nj !cyklus zápisu do souboru s názvem fort.100 write (100,*) x(j), f(j) !zápis spočítaných hodnot end do write (100,*) write (100,*) !dvouřádková mezera, nutná pro animaci časových cyklů if (t.gt.200.d0) exit !vystoupení z časového cyklu, pokud t > 200 end do !ukončení časového cyklu stop !zastavení celého procesu při t > 200 end program explicit !konec programu
Toto tzv. explicitní Eulerovo numerické schéma je sice jednoduché, přehledné a názorné, je ale vždy numericky nestabilní (viz obrázek C.4 a odstavec C.4.3.
C.4.3 von Neumannova analýza stability
Jednoduchá analytická metoda, založená na předpokladu periodické numerické poruchy, tedy na Fourierovské dekompozici (rozkladu) numerické chyby. Metoda byla publikována v roce 1947 matematiky Johnem Crankem a Phyllis Nicolsonovou, za spoluautorství významného matematika, fyzika a průkopníka digitálních počítačů Johna von Neumanna.
Předpokládejme obecné poruchy stability (periodické perturbace, vibrace) vlnového charakteru ve tvaru
kde $\xi(k)$ je amplituda vlny, $k$ je vlnové číslo libovolné hodnoty. Pokud $|\xi|>1$, pro $n\rightarrow\infty$ bude
porucha se neustále zvětšuje, numerické schéma je nestabilní. Pokud
numerické schéma je stabilní. Po dosazení poruchové vlnové funkce do explicitního řešení C.49, dostáváme
a po vydělení celé rovnice C.53 výrazem $\xi^ne^{ikj\Delta x}$ dostáváme
Protože $|a+ib|=\sqrt{a^2+b^2}$, bude druhá mocnina rovnice C.54 rovna výrazu
kde pravá strana zjevně bude téměř vždy větší než 1 (výjimečně se bude rovnat 1). Je tedy zřejmé, že v případě explicitního numerického schématu musí vždy platit, že $|\xi|\geq 1$, toto schéma je tedy vždy nestabilní.
C.4.4 Laxova metoda
Numerická varianta explicitního schématu, které podstatně stabilizuje, je pojmenovaná podle matematika Petera Davida Laxe. Základem je jednoduchá změna ve struktuře časového členu. Člen $f_j^n$ v explicitním řešení je zde nahrazen aritmetickým průměrem sousedních hodnot,
von Neumannova analýza stability v tomto případě dává
Schéma je zjevně stabilní, pokud pro tzv. Courant-Friedrichs-Lewyho číslo ${u\Delta t}/{\Delta x}$ (zkráceně Courantovo číslo, cfl) platí
Stejná rovnice C.40, modelovaná Laxovou metodou C.56 je zobrazena v grafu C.5.
C.4.5 Metoda zpětného kroku (Upwind method)
Metoda zpětného kroku používá v prostorovém (advekčním) členu zpětnou diferenci,
von Neumannova analýza stability v tomto případě dává ($\text{cfl}=\alpha$):
Z požadavku $|\xi|^2<1$ vyplývá nerovnost
Protože pokud $\alpha>0$ potom $\cos(k\Delta x)<1$, schéma bude stabilní, pokud obdobně jako v odstavci C.4.4 Courantovo číslo $\alpha<1$.
C.4.6 Laxova-Wendroffova metoda
Dvoukroková metoda, pojmenovaná podle již zmíněného Petera Laxe (viz odstavec C.4.4) a dalšího matematika Burta Wendroffa, kombinuje výhody Laxova a explicitního schématu následujícím způsobem:
1. krok (Laxův) a 2. krok (explicitní):
von Neumannova analýza stability v tomto případě dává ($\text{cfl}=\alpha$):
$\xi=1–2\alpha\sin\left(\frac{k\Delta x}{2}\right)\left[\alpha\sin\left(\frac{k\Delta x}{2}\right)+i\cos\left(\frac{k\Delta x}{2}\right)\right]$, a tedy,
$|\xi|^2=1–4\alpha^2\sin^2\left(\frac{k\Delta x}{2}\right)\left[1-\alpha^2\sin^2\left(\frac{k\Delta x}{2}\right)-\cos^2\left(\frac{k\Delta x}{2}\right)\right].$
Z požadavku $|\xi|^2<1$ opět vyplývá podmínka stability $\alpha<1$.
C.4.7 Implicitní schéma
Princip tzv. implicitního schématu je založen na tom, že hodnoty veličiny $f$ v prostorovém (advekčním) členu na pravé straně rovnice C.49 jsou zadány v čase $t^{n+1}$, tedy de facto v budoucnu, tj. po provedení aktuálního výpočtu,
von Neumannova analýza stability v tomto případě dává (cfl = $\alpha$):
Z rovnice C.66 je tedy zcela zřejmé, že implicitní schéma musí splňovat podmínku stability $|\xi|\leq 1$, je tedy vždy numericky stabilní. Nevýhodou je komplikovanost výpočtu $f_j^{n+1}$ v každém časovém kroku, kdy tuto předem neznámou hodnotu počítáme pomocí tzv. tridiagonální matice (viz odstavce C.1, C.2.1.)
některou z metod nebo knihoven numerické lineární algebry (viz odstavec C.1). Stejná rovnice C.40, modelovaná implicitní metodou C.65-C.67 je zobrazena v grafu C.6.
C.4.8 Příklad pokročilejšího numerického schématu
-
V současnosti existuje celá řada modernějších, přesnějších a stabilnějších numerických metod (viz např. Thompson, 2006):
-
Použití tzv. oddělených sítí (staggered mesh), umožňující oddělení toků různých veličin (flux splitting), například vektorových a skalárních polí, atd.
-
Postupné přidávání jednotlivých členů pravých stran fyzikálních rovnic, reprezentujících různá silová pole (operator splitting):
kde $L_j$ představuje jednotlivé aproximace členů pravé strany rovnice pomocí principu konečných diferencí, $m$ je celkový počet členů na pravé straně rovnice a horní indexy udávají pořadové číslo dílčího časového kroku.$$ \begin{array}{llll}\label{oprourix} (f^1-f^0)/\Delta t & = & L_1(f^0)\\[4pt] (f^2-f^1)/\Delta t & = & L_2(f^1)\\[4pt] \,\,\,\,\,\,\vdots & & \,\,\,\,\,\,\vdots\\[4pt] (f^m-f^{m-1})/\Delta t & = & L_m(f^{m-1}), \end{array} $$C.68 Princip oddělených sítí (staggered mesh): na A-síti
sedí
vektorové veličiny, na B-sítisedí
skalární veličiny (viz obrázek C.7.
Obrázek C.7: Schéma uspořádání tzv. oddělených sítí (staggered mesh). A-síť, určená pro počítání vektorů, je zobrazena černě, B-síť, určená pro počítání skalárních veličin, je zobrazena červeně. Dvojitou čárou je ohraničena vnitřní výpočetní doména ('int'), symbolem 'b' je označena zóna pro počítání okrajových podmínek, symbolem 'g' je označena tzv. ghost zone, což je další přidaná zóna pro okrajové podmínky, nutná pro počítání diferenciálních rovnic 2. řádu nebo v případě symetrických podmínek, například vůči ose sítě (periodické okrajové podmínky), středu sítě, atd. Přesné uspořádání zón pro okrajové podmínky se může v detailech lišit právě podle typu okrajových podmínek (pevné, reflexní, periodické, atd.).
-
Příklad dvoukrokové metody (tj. kdy výpočet následujícího časového kroku je rozdělen na dva mezikroky: explicitně vypočítaný tzv. prediktorový krok, následovaný implicitním tzv. korektorovým krokem) pro výpočet transportní rovnice C.40 skalární veličiny $f$:
$$ \Delta_-^{\text{A}}=\frac{f_{j}^{\text{B}}-f_{j-1}^{\text{B}}}{x^{\text{B}}_{j}-x^{\text{B}}_{j-1}},\quad \Delta_+^{\text{A}}=\frac{f_{j+1}^{\text{B}}-f_{j}^{\text{B}}}{x^{\text{B}}_{j+1}-x^{\text{B}}_{j}}, $$C.69kde $\Delta_-$, $\Delta_+$ jsou symboly pro zpětnou a dopřednou diferenci. Pro výpočet prediktorového kroku použijeme například tzv. van Leerovu derivaci (van Leer, 1982), definovanou jako:
$$ \text{d}_{vL}^{\text{B}}=\left\{ \begin{array}{cl} \langle\Delta_-\Delta_+\rangle=\dfrac{2\Delta_-\Delta_+}{\Delta_-+\Delta_+},&\quad\text{if}\quad\quad\Delta_-\Delta_+>0\\[12pt] \,\,\,\,\,\,\,\,\,\,\,\,0,&\quad\text{if}\quad\quad\Delta_-\Delta_+<0\,. \end{array} \right.\, $$C.70van Leerova derivace je tedy nenulová, pokud je funkce $f$ monotónní a je nulová v těch polích prostorové sítě, kde funkce $f$ prochází extrémy. Důležitou vlastností van Leerovy derivace je, že zachovává monotónnost derivací a zabraňuje vzniku lokálních extrémů: z rovnice C.70 vyplývá, že pokud $\Delta_-\approx\Delta_+\approx\Delta$, potom $\langle\Delta_-\Delta_+\rangle\approx\Delta$ a pokud $\Delta_-\ll\Delta_+$ nebo $\Delta_-\gg\Delta_+$, potom $\langle\Delta_-\Delta_+\rangle\approx{\min}\left(\Delta_-,\Delta_+\right)$. To zaručuje, že hodnoty derivované funkce $f$ na hranicích výpočetní buňky lokálně
nepřestřelí
střední hodnoty funkce $f$ v sousedních buňkách (viz obrázek C.8).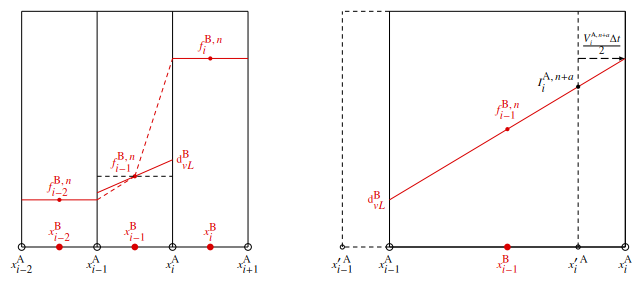
Obrázek C.8: Schématické vyobrazení podmínky monotónnosti van Leerovy derivace (rovnice C.70) je na obrázku C.8a: sklon lineární distribuce veličiny $f$ v prostřední výpočetní buňce (čárkovaná čára) je díky van Leerově derivaci (plná čára označená jako $\text{d}^\text{B}_{vL}$) redukován, takže hodnoty lineárně interpolované, advektované skalární veličiny $f$ na rozhraní buňky musí po celé šířce této buňky „padnout“ mezi hodnoty této veličiny, zprůměrované přes objemy sousedních výpočetních buněk. Obrázek C.8b znázorňuje prediktorový krok advekce skalární veličiny $f$ (rovnice C.71). Veličina je lineárně interpolována (plná červená čára, označená $\text{d}^\text{B}_{vL}$, znázorňuje sklon van Leerovy derivace) a advektována na rozhraní buňky v polovičním časovém kroku $t+\Delta t/2$. Hranice buňky, vyznačené plnou čarou, symbolizují objem látky, advektovaný v čase, zatímco čárkovaná
buňka je pevně fixována v prostoru. Poloha lineárního interpolantu $I$ je označena $I^{\text{A},\,n+a}_j$. Následující korektorový krok (rovnice C.72) advektuje veličinu na střed B-sítě v čase $t+\Delta t$. Výsledkem prediktorového kroku bude veličina $I$ (nazveme ji například interpolant), která je během prediktorového kroku advektována na rozhraní druhé sítě, tj. z původní B-sítě na A-síť a naopak. Prediktorový krok bude mít v tomto případě tvar
$$ I_{j}^{\text{A},\,n+a}=f_{j-1}^{\text{B},\,n}+\text{d}_{vL}^{\text{B}}\left(x^{\text{A}}_{j}-x^{\text{B}}_{j-1}-\frac{u_{j}^{\text{A},\,n+a}\Delta t}{2}\right), $$C.71kde $u$ je advekční rychlost (srovnej rovnici C.49) a horní index $n+a$ označuje dílčí posun v rámci časového kroku $n$.
-
Následující korektorový krok bude dán rovnicí ve tvaru
$$ f_j^{\text{B},\,n+1}=f_j^{\text{B},\,n}-\frac{\Delta t}{x^{\text{A}}_{j+1}-x^{\text{A}}_{j}} \left(I_{j+1}^{\,\text{A},\,n+a}u^{\text{A},\,n+a}_{j+1}-I_{j}^{\,\text{A},\,n+a}u^{\text{A},\,n+a}_{j}\right). $$C.72Po provedení korektorového kroku se tedy skalární veličina $f$ opět vrací na B-síť, tj. uprostřed mezi polohy $\text{A}(j+1),\,\text{A}(j)$. Rovnice C.72 je zároveň numerickou formou jednorozměrné divergence. Obdobné schéma ve dvoj a trojrozměrné verzi se nazývá metoda konečných objemů (finite volume method - viz např. LeVeque (2002)). Vícerozměrná podoba rovnice C.72 (počítaná v souřadnicovém směru $j$, index $k$ zde symbolizuje všechny ostatní souřadnicové směry, v závislosti na dimenzi výpočetní sítě) by tedy vypadala:
$$ f_{j,k}^{\text{B},\,n+1}=f_{j,k}^{\text{B},\,n}-\frac{\Delta t}{V^{\text{B}}_{j,k}} \left(I_{j+1,k}^{\,\text{A},\,n+a}u^{\text{A},\,n+a}_{j+1,k}S^{\text{A}}_{j+1,k}- I_{j,k}^{\,\text{A},\,n+a}u^{\text{A},\,n+a}_{j,k}S^{\text{A}}_{j,k}\right), $$C.73kde veličina $V^\text{B}_{j,k}$ znamená objem jedné tzv. buňky výpočetní sítě (grid cell), středovaný na síti B, veličina $S^\text{A}_{j,k}$ znamená potom plochu této buňky (nacházející se na síti A), přes niž prochází tok veličiny $f$ ve směru $j$ (viz odstavce A.1.2, A.2.2, A.3.2, A.7.2, popisující vztahy mezi těmito veličinami v různých souřadnicových soustavách – viz také obrázek C.8). Pokud bychom modelovali transportní rovnici C.40 pro vektorovou veličinu, bude postup zcela obdobný, pouze namísto ze sítě B budeme vycházet ze sítě A, prediktorový krok transportuje tuto veličinu na síť B a následný korektorový krok opět na síť A.
-
Stejná rovnice C.49, modelovaná uvedenou metodou prediktor-korektor je uvedená na obrázku C.9. Courantovo číslo $\text{cfl}=0.5$.
Obrázek C.9: Animace postupné hustotní vlny, popsané Burgersovou rovnicí C.40, modelované metodou prediktor-korektor (pomocí rovnic C.71 a C.72). Křivka hustoty je na rozdíl od předchozích schématů stabilní a ostrá, malý sklon čela vlny je dán hustotou výpočetní sítě (vzdáleností sousedních prostorových bodů). Tvar vlny lze korigovat přidáním střihové tzv. Navier-Stokesovy viskozity nebo objemové, tj. v praktických výpočtech používané tzv. numerické viskozity (viz například LeVeque, 2002 a další). Numerické schéma, uvedené v tomto odstavci, není zdaleka jediné možné, představuje pouze ukázku tzv. po částech lineární metody (Piecewise Linear Method), kdy numerické diference jsou prokládány úsečkami. Je možné použít i přesnější tzv. po částech parabolickou metodu (Piecewise Parabolic Method – PPM, viz např. Colella & Woodward (1984)), nevýhodou je ovšem zcela zákonitě vyšší výpočetní náročnost, tj. nároky na výkon počítačů, atd. Kromě toho existuje celá řada jiných metod, založená na jiných principech numerického derivování, jiných typech prostorových sítí (například tzv. adaptivní sítě, které se v průběhu času samy mění), nebo k výpočtům vůbec prostorové sítě nevyužívají – např. tzv. SPH metoda (Smooth Particle Hydrodynamics), atd.
C.4.9 Příklady modelování reálných fyzikálních procesů
Riemannova-Sodova rázová trubice
Základní testovací úloha pro většinu numerických kódů se snadno ověřitelnými výsledky. Jedná se o uzavřenou trubici, respektive box, rozdělený na dvě části pevnou přepážkou, nazývanou též diafragma (latinský název pro bránici), kde obě oddělení jsou naplněné plynem s rozdílnými hustotami a tlaky. Náhle přepážka zmizí což vyvolá pohyb plynu předcházený rázovou vlnou šířící se kolmo k rovině původní přepážky ve směru řidšího plynu.
Obrázek C.10a ukazuje snímek průběhu hustoty, kdy počáteční stav plynu (kde index $L$ označuje levou stranu trubice s vyšší počáteční hustotou a tlakem , index $R$ označuje pravou stranu trubice s nižší počáteční hustotou a tlakem) je zvolen následovně: $\rho_L=1.0$, $\rho_R=0.125$, $P_L=1.0$, $P_R=0.1$, $\gamma=5/3$ kde $\rho$ je hustota, $P$ je tlak a $\gamma$ je adiabatická konstanta.
Obrázek C.11a ukazuje obdobnou testovací úlohu s počátečními průběhy veličin proměnnými v obou směrech $x,\,y$, s následujícími parametry:
$\rho_L=\text{e}^{-y^2}$, $\rho_R=0.125\,\text{e}^{-y^2}$, $P_L=\text{e}^{-y^2}$, $P_R=0.1\,\text{e}^{-y^2}$,
$\gamma=5/3$. Profily hustoty a tlaku v příčném směru $y$ jsou tedy Gaussovské
.
V tomto modelu je ještě přidána porucha
, způsobená malou počáteční složkou rychlosti $V_y=0.05$.
poruchazpůsobí určitou příčnou deformaci toku, kde jsou rovněž viditelné Kelvinovy-Helmholtzovy a Rayleigh-Taylorovy nestability.
Kelvinova-Helmholtzova nestabilita
Dalším oblíbeným testovacím problémem je modelování Kelvinovy-Helmholtzovy nestability (viz např. Chandrasekhar, 1961, viz také obrázek C.12). Pravoúhlá oblast (box) je naplněná plynem se dvěma opačně směřujícími toky, oddělenými lineární pomyslnou diskontinuitou.
Okrajové podmínky jsou periodické na čelních okrajích toků, tj. v obrázku C.12b na stranách se souřadnicemi $x=0$ a $x=1$,
zatímco na zbývajících dvou stranách jsou zvoleny opět jako pevné stěny
.
Počáteční podmínky k úloze jsou převzaty z parametrů, uvedených v instrukcích ke kódu ATHENA (Stone et al., 2008
; Springel, 2013):
pro $y>0.5$ je podélná rychlost toku $V_{x,1}=0.3$ a hustota plynu $\rho_1=1$, pro $y\leq 0.5$ je podélná rychlost toku $V_{x,2}=-0.3$ a hustota plynu $\rho_2=2$.
Počáteční tlak $P=1.0$ v celé výpočetní oblasti a adiabatický exponent $\gamma=5/3$.
Abychom se vyhnuli naprosto ostrému rozhraní mezi oběma toky, definujeme přechodovou oblast která propojí oba toky, popsanou rovnicemi (Springel, 2013):
která charakterizuje počáteční poruchu hustoty ve směru $y$, podobně
která charakterizuje počáteční poruchu $x$-ové složky rychlostního pole ve směru $y$, kde střední kvadratická odchylka rychlosti $\sigma=0.01$. Do těchto počátečních podmínek vložíme periodickou poruchu $y$-ové složky rychlosti ve tvaru
s vlnovým číslem $k=2\times(2\pi/L)$ a amplitudou poruchy $A=0.05$.
Význam tohoto testu spočívá také ve snadném ověření linearity nárůstu poruchy v rané fázi průběhu úlohy, zatímco později je průběh vývoje poruchy zjevně nelineární,
což vylučuje provedení analytických kvantitativních výpočtů. Navíc, ostrost
rozhraní mezi oběma protisměrnými toky může sloužit jako
indikátor tzv. numerické difúzivity (tj. stabilizace algoritmu advekčního schématu pomocí druhých derivací toku) výpočetního schématu (Stone et al., 2008).