4 Křivkový integrálVe výsledcích příkladů s geometrickými nebo fyzikálními veličinami nejsou uváděny příslušné jednotky.

4.1 Křivkový integrál 1. druhu

Křivkovým integrálem 1. druhu nazýváme integrál $\displaystyle\int_{\mathcal{C}}f\,\text{d} s$ obecné skalární funkce $f(x,y,z)$ podél křivky $\mathcal{C}$, kde $\text{d} s$ je délkový element křivky: $\text{d} s^2=\text{d} x^2+\text{d} y^2+\text{d} z^2$ (Pythagorova věta v diferenciálním tvaru). Stanovíme-li např. souřadnici $x$ jako nezávisle proměnnou a $y(x)$, $z(x)$ jako závisle proměnné, můžeme psát

$$ \int_{\mathcal{C}}f\,\text{d} s=\int_{x_1}^{x_2}f(x,y,z)\sqrt{1+\left(\frac{\text{d} y}{\text{d} x}\right)^2+\left(\frac{\text{d} z}{\text{d} x}\right)^2}\,\text{d} x. $$

4.1

Nalezneme-li vhodný parametr $t$, potom bude parametrizovaná rovnice 4.1, kde $f(t)=f\left[x(t),y(t),z(t)\right]$, $s(t)=s\left[x(t),y(t),z(t)\right]$, mít tvar

$$ \int_{\mathcal{C}}f(t)\frac{\text{d} s(t)}{\text{d} t}\,\text{d} t=\int_{t_1}^{t_2}f(t)\sqrt{\left(\frac{\text{d} x}{\text{d} t}\right)^2+\left(\frac{\text{d} y}{\text{d} t}\right)^2+ \left(\frac{\text{d} z}{\text{d} t}\right)^2}\,\text{d} t. $$

4.2

Pomocí křivkového integrálu 1. druhu lze určit geometrické a fyzikální charakteristiky dané křivky. Položíme-li $f=1$, výsledkem bude délka křivky $\mathcal{C}$. Položíme-li $f=\tau$ (délková hustota křivky), dostáváme $\tau\,\text{d} s=\text{d} m$, tedy element hmotnosti křivky, výsledkem integrace bude hmotnost křivky $\mathcal{C}$,

$$ m=\int_\mathcal{C}\,\text{d} m=\int_{\mathcal{C}}\tau\,\text{d} s. $$

4.3

Pokud položíme například $f=z\tau$, dostáváme tzv. statický moment $S_z$ křivky vzhledem k ose $z$, jeho vydělením hmotností dostáváme $z$-ovou souřadnici středu hmotnosti $z_T$ křivky $\mathcal{C}$ (obdobně pro ostatní souřadnicové směry), tedy

$$ x_T=\frac{1}{m}\int_{\mathcal{C}}x\,\text{d} m=\frac{1}{m}\int_{\mathcal{C}}x\tau\,\text{d} s,\quad y_T=\frac{1}{m}\int_{\mathcal{C}}y\,\text{d} m,\quad z_T=\frac{1}{m}\int_{\mathcal{C}}z\,\text{d} m. $$

4.4

Položíme-li $f=r^2\tau$, kde $r$ je vzdálenost obecného bodu křivky od zvolené přímky v prostoru (osy $o$), dostáváme moment setrvačnosti $J_o$ křivky $\mathcal{C}$ vzhledem k této ose. Momenty setrvačnosti křivky $\mathcal{C}$ např. vzhledem k jednotlivým kartézským souřadnicovým osám potom budou

$$ \begin{aligned} J_x&=\int_{\mathcal{C}}(y^2+z^2)\,\text{d} m=\int_{\mathcal{C}}(y^2+z^2)\,\tau\,\text{d} s,\\ J_y&=\int_{\mathcal{C}}(z^2+x^2)\,\text{d} m,\\ J_z&=\int_{\mathcal{C}}(x^2+y^2)\,\text{d} m. \end{aligned} $$

4.5

nahoru

Příklady

4.1

Vypočítejte délku křivky $s=\displaystyle\int_\mathcal{C}\left(x^2+y^2\right)\,\text{d} s$, kde $\mathcal{C}$ je křivka s parametrizací $x=a(\cos t+t\sin t)$, $y=a(\sin t-t\cos t)$, $t\in\langle 0,2\pi\rangle$.

$s=a^3\left(2\pi^2+4\pi^4\right)$

4.2

Vypočítejte délku úseku paraboly $y=x^2$, ohraničeného body $(-2,4)$ a $(2,4)$.

$s=2\sqrt{17}+\ln\sqrt{4+\sqrt{17}}\approx 9,2936$

4.3

Kolikrát delší bude skutečná trajektorie $s$ šikmého vrhu (s počátečním a koncovým bodem ve stejné výšce)

s maximálním možným doletem $D$,
$s=\left[\dfrac{1}{\sqrt{2}}+\ln\sqrt{1+\sqrt{2}}\right]D\approx 1,\!15 D$
pokud počáteční (elevační) úhel $\alpha=30^\circ$,
$s=\left[\dfrac{1}{\sqrt{3}}+\dfrac{\sqrt{3}\ln\sqrt{3}}{2}\right]D\approx 1,\!05 D$
pokud elevační úhel $\alpha=60^\circ$,
$s=\left[1+\dfrac{\ln\sqrt{2+\sqrt{3}}}{\sqrt{3}}\right]D\approx 1,\!38 D$
pokud elevační úhel bude takový aby maximální výška trajektorie se rovnala doletu,
$s=\left[\dfrac{\sqrt{17}}{2}+\dfrac{\ln\sqrt{4+\sqrt{17}}}{4}\right]D\approx 2,\!32 D$

než příslušný dolet?

Dokažte, že pro $\alpha=\dfrac{\pi}{2}$, $\dfrac{s}{D}\rightarrow\infty$, a rovněž že pro $\alpha=0$, $\dfrac{s}{D}\rightarrow 1$.

$s=\dfrac{1}{2}\left[\dfrac{1}{\cos\alpha}+\ln\left(\dfrac{1+\sin\alpha}{\cos\alpha}\right)\,\text{cotg}\,\alpha\right]D$

4.4

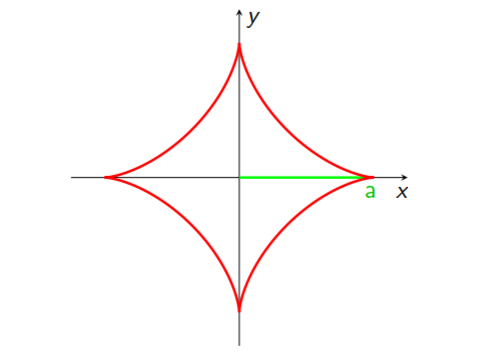
Přímým výpočtem v kartézských souřadnicích a také pomocí vhodné parametrizace vypočítejte hmotnost asteroidy $x^{2/3}+y^{2/3}=a^{2/3}$ s délkovou hustotou $\tau=x^{4/3}+y^{4/3}$ (viz obrázek 4.1). Parametrizace asteroidy může být například: $x=a\cos^3t,\,y=a\sin^3t$, kde $t$ neznačí čas, nýbrž úhlový parametr.

Obrázek 4.1: Asteroida. Délka poloosy a je vyznačena zelenou barvou.

Animace vzniku rotačního tělesa, odvozeného z asteroidy.

Statický obrázek — Obrázek 4.1: Asteroida. Délka poloosy a je vyznačena zelenou barvou.

Animace vzniku rotačního tělesa, odvozeného z asteroidy.

$m=4a^{7/3}$

4.5

Pomocí parametrizace $x=a\cos t,\,y=a\sin t,\,z=bt$, vypočítejte hmotnost jednoho závitu válcové šroubovice s délkovou hustotou $\tau=\dfrac{z^2}{x^2+y^2}$.

$m=\dfrac{8\pi^3}{3}\left(\dfrac{b}{a}\right)^2\sqrt{a^2+b^2}$

4.6

Pomocí vhodné parametrizace a s použitím obecných koeficientů vypočítejte hmotnost jednoho závitu válcové šroubovice s délkovou hustotou $\tau=\dfrac{1}{x^2+y^2+z^2}$.

$m=\dfrac{\sqrt{a^2+b^2}}{ab}\text{arctg}\,\dfrac{2\pi b}{a}$

4.7

Pomocí parametrizace $x=at\cos t,\,y=at\sin t,\,z=bt$, vypočítejte hmotnost jednoho závitu kuželové šroubovice s délkovou hustotou $\tau=2\sqrt{x^2+y^2}-z$.

$m=\dfrac{2a-b}{3a^2}\left[\sqrt{\left(a^2+b^2+4\pi^2a^2\right)^3}-\sqrt{\left(a^2+b^2\right)^3}\right]$

4.8

Dokažte vztah $s=\displaystyle\int_{\phi_1}^{\phi_2}\sqrt{f^2+\dot{f}^2}\,\text{d} \phi$, kde $s$ je délka hladké křivky, vyjádřené v polárních souřadnicích $r=f(\phi)$, a kde $\dot{f}=\text{d} f/\text{d}\phi$.

z transformačních vztahů pro polární souřadnice a z definice křivkového integrálu

4.9

Dokažte vztah $s=\displaystyle\int_{\theta_1}^{\theta_2}\sqrt{f^2+\dot{g}^2\left(f^2\sin^2\theta+\dot{f}^2\right)}\,\text{d} \theta$, kde $s$ je délka hladké křivky, vyjádřené v kulových souřadnicích $r=f(\phi)$, $\phi=g(\theta)$, a kde $\dot{f}=\text{d} f/\text{d}\phi$, $\dot{g}=\text{d} g/\text{d}\theta$.

z transformačních vztahů pro kulové souřadnice a z definice křivkového integrálu

4.10

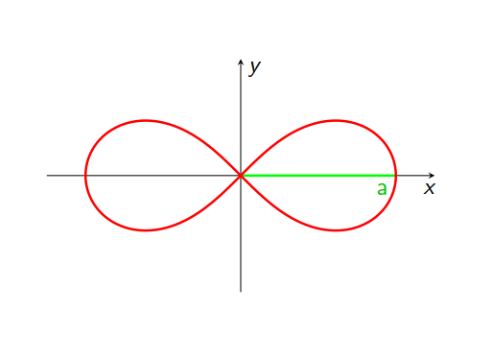
Pomocí vhodné transformace souřadnic vypočítejte hmotnost Bernoulliovy lemniskáty (obrázek 4.2) s kartézskou rovnicí $(x^2+y^2)^2=a^2(x^2−y^2)$, s délkovou hustotou $\tau=|y|$. Vyjděte z principu uvedeného v příkladu 4.8 nebo použijte transformační rovnice: $x=a\cos t/(1+\sin^2t),\,y=a\sin t\cos t/(1+\sin^2t)$, kde $t=\arcsin(\text{tg}\,\phi)$ je úhlový parametr (rozvažte vždy správné integrační meze pro zvolený parametr v rámci příslušného kvadrantu).

Obrázek 4.2: Bernoulliova lemniskáta. Délka poloosy a je vyznačena zelenou barvou.
Animace vzniku rotačního tělesa, odvozeného z Bernoulliovy lemniskáty.

$m={2a^2}\left(2-\sqrt{2}\right)$

4.11

Přímým výpočtem v kartézských souřadnicích a také pomocí vhodné transformace souřadnic vypočítejte hmotnost nehomogenní křivky s délkovou hustotou $\tau=x+y$, která vznikne průnikem ploch $x^2+y^2+z^2=a^2$, $x=y$, v 1. oktantu.

$m=\sqrt{2}a^2$

4.12

Vypočítejte hmotnost oblouku elipsy $\dfrac{x^2}{9}+\dfrac{y^2}{4}=1$ v 1. kvadrantu. Délková hustota $\tau=xy$.

$m=\dfrac{38}{5}$

4.13

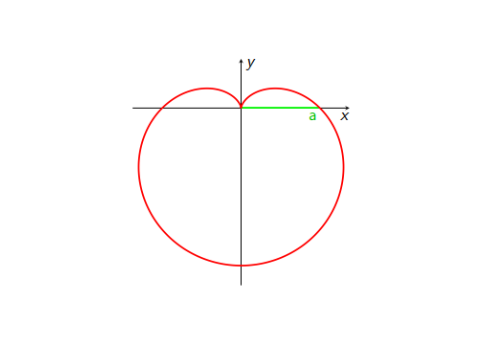
Vypočítejte celkovou délku $s$ a hmotnost $m$ kardioidy (obrázek 4.3) s polární rovnicí $r=a\left(1−\sin\phi\right)$, s délkovou hustotou $\tau=|x|$.

Obrázek 4.3: Kardioida. Délka konstanty a je vyznačena zelenou barvou.
Animace vzniku rotačního tělesa, odvozeného z kardioidy.

$s=8a,\quad m=\dfrac{32\,a^2}{5}$

4.14

Určete souřadnice těžiště $T$ půlkružnice (procházející 1. a 2. kvadrantem) a čtvrtkružnice (procházející 1. kvadrantem), obojí s délkovou hustotou $\tau=y$.

$T=\left[0,\dfrac{\pi a}{4}\right]$, $T=\left[\dfrac{a}{2},\dfrac{\pi a}{4}\right]$

Určete jejich momenty setrvačnosti, pokud se budou otáčet okolo svých geometrických os.

$J=2a^4$, $J=a^4$

4.15

Určete souřadnice těžiště $T$ jednoho oblouku cykloidy $x = a(t-\sin t)$, $y = a(1-\cos t)$, $t\in\langle 0,2\pi\rangle$, s homogenní délkovou hustotou $\tau(x,y)=1$.

$T=\left[\pi a,\dfrac{4a}{3}\right]$

4.16

Drát má tvar kružnice $x^2+y^2=a^2$. Vypočítejte jeho moment setrvačnosti $J$, pokud se drát otáčí okolo svého průměru. Jeho délková hustota $\tau=|x|+|y|$.

$J=4a^4$

4.17

Vypočítejte délku $\ell$ dvou závitů (viz obrázek 4.4) a moment setrvačnosti $J$ následujících křivek s konstantní délkovou hustotou $\tau$, rotujících okolo osy $z$ (procházející počátkem, kolmo k vyobrazené rovině):

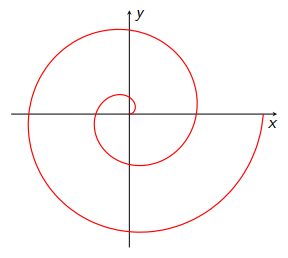
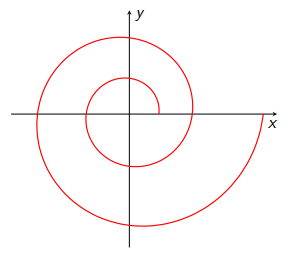
Archimedova spirála — Obrázek 4.4: Dva závity spirály s polárním úhlem $\phi\in\langle 0,4\pi\rangle$. Vlevo: Archimédova spirála, vpravo: logaritmická spirála.

Obrázek 4.4: Dva závity spirály s polárním úhlem $\phi\in\langle 0,4\pi\rangle$. Vlevo: Archimédova spirála, vpravo: logaritmická spirála.

Archimédovy spirály, dané v polárních souřadnicích předpisem $r=\alpha\phi$, kde $\alpha$ je kladná konstanta a polární úhel $\phi\in\langle 0,4\pi\rangle$
$l = \dfrac{\tau\alpha^3}{8}\left[4\pi\left(32\pi^2+1\right)\sqrt{16\pi^2+1}-\ln\left(4\pi+\sqrt{16\pi^2+1}\right)\right]\approx 0,492\,mR^2$
logaritmické spirály, dané v polárních souřadnicích předpisem $r=\alpha\,\text{e}^{\beta\phi}$, kde $\alpha$ a $\beta$ jsou kladné konstanty a kde polární úhel $\phi\in\langle 0,4\pi\rangle$.
$\ell=\dfrac{\alpha}{\beta}\sqrt{\beta^2+1}\left(\text{e}^{4\pi\beta}-1\right)$, $J=\dfrac{\tau\alpha^3}{3\beta}\sqrt{\beta^2+1}\left(\text{e}^{12\pi\beta}-1\right)=\left(1+\text{e}^{-4\pi\beta}+\text{e}^{-8\pi\beta}\right)\dfrac{mR^2}{3}$
jak se změní úloha (b), pokud počátek spirály bude v bodě $[0,0]$?
$\ell=\dfrac{\alpha}{\beta}\sqrt{\beta^2+1}\,\,\text{e}^{4\pi\beta}$

Výsledek také vyjádřete jako funkci hmotnosti křivky $m=\tau\ell$ a největší vzdálenosti křivky od osy rotace $R=r_\text{max}$.

$J=\dfrac{\tau\alpha^3}{3\beta}\sqrt{\beta^2+1}\,\,\text{e}^{12\pi\beta}=\dfrac{mR^2}{3}$