7.3 Gaussova (Gaussova-Ostrogradského) větaPokud není uvedeno jinak, myslí se vždy tok ve směru vnější normály uvedené uzavřené plochy.
Gaussova věta, nazývaná také Gaussův teorém nebo teorém divergence, říká, že tok vektorového pole uzavřenou plochou $S$ se rovná integrálu divergence tohoto pole přes objem $V$, ohraničený touto plochou (větu lze zobecnit pro $n$-rozměrný Eukleidovský prostor). Matematický zápis Gaussovy věty má tvar
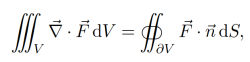
7.3
kde $\vec{F}$ je obecné vektorové pole, $\vec{n}$ je jednotkový vektor vnější normály plochy $S$, $\partial{V}$ značí hraniční oblast objemu $V$ (plochu $S$).
Příklady
7.31
Pomocí Gaussovy věty odvoďte vztah pro výpočet objemu válce o poloměru $R$ a výšce $H$.
Pomocí identity $V=\displaystyle\int_V\text{div}\,\vec{F}\,\text{d} V\,(\text{div}\,\vec{F}=1)= \displaystyle\iint_{\partial V}\vec{F}\cdot\vec{n}\,\text{d} S$, $V=\pi R^2H$
7.32
Pomocí Gaussovy věty odvoďte vztah pro výpočet objemu koule o poloměru $R$.
Stejným způsobem jako v předešlém příkladě, $V=\dfrac{4}{3}\pi R^3$
7.33
Pomocí Gaussovy věty odvoďte vztah pro výpočet objemu kužele o poloměru $R$ a výšce $H$.
$V=\dfrac{\pi R^2H}{3}$
7.34
Pomocí Gaussovy věty odvoďte vztah pro výpočet objemu anuloidu (toroidu) o poloměru osy toru $R$ a poloměru trubice $a$.
$V=2\pi^2Ra^2$
7.35
Pomocí Gaussovy věty odvoďte vztah pro výpočet objemu osově symetrického tělesa $\mathcal{M}$ s osou $(0,0,z)$: $\mathcal{M}=\{(x,y,z)\,|\,\sqrt{x^2+y^2}\le a\sin\theta,\,z\le a\sin\theta\cos\theta,\,\theta\in\langle 0,\pi\rangle\}$.
Povrch tělesa je vytvořen rotací rovinné křivky, tzv. Geronovy (Huygensovy) lemniskáty, okolo osy ležící v rovině křivky a procházející jejím středem -
viz obrázek 7.1 (kde osa $y$ bude nyní osou $z$), viz také příklad 7.6.
$V=\dfrac{\pi^2 a^3}{4}$
7.37
Pomocí Gaussovy věty odvoďte vztah pro výpočet objemu osově symetrického tělesa $\mathcal{M}$ vytvořeného rotací uzavřené smyčky Descartova listu z příkladu 7.8 okolo osy $y$, vyznačené v obrázku 7.2.
$V=\dfrac{4\pi^2 a^3}{3\sqrt{3}}$
Určete rovněž maximální délku $L$ smyčky, tj. délku podél přímky, půlící 1. kvadrant v uvedeném obrázku
a souřadnice horizontálního i vertikálního maxima, vše jako funkci konstanty $a$.
$L=\dfrac{3}{\sqrt{2}}a,\,(2^{\frac{2}{3}}a,2^{\frac{1}{3}}a),\,(2^{\frac{1}{3}}a,2^{\frac{2}{3}}a)$
7.38
Pomocí Gaussovy věty určete polohu středu hmotnosti homogenního tělesa z příkladu 7.37 ve směru svislé osy, vyznačené v obrázku 7.2.
$z_T=\dfrac{27\sqrt{3}}{16\pi}a$
7.39
Pomocí Gaussovy věty odvoďte moment setrvačnosti homogenního tělesa $\mathcal{M}$ z příkladu 7.35, rotujícího okolo osy $(0,0,z)$. Výsledek vyjádřete v jednotkách hmotnosti tělesa $M$ a poloměru $a$.
$J=\dfrac{M a^2}{2}$
7.40
Pomocí Gaussovy věty odvoďte moment setrvačnosti homogenního tělesa $\mathcal{A}$ z příkladu 6.50, rotujícího okolo stejné osy $y$. Výsledek vyjádřete v jednotkách hmotnosti tělesa $M$ a poloosy $a$.
$J=\dfrac{96}{143}M a^2$
7.41
Pomocí Gaussovy věty určete moment setrvačnosti homogenního tělesa z příkladu 7.37, rotujícího okolo svislé osy, vyznačené v obrázku 7.2. Výsledek vyjádřete v jednotkách hmotnosti tělesa $M$ a maximálního rozměru $R$ smyčky v horizontálním směru.
$J=\dfrac{81\sqrt{3}}{40\pi}\dfrac{MR^2}{2^{{4}/{3}}}$
7.42
Pomocí Gaussovy věty určete tok vektorového pole $\vec{F}=\left(x^2,y^2,z^2\right)$ uzavřenou plochou, určenou předpisem $S=\left\{(x,y,z)\,|\,x\in\langle A,\,2A\rangle,\,y\in\langle B,\,2B\rangle,\,z\in\langle C,\,2C\rangle\right\}$.
$\Phi_F=3ABC(A+B+C)$
7.43
Pomocí Gaussovy věty určete tok vektorového pole $\vec{F}=\left(x^2,y^2,z^2\right)$ uzavřenou plochou, určenou předpisem $S=\left\{(x,y,z)\,|\,x^2+y^2=R^2,\,z\in\langle 0,\,H\rangle\right\}$.
$\Phi_F=\pi R^2H^2$
7.44
Pomocí Gaussovy věty určete tok vektorového pole $\vec{F}=\left[(x-1)^2,(y-1)^2,z^2\right]$ povrchem tělesa, určeného předpisem $\mathcal{V}=\left\{(x,y,z)\,|\,x^2+y^2\leq R^2,\,y\geq 0,\,z\in\langle 0,H\rangle\right\}$.
$\dfrac{4}{3}R^3H+\dfrac{\pi R^2H^2}{2}-2\pi R^2H$
7.45
Pomocí Gaussovy věty určete tok vektorového pole $\vec{F}=\left(x^2,y^2,z^2\right)$ uzavřenou plochou, tvořenou povrchem tělesa z příkladu 6.45.
$\Phi_F=\dfrac{\pi R^2H^2}{3}$
7.46
Pomocí Gaussovy věty určete tok vektorového pole $\vec{F}=\left(x^3-y^3,x^3+y^3,z\right)$ uzavřenou plochou, tvořenou povrchem tělesa $\mathcal{V}=\left\{(x,y,z)\,|\,z\in\langle 0,\,H\rangle,\,x^2+y^2\le\dfrac{R^2}{H^2}(H-z)^2\right\}$.
$\Phi_F=\dfrac{\pi R^2H}{30}\left(9R^2+10\right)$
7.47
Pomocí Gaussovy věty určete tok vektorového pole $\vec{F}=(x^3,y^3,z^3)$ plochou, určenou předpisem $S=\left\{(x,y,z)\,|\,x^2+y^2+z^2=R^2\right\}$.
$\Phi_F=\dfrac{12}{5}\pi R^5$
7.48
Je dáno silové pole $\vec{F}=(x^3-x^2,\,y^3-y^2,\,z^3-z^2)$. Pomocí Gaussovy věty určete jeho tok povrchem tělesa, určeného předpisem $\mathcal{V}=\left\{(x,y,z)\,|\,x,y,z\in\langle 0,R\rangle,\,x^2+y^2+z^2\le R^2\right\}$.
$\Phi_F=\dfrac{3\pi R^4}{40}\left(4R-5\right)$
7.49
Pomocí Gaussovy věty vypočítejte tok vektorového pole $\vec{F}=(x,y,z)$ uzavřenou plochou, tvořenou povrchem tělesa z příkladu 7.35. Proč je výsledná hodnota trojnásobkem výsledné hodnoty z uvedeného příkladu?
$\Phi_F=\dfrac{3\pi^2 a^3}{4}$
7.50
Pomocí Gaussovy věty vypočítejte tok vektorového pole $\vec{F}=(x^3,y^3,z^3)$ uzavřenou plochou, tvořenou povrchem tělesa z příkladu 7.35.
$\Phi_F=\dfrac{27}{64}\pi^2 a^5=\left(\dfrac{3}{4}\right)^3\pi^2 a^5$
7.51
Pomocí Gaussovy věty vypočítejte tok $\Phi$ vektorového pole $\vec{F}(x,y,z)=(0,0,z^2)$ uzavřenou plochou, tvořící povrch tělesa: $\mathcal{V}=\big\{(x,y,z)\,\big|\,x^2+y^2\le 4$, $x\leq 0$, $y\geq 0$, $z\in\langle 0,|x|\rangle\big\}.$
$\Phi_F=\pi$
7.52
Pomocí Gaussovy věty vypočítejte tok $\Phi$ vektorového pole $\vec{F}(x,y,z)=(0,0,z^2)$ uzavřenou plochou, tvořící povrch tělesa: $\mathcal{V}=\big\{(x,y,z)\,\big|\,x^2+y^2+z^2\leq 4$, $x\geq 0$, $y\leq 0$, $z\geq 0$, $\dfrac{z^2}{x^2+y^2+z^2}\leq\dfrac{1}{2}\big\}.$
$\Phi_F=\pi$
7.53
Pomocí plošného integrálu 2. druhu i pomocí Gaussovy věty vypočítejte tok $\Phi$ vektorového pole $\vec{F}(x,y,z)=(0,0,z^2)$ uzavřenou plochou, tvořící povrch tělesa: $\mathcal{V}=\big\{(x,y,z)\,\big|\,x^2+y^2+z\leq 9\wedge z-3x^2–3y^2\geq 0\big\}.$
$\Phi_F=21\pi\left(\dfrac{9}{4}\right)^2$
7.54
Pomocí plošného integrálu 2. druhu i pomocí Gaussovy věty vypočítejte tok $\Phi$ vektorového pole $\vec{F}(x,y,z)=(x^2,0,0)$ uzavřenou plochou, tvořící povrch tělesa: $\mathcal{V}=\big\{(x,y,z)\,\big|\,x^2+y^2+z\leq 5$, $x\geq 0$, $y\leq 0$, $z\ge 1\big\}.$
$\Phi_F=\dfrac{56}{5}$
7.55
Určete kapacitu válcového kondenzátoru, který tvoří dvě souosé vodivé válcové slupky (elektrody) s poloměry $R_1$ a $R_2$ a délkou $H$, kde $R_1<R_2$. Na vnitřní elektrodu je přiveden náboj $+Q$, na vnější elektrodu náboj $-Q$. Zanedbejte nepravidelnosti elektrického pole na obou koncích elektrod.
$C=\dfrac{2\pi\epsilon_0H}{\ln(R_2/R_1)}$
7.56
Určete kapacitu kulového kondenzátoru, který tvoří dvě soustředné vodivé kulové slupky (elektrody) s poloměry $R_1$ a $R_2$, kde $R_1<R_2$. Na vnitřní elektrodu je přiveden náboj $+Q$, na vnější elektrodu náboj $-Q$.
$C={4\pi\epsilon_0}\dfrac{R_1R_2}{R_2-R_1}$