Half-plane intersection

Introduction

In this chapter, we will show you how to describe and find the intersection of $n$ half-planes in the plane effectively. We want to proceed recurrently according to the "divide and conquer" strategy. That is, we divide the set

of given half-planes into two parts $H_1$ and $H_2$ of roughly same size and we compute the intersection

as an intersection $C_1 \cap C_2$, where

A major role for the gradual computing of intersections $C_1\cap C_2$ has the way how we describe these intersections.

Description of half-plane intersection

Intersections of half-planes are convex sets that can be both bounded and unbounded. We exclude the case that among given half-planes there are two opposite to each other. In this case, the intersection would be a subset of their common line, and this would lead to a one-dimensional task of the intersection of half-lines on the line.

If the intersection is bounded and $2$-dimensional, it is a convex polygon and we can describe it using a double-connected edge list with two faces, one bounded and one unbounded. In case the intersection is unbounded, we need to modify this description. For this purpose, we will use a lexicographic arrangement of points in the plane defined as follows:

Let us consider a non-empty convex set $ C $, which is the intersection of the half-planes and is not a subset of a line. There is just one of the following options:

1. The set C has a maximum point $p$ and a minimum point $q$ in the lexicographic arrangement. They both lie on the boundary and divide it into the left and right parts, abbreviated to the left and right boundaries. Each of these is a polygonal chain determined by the sequence of vertices and segments. We denote these sequences $L(C)$ and $P(C)$, respectively.
   
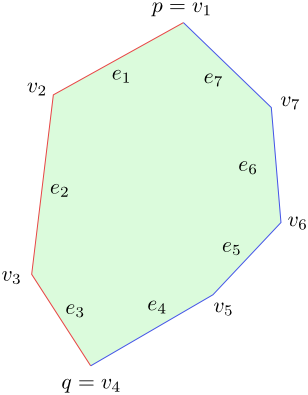
   Figure 5.1
   The left boundary of $C$ is $L(C)=(p=v_1,e_1,v_2,e_2,v_3,e_3,q=v_4)$, the right boundary is $P(C)=(p=v_1,e_7,v_7,e_6,v_6,e_5, v_5,e_4,q=v_4)$.
2. The set $C$ contains the maximum point $p$ but does not contain the minimum point. In this case the point $p$ divides the boundary of $C$ again into two parts, left and right. Each of them is determined by a sequence of vertices and segments terminated by a half-line.
   
   Figure 5.2
   The left boundary $L(C)=(p=v_1,e_1,v_2,e_2,v_3,e_3)$, the right boundary $P(C)=(p=v_1,e_7,v_7,e_6,v_6,e_5, v_5,e_4)$.
3. $C$ contains a minimum point $q$ but does not have a maximum point. In this case $q$ divides the boundary again into two parts, left and right. These are sequences, starting with a half-line followed by vertices and segments.
   
   Figure 5.3
   $L(C)=(e_1,v_2,e_2,v_3,e_3,q=v_4)$, $P(C)=(e_7,v_7,e_6,v_6,e_5, v_5,e_4,q=v_4)$.
4. The set $C$ has neither a maximum point nor a minimum point. In this case, there are two possibilities. Either the boundary has left and right parts formed by parallel lines or the boundary has only one part, left or right. This is determined by a single line or a sequence beginning and ending with a half-line with a sequence of vertices and segments between them. We will speak about the other part of the boundary as empty.
   
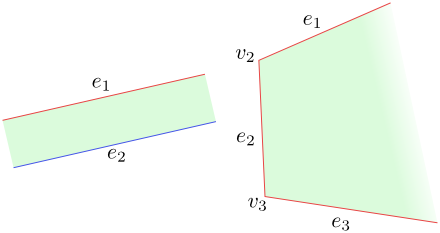
   Figure 5.4
   Left: $L(C)=(e_1)$, $L(C)=(e_2)$. Right: $L(C)=(e_1,v_2,e_2,v_3,e_3)$, $P(C)=(\ )$.

Algorithm for half-plane intersection

Let $C_1$ and $C_2$ be convex sets that have been created as intersections of disjoint sets of half-planes. Therefore they are determined by their left and right boundaries. We will describe an algorithm which will create two sequences describing the left and right boundary of the intersection $C_1\cap C_2$ out of the sequences $L(C_1)$, $P(C_1)$, $L(C_2)$, $P(C_2)$.

To do this, it is sufficient to realize that the vertices on the left boundary of $C_1\cap C_2$ are the following:

• vertices of $L(C_1)$, which lie inside $C_2$,
• vertices of $L(C_2)$, which lie inside $C_1$,
• points of intersection of the left boundaries of $C_1$ and $C_2$,
• points of intersection of the left boundary of $C_i$ and the right boundary of $C_j$ for $i\ne j$. They form in the given lexicographic order a maximal or a minimal vertex in $L(C_1\cap C_2)$.

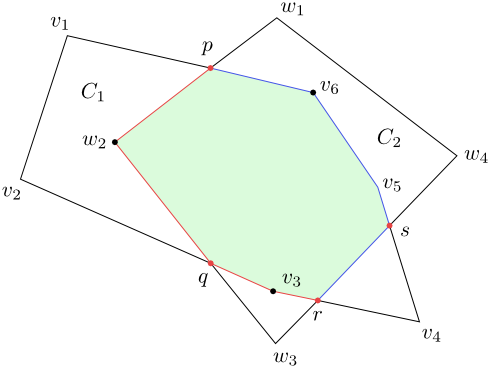
Figure 5.5
The vertices on the left boundary of the intersections $C_1\cap C_2$ are $p$ -- the point of the intersection of the left boundary of $C_2$ and the right boundary of $C_1$, $w_2\in L(C_2)$ lying inside $C_1$, $q$ -- the point of the intersection of the left boundaries, $v_3\in L(C_1)$ lying inside $C_2$ and $r$ -- the point of the intersection of the left boundary of $C_1$ and the right boundary of $C_2$.

Analogously, the points of the right boundary of $C_1\cap C_2$ are:

• vertices of $P(C_1)$ lying inside $C_2$,
• vertices of $L(C_2)$ lying inside $C_1$,
• points of intersection of the right boundaries of $C_1$ and $C_2$,
• points of intersection of the left boundary of $C_i$ and the right boundary of $C_j$ for $i\ne j$ They are maximal or minimal vertices of $P(C_1\cap C_2)$.

To create lists $L(C_1\cap C_2)$ and $P(C_1\cap C_2)$ we have to select the appropriate vertices of $ C_1 $ and $ C_2 $, to calculate the intersections of the boundaries and to organize chosen vertices lexicographically. Our algorithm will be similar to the algorithm for segment intersection in Chapter 1. So we use again sweep line method.

Events will be the vertices of $C_1$ and $C_2$ and the calculated intersections of boundaries. At the beginning of the algorithm, we set the boundary vertices lexicographically into the queue. Because the vertices are already arranged at both left and right boundaries, the creation of the queue takes time proportional to the number of vertices. Gradually, we will include the calculated intersections of boundaries into the event queue. Since we know on which segments or half-lines these intersections lie, their queuing will take only a constant time.

If neither of the convex sets $C_1$ and $C_2$ have a maximum point, we calculate the intersections of the half-lines that begin the left and right boundaries of both sets and we will place the obtained points into the queue. Since $C_1$ and $C_2$ are intersections of disjoint sets of half-planes, the set of the boundary intersections will be finite.

Horizontal sweep line $l$ moves from top to bottom. It starts at a position above the highest event. For every event we will record on which boundary it lies, and which lines, half-lines or segments pass through it. (For each of the three types of objects we will use a common notation edge.) We will also record the order in which the edges of each boundary cross the sweep line. Since there are no more than four edges crossing the sweep line, there is no need to keep the order in a binary balanced tree. When passing the event $v$, we perform the following actions:

• We include or do not include the event $v$ as a vertex in the sequence $L(C_1\cap C_2)$ or $P(C_1\cap C_2)$ using criteria given above.
• If $v$ is the first event in the left or right boundary of the intersection, and if there are some half-lines going upwards from it, we decide which one will be in the right and the left boundary of the intersection.
  
  Figure 5.6
  The vertex $v$ is the first event in $L(C_1\cap C_2)$. The half-line $f_1$ will be a part of $L(C_1\cap C_2)$ above $v$, and hence $L(C_1\cap C_2)=(f_1,v,\dots)$.
• We decide which of the edges going downwards from the event $v$ is in the left and which is in the right boundary of the intersection.
  
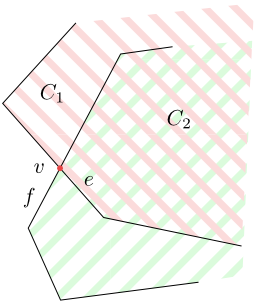
  Figure 5.7
  The edges $e$ and $f$ are going down the event $v\in L(C_1\cap C_2)$. The edge $e$ will be included in $L(C_1\cap C_2)$ below the event $v$, while $f$ is not any more a part of the boundary below $v$.
• We compute the intersection of the left edge $e_l$ originating from the event $v$ downwards with the adjacent left edge $s_l$ of the boundary of the second set, and the intersection of the right edge $e_p$ originating from the event $v$ downwards with the adjacent right edge $s_p$ of the boundary of the second set. If intersections exist and lie below $v$, we put them in the queue.
  
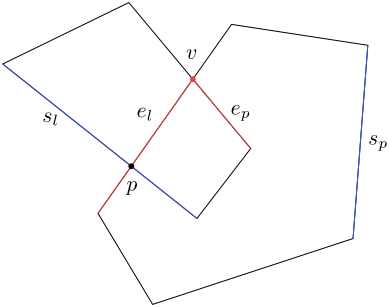
  Figure 5.8
  The choice of edges $e_l$, $e_p$, $s_l$, $s_p$ for the sweep line below the event $v$. We put the point $p=e_l\cap s_l$ in the queue. The intersection $e_p\cap s_p$ is empty.
• If the event $v$ is the minimum vertex of the left and right boundary of the intersection, we will remove all events from the queue as the description of both boundaries of the intersection is already complete. Otherwise, only the event $v$ is removed from the queue.

The algorithm ends when the queue is empty.

Pseudocodes and their running time

The intersection of two convex sets can be obtained in this way:

The passage of the sweep line through an event is recorded in the pseudocode:

The running time of the algorithm from the last pseudocode is constant. Let the convex sets $C_1$ and $C_2$ have $n_1$ and $n_2$ vertices, respectively. Then the running time of the algorithm from the pseudocode IntersectionOfTwo($C_1,C_2$) is $O(n_1+n_2)$.

The running time $T(n)$ of the whole algorithm for the computation of the intersection of $n$ half-planes is given by the recurrent relation

This leads to the resulting running time

Animation

An example of the computation of the intersection of two convex sets $C_1$ and $C_2$ according to the algorithms described by the second and the third pseudocodes is captured in the following animation.