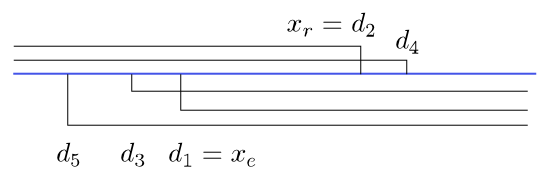Linear programming

Introduction

For a given linear function $f:\R^2\to \R$:

and a given set of $n$ half-planes $H = \{ h_1, h_2, \dots , h_n\}$ we want to find a point in the intersection of these half-planes

at which the function $f$ reaches its maximum. Half-planes $h_i$ are described as sets of points satisfying the inequalities

This problem is sometimes called linear program.

What is the geometric significance of this task? The function $f$ is determined by a vector $\vec{c}=(c_1,c_2)$. $f$ reaches the same value $k\in \R$ at all points of the line

The vector $\vec{c}$ is perpendicular to all such lines. Hence $f$ changes in the direction of the vector $\vec{c}$. Since $f(c_1,c_2)=c_1^2+c_2^2>0$, the function $f$ increases in the direction of $\vec{c}$. If $f$ achieves a maximum on the intersections of half-planes, then it is at the point that is extreme in the direction of vector $\vec{c}$.

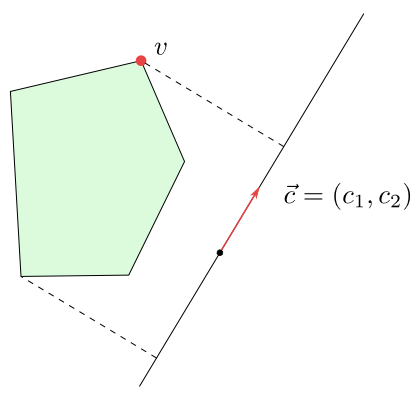
Figure 6.1
The point $v$ is the point where $f$ reaches its maximum on the given pentagon.

How about the solvability of our problem? There are the following options:

1. The intersection of half-planes is empty. We say that the linear program is infeasible.
2. There is just one point at which $f$ reaches its maximum.
   
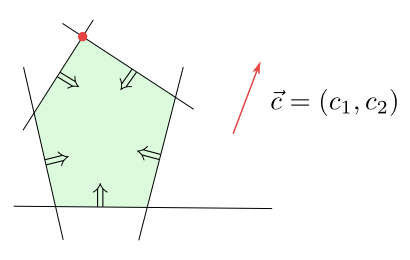
   Figure 6.2
   
3. There are infinitely many points at which $f$ reaches its maximum. These points form a line, a half-line or a segment.
   
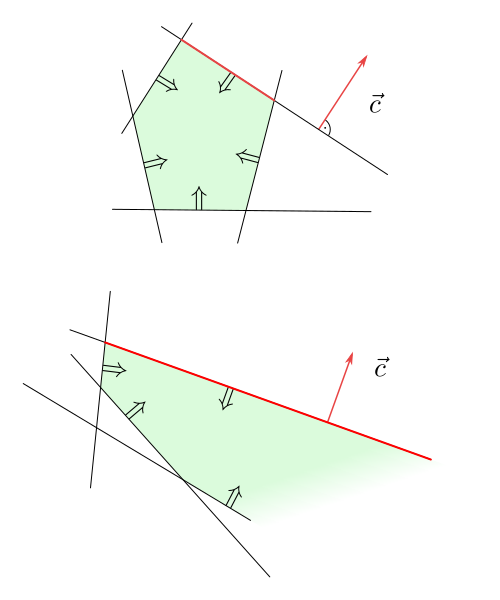
   Figure 6.3
   
4. The function $f$ is unbounded from above on the intersection of the half-planes. In this case, there is a half-line in the intersection of half-planes such that $f$ is growing along it.

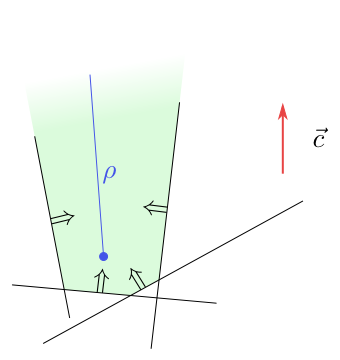
Figure 6.4
The function $f$ is growing along the half-line $\rho$.

Thus, the input of our algorithm will be a nonzero vector $\vec{c}$ and half-planes $ h_1, h_2, \dots, h_n $ given by inequalities (\ref{hp}). The output format will be one of the following:

1. Information that the intersection of half-planes is empty (linear program is infeasable) together with three chosen half-planes $h_i$, $h_j$, $h_k$ such that $$h_i\cap h_j\cap h_k=\emptyset .$$
2. One point in the intersection at which $f$ reaches its maximum. If there are more such points, it will be that one which is minimal in a chosen lexicographic arrangement. We will say, that this point is optimal for $f$ on the intersection of half-planes.
3. Information that $f$ does not achieve its maximum in the intersection together with a half-line which is contained in the intersection and along which $f$ is growing.

One-dimensional linear program

The problem of linear programming can be formulated in any dimension. In dimension 1, solving this task is especially easy, and our algorithm for resolving a two-dimensional problem will use solutions of one-dimensional problems in several steps.

A one-dimensional problem deals with finding $x\in\R$ at which the function

reaches its maximum under the conditions

for $i=1,2,\dots,n$. Let $I=\{i;a_i\gt 0\}$ and $J=\{j;a_j\lt 0\}$. After dividing $i$-th inequality by $a_i$ we obtain

Let

There are the following options:

1. $x_r\lt x_l$. Then the intersection of half-lines determined by the inequalities is empty.
2. $x_l\le x_r\lt \infty$ and $c\gt 0$. In this case, $f$ has a maximum at the point $x_r$.
3. $-\infty\lt x_l\le x_r$ and $c\lt 0$. In this case, $f$ has a maximum at the point $x_l$.
4. If $x_r=\infty$ and $c\gt 0$ or $x_l=-\infty$ and $c\lt 0$, the intersection of half-lines is a half-line along which the function $f$ is growing.

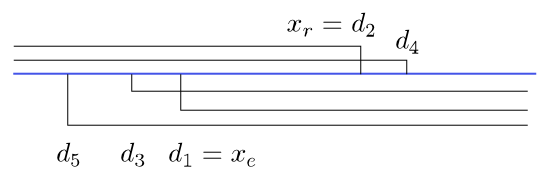
Figure 6.5
Specifying $x_l$ and $x_r$ if $I=\{2,4\}$ a $J=\{1,3,5\}$.

It can be seen from the previous procedure that solving one-dimensional linear program with $n$ inequalities means to find a maximum or a minimum of a set of numbers that has at most $n$ elements or to show that the set is empty or unbounded from one side. Thus, the running time of such an algorithm is $O(n)$.

Bounded linear program in the plane

First we show how to solve the problem of linear programming in the plane if we are guaranteed that the function $f$ is bounded from above on the intersection of half-planes.

Let us assume that there are two half-planes, denote them for simplicity $h_1$ and $h_2$, such that $f$ is bounded from above on the intersection $h_1\cap h_2$. In addition, assume that this intersection is not a half-plane.

Then $f$ has a maximum on $h_1\cap h_2$ at the intersection point $v_2$ of the boundary lines $l_1$ and $l_2$ of the half-planes. This is either a single point in which $f$ reaches its maximum or, if there are more such points, it is the point minimal in a suitable lexicographic arrangement.

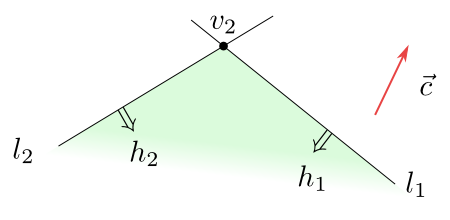
Figure 6.6
A function $f$ bounded on $h_1\cap h_2$ has a maximum in the point $v_2$.

Our algorithm for finding a solution of bounded linear program will be incremental. Starting with a known optimal point of $f$ on $C_2 = h_1\cap h_2$ we want to find gradually optimal points

If $C_i$ is not empty, it means that

1. the function $f$ reaches its maximum on the set $C_i$ at the point $v_i$,
2. from all points which satisfy the previous condition $v_i$ is minimal in a chosen lexicographic arrangement.

The following theorem says how to find $v_i$ if we know $v_ {i-1}$.

Theorem 6.1

If $v_{i-1}\in h_i$, then $v_i=v_{i-1}$.

If $v_ {i-1}\notin h_i$, then either $C_i =\emptyset$ or $v_i$ lies on the boundary line $ l_i$ of the half-plane $h_i$. In this case, we find $v_i$ as a solution of a one-dimensional linear program. If this one-dimensional program is infeasible, it gives us half-planes $h_k$, $h_j$ with $k, j \lt i $ such that $h_k\cap h_j\cap h_i=\emptyset$.

Proof

Obviously, $C_i\subseteq C_{i-1}$. If $v_{i-1}\in h_i$, then $v_{i-1}\in C_i$, and because $v_{i-1}$ is an optimal point for $f$ on $C_{i-1}$, it has to be also an optimal point for $f$ on $C_i$.

Now let $v_{i-1}\notin h_i$. If $C_i\ne\emptyset$, then $v_i\in h_i$ has to be different from $v_{i-1}$. Suppose that it does not lie on the boundary line $l_i$ of the half-plane $h_i$. Connect the points $v_{i-1}$ and $v_i$ by a segment. It has to intersect the line $l_i$. denote the intersection point by $q$ (see Figure 6.7). It holds

$$f(v_{i-1})\ge f(v_i).$$

Realize that the function $f$ is linear on the segment $[v_{i-1},v_i]$.

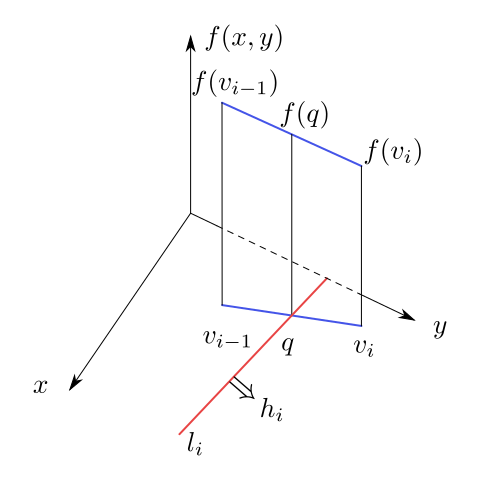
Figure 6.7
The function $f$ is linear on the segment $[v_{i-1},v_i]$.

If the inequality is strict, i.e. $f(v_{i-1})\gt f(v_i)$, we get from the linearity of $f$ that

$$f(v_{i-1})\gt f(q)\gt f(v_i).$$

See Figure 6.7. Moreover $q\in C_i$, which contradicts the fact that $f$ reaches its maximum on $C_i$ at $v_i$.

If $f(v_{i-1})=f(v_i)$, then also $f(v_{i-1})=f(q)$. In this case the chosen lexicographic order gives $v_{i-1}\lt q$, since $v_{i-1}$ is minimal (in lex. order) from all maximal points of $f$ on $C_{i-1}$. The lexicographic order of points on the segment $[v_{i-1},v_i]$ is linear, hence

$$v_{i-1}\lt q\lt v_i,$$

which is again a contradiction with the definition of $v_i$ as an optimal point of $f$ on $C_i$.

So we have proven that $v_i$ must lie on the line $l_i$. We will show how to find it. Let the coordinates of the point $v_i$ be $(x,y)$. Since the point lies on the line $l_i$, its coordinates satisfy the equation $a_{i1}x+a_{i2}y=b_i$ for this line. Suppose that $a_{i2}\ne 0$. Then we can compute $y$ using $x$

$$y=\frac{b_i-a_{i1}x}{a_{i2}}.$$

We are looking for a maximum of the function $f$ on $l_i$. On the line this function can be considered as a function of one variable

$$g(x)=c_1x+c_2\left(\frac{b_i-a_{i1}x}{a_{i2}}\right)= \left(c_1-c_2\frac{a_{i1}}{a_{i2}}\right)x -c_2\frac{b_i}{a_{i2}}.$$

The maximum point of the linear function $g$ does not depend on a constant, it is the same as the maximum point of the function

$$\widetilde g(x)=\left(c_1-c_2\frac{a_{i1}}{a_{i2}}\right)x=cx.$$

We look for a maximum point on the set $C_{i-1}\cap l_i$, which is given by inequalities

$$a_{j1}x+a_{j2}\left(\frac{b_i-a_{i1}x}{a_{i2}}\right)\le b_j$$

for $j=1,2,\dots,i-1$. These can be rewritten as

$$\left(a_{j1}-a_{j2}\frac{a_{i1}}{a_{i2}}\right)x\le b_j-a_{j2} \frac{b_i}{a_{i2}}.$$

We see, that to find the coordinates of the point $v_i,$ or to find that $C_i$ is empty in the case $v_{i-1}\notin h_i$ means to solve one dimensional linear program.

\(\Box\)

Running time of the algorithm for bounded linear program

The previous theorem determines an algorithm for solving the bounded linear program in the plane. The algorithm is described below in pseudocode \texttt{2dRandomizedLP} in lines 10 --17. If $v_{i-1}\in h_i$, the time needed to find $v_i$ is constant, and it is linear $O(i)$ if $v_{i-1}\notin h_i$. Since the solution of our task is to find a point $v_n$, the overall running time is at most

This running time is too high. In fact, it depends substantially in which order we take the half-planes $h_3,h_4,\dots,h_n$ for computation of $v_3, v_4, \dots, v_n$. Let us show it on the example from figures 6.8 and 6.9.

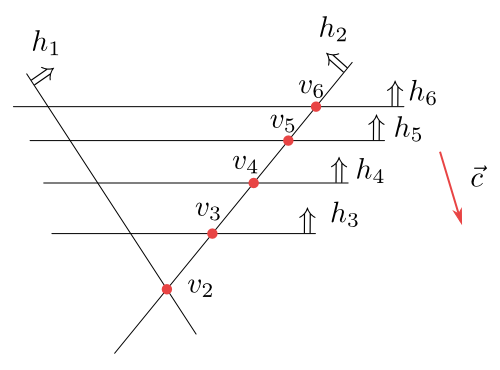
Figure 6.8

In this situation we take the order of half-planes in such a way that we get mutually different points $v_3$, $v_4$, $v_5$ and $v_6$. All these points are found as solutions of $1$-dimensional linear programs.

Next picture captures the same situation, but the individual half-planes are ordered in a different way such that $v_3=v_4=v_5=v_6$. So a $1$-dimensional linear program is used only for computing $v_3$.

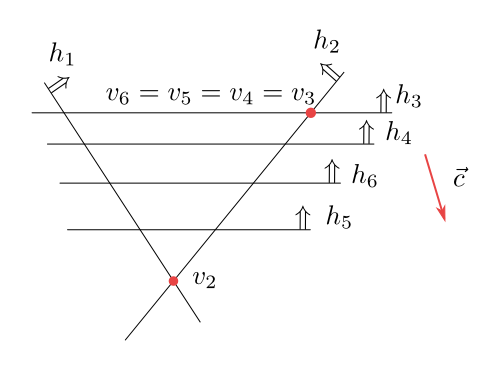
Figure 6.9

Randomized algorithm

Consider all possible orders of half-planes $h_3, h_4, \dots, h_n$. From the previous example, we can see that for different orders we get a different running time of the calculation. Randomized expected time is an average time of the calculation if we take into account all possible orders. In the case of linear program in the plane it will be much more favourable than $O(n^2)$. Taking the order of the half-planes $ h_3, h_4, \dots, h_n $ randomly, we can expect that the real time of calculation will match the expected randomized time. These considerations lead to a randomized algorithm. A random order of half-planes can be realized according to the following algorithm:

where the procedure RANDOM($k$) generates a random natural number from closed range $[1,k]$ in constant time.

The aim of this section is to prove following theorem

Unbounded linear program

To solve the general problem of linear programming we first need to determine if the function $f$ on the intersection of half-planes is at all bounded form above. The evidence for the unboundedness of $f$ is the existence of a half-line

in the intersection of half-planes on which $f$ is increasing with increasing $\lambda$. Here $p$ is a point in the intersection of half-planes and $\vec{d}$ is a suitable vector. If such a half-line exists, we say that the linear program $LP(H,\vec{c})$ is unbounded.

It is necessary and sufficient condition for $f$ being unbounded on $\rho,$ that the angle between vectors $\vec{c}$ a $\vec{d}$ is less than $90^o$, i.e. that the scalar product $\langle \vec{d}, \vec{c}\rangle\gt 0$. (Recall that $f$ increases in the direction of vector $\vec{c}$.)

Necessary condition for a half-line $\rho$ to lie in the half-plane $h_i$ is given by the fact that the vector $\vec{d}$ need not form with inner normal vector $\vec{\eta_i}$ of the half-plane $h_i$ an angle greater than $90^o$, i.e. that the scalar product $\langle \vec{d},\vec{\eta_i}\rangle\geq 0$. If the angle between $\vec{d}$ and $\vec{\eta_i}$ is greater that $90^o$, then any half-line with direction vector $\vec{d}$ leaves the half-line $h_i$. See the picture.

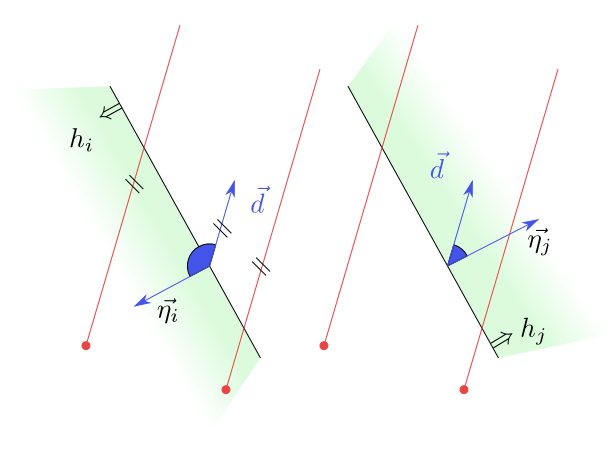
Figure 6.10
If $\langle \vec{d},\vec{\eta_i}\rangle\lt 0$, the half-plane $h_i$ does not contain any half-line with direction vector $\vec{d}$. If $\langle \vec{d},\vec{\eta_j}\rangle\geq 0$, then $h_j$ contains such half-lines.

An important role is also played by half-planes whose boundaries are parallel to the vector $\vec{d}$, i.e. those for which $\langle \vec{d},\vec{\eta_i}\rangle=0$. The half-line $\rho$ has to lie in their intersection, especially, this intersection has to be non-empty.

The previous considerations lead to the following assertion:

Substantial for us is how to find a vector $\vec{d}$ algorithmically, if it exists.

The whole algorithm is given in the following pseudocode

A detailed description of the algorithm including an implementation can be found (in Czech) in the bachelor thesis of Jan Kovář at the web page

https://is.muni.cz/auth/th/323609/prif_b/?lang=cs