---
title: "Řídící struktury"
author: "Michal Kvasnička"
documentclass: article
output:
html_document:
theme: cerulean
toc: yes
toc_float: yes
pdf_document: default
fontsize: 10pt
classoption: a4paper
---
# Řídící struktury
Zatím jsme předpokládali, že R provádí kód skriptu řádek po řádku. Někdy je však potřeba běh kódu různě modifikovat: některé řádky provést pouze, když je splněná určitá podmínka; jiné řádky provádět opakovaně; a\ někdy vypsat varování nebo zastavit běh skriptu s\ chybovým hlášením. Těmito problémy se budeme nyní zabývat.
V\ této kapitole se naučíte
- větvit kód pomocí podmínek
- opakovat kód pomocí cyklů
- vypisovat varování a zastavit kód chybovým hlášením
- že je možné chybová hlášení odchytit a vyřešit
## Větvení kódu {#sec:if}
Normálně R zpracovává skript tak, že vyhodnocuje řádek po řádku. Někdy to však nechceme. Některé řádky můžeme např.\ chtít provést pouze v\ případě, že je splněná nějaká podmínka. K\ tomu v\ R slouží podmínka\ `if`. Jediným argumentem `if` uvedeným v\ závorkách je podmínka, tj.\ výraz, který se musí vyhodnotit na logický vektor délky\ 1. Pokud je tento logický výraz splněný (má hodnotu\ `TRUE`), pak R vyhodnotí následující výraz. Pokud má logický výraz hodnotu\ `FALSE`, pak R následující výraz přeskočí. Ukažme si to na příkladu:
```r
x <- 1
y <- 2
if (x == 1)
print("O.K.: x je jedna!")
```
```
## [1] "O.K.: x je jedna!"
```
```r
if (y == 1)
print("O.K.: y je jedna!")
```
V\ tomto příkladě se první podmínka vyhodnotila jako pravdivá (`x` má opravdu hodnotu\ 1), takže R provedlo následující výraz a vypsalo "O.K.: x je jedna!". Naproti tomu druhá podmínka se vyhodnotila jako nepravdivá, takže druhý tiskový řádek R přeskočilo a nic nevypsalo. Všimněte si také, že k\ porovnání dvou hodnot se používá\ `==`.
Podmínka `if` se v\ R vztahuje vždy jen na jeden následující výraz. Pokud se má při splnění podmínky provést více než jeden řádek kódu, je třeba tyto řádky seskupit pomocí složených závorek (výrazy zabalené do složených závorek tvoří *blok* kódu):
```r
if (x == 1) {
a <- 5
print("O.K.: x je jedna!")
}
```
```
## [1] "O.K.: x je jedna!"
```
```r
a
```
```
## [1] 5
```
Nyní při splnění podmínky R nejdříve vloží do proměnné `a` hodnotu\ 5, a\ pak vypíše "O.K.: x je jedna!". Pokud by podmínka splněná nebyla, R\ by přeskočila oba řádky uvedené ve složených závorkách.
Někdy chceme, aby se část kódu provedla, pokud podmínka platí, zatímco jiná část kódu, pokud podmínka neplatí. K\ tomu slouží klauzule `else`. V\ následujícím kódu se vypíše "O.K.: y je jedna!", pokud je `y` rovno jedné, a\ "O.K.: y není jedna!", pokud se `y` od jedné liší.
```r
if (y == 1) {
print("O.K.: y je jedna!")
} else {
print("O.K.: y není jedna!")
}
```
```
## [1] "O.K.: y není jedna!"
```
Pozor: `else` musí být na stejném řádku, jako končící složená závorka nebo kód, který se provádí při splnění podmínky.
Podmínky lze libovolně řetězit, jak ukazuje následující příklad. Nejdříve se porovná `x` s\ jedničkou. Pokud se `x` rovná jedné, pak se vypíše "jedna" a kód pokračuje za poslední složenou závorkou. Pokud se `x` od jedničky liší, prozkoumá se, zda je větší než jedna. Pokud je, vypíše se "větší", pokud není, vypíše se "menší". (Pozor, tento kód nepočítá s\ tím, že by `x` mohlo mít i\ hodnotu `NA` nebo `NaN`\ -- vyzkoušejte si to.)
```r
x <- 1
if (x == 1) {
print("jedna")
} else if (x > 1) {
print("větší")
} else {
print("menší")
}
```
```
## [1] "jedna"
```
Je také možné vnořit jednu podmínku do jiné, jak ukazuje následující příklad:
```r
if (x > 0) {
if (x > 10) {
print("x je opravdu velké kladné.")
} else {
print("x je malé kladné")
}
}
```
```
## [1] "x je malé kladné"
```
Podmínky byste však neměli zanořovat příliš, protože by váš kód byl nepřehledný. (Všimněte si také, jak jsou v\ kódu odsazené řádky. R\ to nijak nevyžaduje. Je to však velmi užitečná konvence, která výrazně zvyšuje čitelnost kódu.)
Vlastní podmínka je vždy logická hodnota, přesněji logický vektor délky\ 1, který má hodnotu buď `TRUE` nebo `FALSE`, tj.\ ne `NA`. Pokud potřebujete složitější podmínku, musíte použít "zkratující" verze logických operátorů, viz oddíl\ \@ref(sec:data-types-log-oper). Pokud se má nějaký kus kódu provést pouze v\ případě, že platí `x` a zároveň `y` nebo `z`, zapíšeme to takto:
```r
if (x && (y || z)) {
...
}
```
Nápovědu k\ `if` (a\ dalším řídícím strukturám) získáte jedním z\ následujících způsobů:
```r
?`if`
help("if")
```
## Opakování kódu
V\ některých situacích potřebujeme, aby se nějaký kus kódu provedl vícekrát. K\ tomu slouží cykly. Existuje několik typů cyklů, které se liší podle toho, kolikrát se má daný kus kódu zopakovat.
### Cyklus se známým počtem opakování {#sec:for}
Nejjednodušší je cyklus `for`, který použijeme, když chceme nějaký kus kódu provést $x$-krát, kde $x$ je libovolné číslo známé před započetím cyklu. Cykly se používají nejčastěji k\ rekurzivním výpočtům. Řekněme např., že potřebujete nasimulovat data o\ náhodné procházce. Počáteční hodnota $y_1 = 0$, další hodnoty jsou konstruované rekurzivně jako $y_t = y_{t-1} + \epsilon_t$ pro $t>1$, kde $\epsilon_t$ je náhodná chyba vygenerovaná ze standardizovaného normálního rozdělení. Vektor tisíce pozorování je pak možné nasimulovat např.\ takto (výsledek ukazuje obrázek\ \@ref(fig:for-simul)):
```r
N <- 1000
y <- numeric(N)
y[1] <- 0 # zbytečné, ale pro přehlednost lepší
for (t in 2:N) # vlastní cyklus
y[t] <- y[t - 1] + rnorm(1) # kód, který se opakuje 999x
plot(y, type = "l") # vykreslení výsledku
```
Náš kód funguje takto: Nejdříve ze všeho vytvoříme celý vektor\ `y`. Sice bychom mohli začít vektorem délky\ 1 a postupně jej prodlužovat, to by však nutilo R neustále doalokovávat další paměť a výrazně by to zpomalilo výsledek. Proto je vždy lepší si dopředu předalokovat celou potřebnou paměť tím, že vytvoříme celé datové struktury ve velikosti, jakou bude mít výsledek výpočtu.
Vlastní cyklus začíná klíčovým slovem `for`. Proměnná\ `t` je *počítadlo* cyklu a postupně nabývá hodnot z\ vektoru uvedeného za klíčovým slovem\ `in`. Protože chceme, aby `t` postupně nabývalo hodnot\ 2 až 1\ 000, mohlo by se zdát jednodušší napsat `t in 2:1000`. To by však nebyl dobrý nápad. Nyní sice chceme simulovat právě tisíc pozorování, ale v\ budoucnu se možná rozhodneme jinak. Bezpečnější tak určitě je napsat `t in 2:N`, protože pak můžeme počet pozorování změnit na jediném řádku, a\ vše bude korektně fungovat.
Cyklus `for` proběhne v\ našem případě tak, že $N-1$\ krát spustí řádek `y[t] <- y[t - 1] + rnorm(1)`, přičemž počítadlo\ `t` bude postupně nabývat hodnot\ 2, 3, 4 atd., až se naplní celý vektor\ `y`. (Výsledek simulace záleží na generátoru pseudonáhodných čísel, takže bude pokaždé jiný.)
Stejně jako podmínka `if` i\ cyklus `for` provádí vždy jen jeden výraz. Pokud chceme, aby provedl více výrazů, pak musíme tyto výrazy uzavřít do složených závorek, tj.\ vytvořit z\ nich blok, jak ukazuje následující příklad:
```r
N <- 1000
y <- numeric(N)
z <- numeric(N)
for (t in 2:1000) {
y[t] <- y[t - 1] + rnorm(1)
z[t] <- sum(y[1:t])
}
```
Opět je vhodné kód výrazně odsadit, abychom zlepšili jeho čitelnost.
Někdy potřebujeme iterovat nad nějakým vektorem\ `y`. Na první pohled by se mohlo zdát, že počítadlo by mělo nabývat hodnot `t in 1:lenght(y)`. To však není dobrý nápad. Někdy se totiž může stát, že vektor\ `y` bude mít nulovou délku. Pak chceme, aby cyklus vůbec neproběhl. Pokud však počítadlo nastavíme výše uvedeným způsobem, cyklus překvapivě proběhne (a\ pravděpodobně skončí chybou). Důvod je ten, že dvojtečka má v\ cyklu svůj normální výraz konstruktoru vektorů. Pokud je `lenght(y)` rovno nule, pak má cyklus iterovat přes prvky vektoru `1:0`, což je vektor o\ délce\ 2 a hodnotách `c(1, 0)`. Správně tedy musí být počítadlo nastavené pomocí funkce `seq_along()` jako `t in seq_along(y)`.
Iterovat nad prvky nějakého vektoru\ `x` můžeme třemi různými způsoby: 1)\ můžeme iterovat nad indexy prvků, jako jsme to dělali v\ našem příkladu (použijeme např.\ `for (k in seq_along(x))`), 2)\ můžeme iterovat přímo nad hodnotami daného vektoru (použijeme `for (k in x)`) nebo 3)\ můžeme iterovat nad jmény prvků vektoru (použijeme `for (k in names(x))`). První způsob se používá nejčastěji, ale i další varianty jsou někdy užitečné.
Existují situace, kdy se bez cyklu `for` neobejdeme. V\ R se však tento cyklus používá mnohem méně než v\ jiných jazycích. Důvody jsou dva: Zaprvé, R\ je vektorizovaný jazyk se spoustou vektorizovaných funkcí, takže mnoho operací, které je v\ jiných jazycích nutné psát pomocí cyklu, v\ R vyřeší vektorizace. Dokonce i\ náš první příklad cyklu je vlastně zbytečný a simulaci je možné provést takto:
```r
N <- 1000
e <- c(0, rnorm(N - 1)) # simulace náhodné složky
y <- cumsum(e) # kumulativní součet
```
Za druhé, pro iteraci nad vektory má R jiný velmi silný nástroj, a\ to funkce typy `map()`, se kterými se seznámíte v\ kapitole\ \@ref(kap:iterace-nad-vektory).
Dokumentaci k\ cyklu `for` najdete pomocí `help("for")`.
### Cykly s neznámým počtem opakování
V\ některých situacích nevíme, kolikrát bude potřeba kus kódu opakovat. Pro tyto účely slouží dva standardní typy cyklů: cyklus `while` opakuje kus kódu, dokud je splněná nějaká podmínka; naproti tomu cyklus `repeat` opakuje kus kódu donekonečna s\ možností cyklus přerušit, pokud je nějaká podmínka splněná. Rozdíl mezi cykly spočívá v\ tom, kdy se podmínka vyhodnotí: v\ cyklu `while` se podmínka vyhodnocuje na začátku, takže cyklus nemusí proběhnout ani jednou; naproti tomu v\ cyklu `repeat` se podmínka vyhodnocuje v\ principu až na konci, takže cyklus vždy proběhne aspoň jednou. Tyto cykly se při datové analýze nepoužívají příliš často. Zato jsou velmi užitečné v\ simulacích, optimalizacích a podobných úlohách. Zde se podíváme pouze na jednodušší a častěji používaný cyklus `while`. Více se o\ obou cyklech můžete dozvědět z\ dokumentace (`help("while")`).
Použití cyklu `while` si ukážeme na následujícím příkladu: Předpokládejme, že chceme zjistit, kolikrát musíme hodit kostkou, než padne šestka. To můžeme provést např.\ následujícím kódem:
```r
pocet <- 0
kostka <- 0
while (kostka != 6) {
pocet <- pocet + 1
kostka <- sample(6, size = 1)
}
print(pocet)
```
```
## [1] 8
```
Skript funguje takto: nejdříve si vytvoříme proměnnou `pocet`, do které budeme shromažďovat uplynulý počet hodů. Dále vytvoříme proměnnou `kostka`, do které uložíme hod kostkou. Vlastní cyklus začíná klíčovým slovem `while`. V\ závorce za ním je podmínka, tj.\ výraz, který se musí vyhodnotit na logický vektor délky\ 1. Pokud je podmínka splněná (logický výraz se vyhodnotí na\ `TRUE`), vyhodnotí se výraz, který následuje. Protože chceme vyhodnotit dva výrazy, musíme je pomocí složených závorek uzavřít do bloku.
Při prvním průchodu cyklu je `kostka` rovna nule, proto se cyklus provede: počítadlo `pocet` se zvýší o\ 1 a "hodíme kostkou" (funkce `sample()` v\ našem případě vygeneruje náhodné celé číslo od\ 1 do\ 6). Pokud "padlo" jiné číslo než\ 6, cyklus proběhne znovu (počítadlo se zvýší o\ další\ 1 a znovu se hodí kostkou). To se opakuje, dokud je podmínka splněná (tj.\ `kostka` je různá od\ 6). Jakmile se `kostka` rovná šesti, cyklus už neproběhne a R\ přejde na vypsání hodnoty `pocet`. (Výsledek simulace záleží na generátoru pseudonáhodných čísel, takže bude pokaždé jiný.)
Podívejme se na jiný stylizovaný příklad. Řekněme, že chceme zjistit, pro jaký vstup z\ určitého intervalu nabývá nějaká funkce určité hodnoty. Aby byla úloha jednoduchá, budeme předpokládat, že funkce je monotónně rostoucí. V\ takovém případě můžeme použít primitivní algoritmus půlení intervalů. Jako funkci budeme v\ našem příkladu pro jednoduchost uvažovat přirozený logaritmus a budeme hledat takovou hodnotu\ $x$ z\ intervalu $[0, 10]$, pro kterou je $log(x) = 1$:
```r
hodnota <- 1
funkce <- log
dint <- 0
hint <- 10
tolerance <- 1e-10
chyba <- Inf
while (abs(chyba) > tolerance) {
vysledek <- (dint + hint) / 2
pokusna_hodnota <- funkce(vysledek)
if (pokusna_hodnota < hodnota)
dint <- vysledek
if (pokusna_hodnota > hodnota)
hint <- vysledek
chyba <- hodnota - pokusna_hodnota
}
vysledek
```
```
## [1] 2.718282
```
Nejprve jsme zadali hledanou hodnotu (`hodnota`), použitou funkci (`funkce`), horní a dolní mez prohledávaného intervalu (`dint` a `hint`) a toleranci (`tolerance`), se kterou má algoritmus pracovat. Zadali jsme i\ počáteční velikost chyby (`chyba`). Vlastní výpočet funguje takto: pokud je absolutní hodnota chyby větší než zadaná tolerance, provedeme úpravu mezí, a\ to tak, že 1.\ najdeme hodnotu uprostřed intervalu, 2.\ vyhodnotíme hodnotu funkce v\ tomto bodě, 3.\ pokud je výsledek nižší než požadovaná hodnota, posuneme dolní mez na úroveň středu intervalu; v\ opačném případě takto posuneme horní mez, 4.\ spočítáme velikost chyby. Cyklus upravuje meze tak dlouho, dokud není chyba menší než zadaná tolerance. Nakonec vypíšeme hledanou hodnotu, která zůstala v\ proměnné `vysledek`. Výsledek si můžeme snadno ověřit "zkouškou"; můžeme se také podívat, že chyba je opravdu menší než zadaná tolerance (protože pro přirozený logaritmus máme k\ dispozici inverzní funkci):
```r
log(vysledek)
```
```
## [1] 1
```
```r
exp(1) - vysledek
```
```
## [1] -1.064779e-10
```
Algoritmus je velmi rychlý, ale samozřejmě není příliš obecný: funguje jen pro monotonně rostoucí funkce. (R\ má naštěstí celou řadu funkcí, které dokážou numericky optimalizovat zadanou funkci.)
## Zastavení kódu a varování
Někdy je potřeba výpočet zastavit a vydat chybovou hlášku. Typicky to chcete udělat, když váš kód dostal špatný vstup. Řekněme např., že stahujete data z\ nějakého serveru a víte, že některá proměnná může mít jen určité úrovně. Převedete ji tedy na faktor a zkontrolujete, že žádná hodnota ve faktoru není `NA`, což by signalizovalo, že server změnil kódování úrovní. Pokud tedy ve vektoru najdete `NA`, chcete kód ukončit chybou, abyste zjistili, že musíte situaci řešit.
K\ zastavení běhu skriptu slouží funkce `stop()`: zastaví běh skriptu a jako chybovou hlášku vypíše svůj argument. Následující kód zastaví běh skriptu a vypíše chybovou hlášku, pokud `v` obsahuje řetězec:
```r
v <- "ahoj"
if (is.character(v))
stop("v je řetězec!")
```
```
## Error in eval(expr, envir, enclos): v je řetězec!
```
Jednodušší variantou předchozího kódu je použití funkce `stopifnot()`. Ta zastaví kód, pokud se zadaný výraz nevyhodnotí na\ `TRUE`. V\ tom případě se vypíše jako chybová hláška, že daný výraz není\ `TRUE`. Předchozí podmínku pak můžeme zapsat přibližně takto (všimněte si znaku\ `!`, který neguje zadaný výraz):
```r
stopifnot(!is.character(v))
```
```
## Error: !is.character(v) is not TRUE
```
Někdy problém není tak velký, že bychom chtěli běh skriptu zastavit. Chceme však upozornit uživatele (nejčastěji sami sebe), že někde nastal nějaký problém. R\ umí posílat dva typy signálů: zprávy (messages) a varování (warnings).
Zprávy je možné do konzoly vypsat pomocí funkce `message()`, varování pomocí funkce `warning()`. Obě tyto funkce vypíší do konzoly svůj argument:
```r
if (!is.list(v))
warning("Pozor: v není seznam!")
```
```
## Warning: Pozor: v není seznam!
```
Do konzoly je samozřejmě možné vypisovat i\ pomocí funkcí `print()`, `cat()` apod. Zprávy o\ běhu kódu však vypisujte raději pomocí `message()` a `warning()`: v\ RStudiu jsou barevně odlišené a je možné je snadno potlačit pomocí funkcí `suppressMessages()` a `suppressWarnings()`, pokud nejsou žádoucí, což v\ případě `print()` a spol. nejde.
## Odchycení chyb
Někdy potřebujeme napsat skript, který musí být rezistentní vůči chybám\ -- jeho běh nesmí skončit ani v\ případě, že chyba nastane. Typickým případem je situace, kdy stahujeme nějaká data ze sítě, např.\ z\ API Googlu, ale naše připojení k\ internetu je poruchové. Pak funkce, která stahuje data skončí chybou. My však nechceme, aby skript zhavaroval. Místo toho chceme chybu odchytit a nějak zpracovat, např.\ chvíli počkat, a\ pak se pokusit stáhnout data znovu.
Stejně jako většina pokročilých programovacích jazyků, i\ R má nástroje pro "zpracování výjimek". V\ R je zastupují funkce `try()` a `tryCatch()`. Pokud je budete někdy potřebovat použít, podívejte se do jejich dokumentace.
## Aplikace: simulace hry Hadi a žebříky
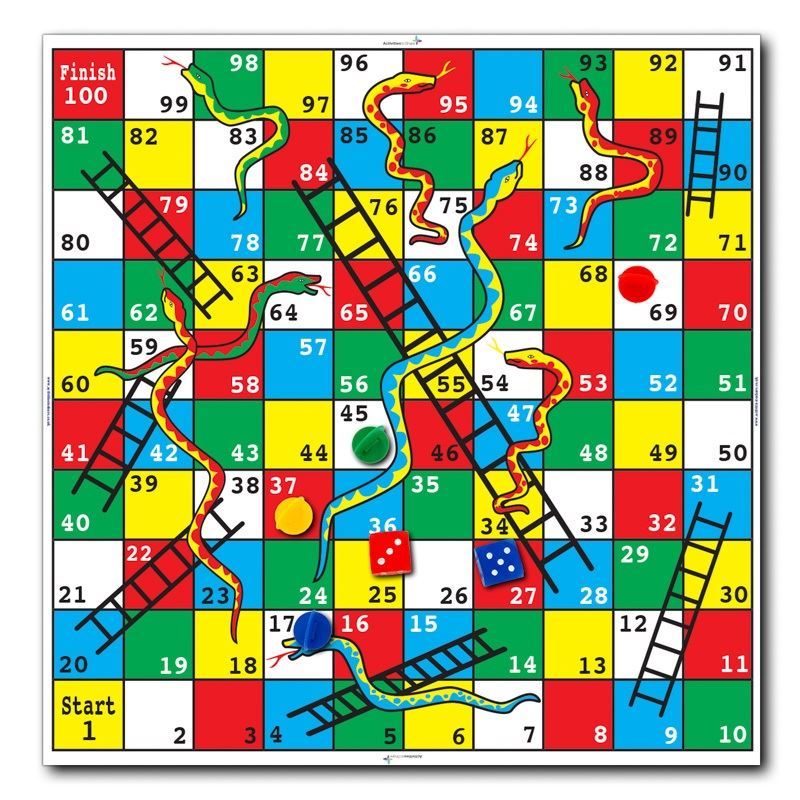
Existuje hra, kterou malé děti milují a jejich rodiče nenávidí: *Hadi a žebříky* (v\ originále *Snakes and ladders*). Pravidla hry jsou jednoduchá: každý hráč má právě jednu figurku, kterou postaví na první pole hry. Hráči se pak po řadě střídají v\ tom, kdo hází kostkou. Hráč, který právě hodil kostkou, posune svoji figurku o\ tolik polí, kolik mu na kostce padlo. Vítězem je ten hráč, který se jako první dostane na poslední, 100.\ pole. Hra je ozvláštněna speciálními poli: kdo šlápne na pole paty žebříku, ten se posune o\ daný počet polí dopředu ("vyjede po žebříku"), kdo však šlápne na hlavu hadovi, vrátí se o\ daný počet polí zpět ("sjede po hadovi"). Herní plán ukazuje obrázek\ \@ref(fig:ctrl-snakes-and-ladders)
Už asi tušíte, proč děti hru milují: vše je dáno jen náhodou, jejíž zvraty jsou kvůli umístění žebříků a hadů často veliké, takže poslední hráč se může pár tahy vyšvihnout do začátku pelotonu, zatímco dosud první hráč může snadno spadnout na konec. Navíc hra trvá opravdu dlouho. Asi je také jasné, proč rodiče hru naprosto nenávidí: vlastně se nejedná o\ hru! Vše je dáno náhodou, chybí jakákoli interakce mezi hráči a hra může trvat neskutečně dlouho (nekonečně dlouho, zdá se znuděnému rodiči). Člověče nezlob se je proti této hře posledním výkřikem moderních strategických her.
Naším cílem bude nasimulovat deset tisíc krát průběh hry a zjistit, jaké je rozdělení počtu hodů potřebných k\ ukončení hry. Pro jednoduchost si problém zjednodušíme tak, že budeme uvažovat jen jednoho hráče. Dále budeme předpokládat, že k\ vítězství ve hře není potřeba se přesně trefit na 100.\ pole, ale že stačí se dostat na ně nebo za ně.
Následně použijeme data ze simulace s\ jedním hráčem k\ odhadu počtu tahů, které potřebují k\ ukončení hry dva nebo tři hráči. Pro jednoduchost budeme předpokládat, že hra končí ve chvíli, kdy jeden z\ hráčů vyhrál, tj.\ že se nedohrává až do konce. (Nápověda: hráči nijak neinteragují.)
Začneme tím, že si první úkol rozebereme. Budeme potřebovat dvě proměnné: Zaprvé, proměnnou `panacek`, ve které budeme mít uložené pole, na kterém panáček stojí. Na začátku bude mít tato proměnná hodnotu\ 1.
Zadruhé, budeme potřebovat proměnnou `hody`, kam si budeme zaznamenávat, kolik hodů už proběhlo. Počáteční hodnota této proměnné je samozřejmě\ 0.
Každá jednotlivá hra bude spočívat v\ opakování tří kroků: 1.\ Hodíme kostkou a posuneme panáčka o\ tolik kroků, o\ kolik bude potřeba. 2.\ Až se panáček posune, zkontrolujeme, na jakém poli figurka stojí: pokud je to žebřík, posuneme jej nahoru, pokud had, posuneme jej dolů, jinak jej necháme na místě. 3.\ Zvýšíme hodnotu počítadla hodů o\ 1. Tyto tři kroky budeme opakovat tak dlouho, dokud panáček nebude stát na poli 100 nebo za ním. Na konci si zapamatujeme, kolik hodů bylo k\ ukončení hry potřeba. Kód pro jednu hru tak bude vypadat nějak takto:
```r
panacek <- 1L
hod <- 0L
while (panacek < 100L) {
hod <- hod + 1L
panacek <- panacek + sample(6, size = 1)
panacek <- pole[panacek]
}
```
Funkce `sample(6, size = 1)` na předposledním řádku cyklu vrátí náhodné číslo z\ oboru 1,\ 2,\ ...,\ 6 (tj.\ simuluje hod kostkou). Otázkou je, jak vyřešíme hady a žebříky. To je možné udělat celou řadů způsobů. Můžeme např.\ pro každého hada a žebřík napsat podmínku typu
```r
if (panacek == 4)
panacek <- 14
```
která posune panáčka ze 4.\ na 14.\ pole (1.\ žebřík). Já preferuji poněkud globálnější přístup, který ukazuje poslední řádek cyklu: vytvoříme vektor `pole`, který pro každé herní políčko řekne, kam se má panáček posunout. Pokud dané pole neobsahuje ani hada, ani žebřík, bude obsahovat svůj vlastní index. Proměnnou pole vytvoříme např.\ takto:
```r
# inicializace hracího pole
pole <- 1:105
# -- žebříky
pole[4] <- 14L
pole[9] <- 31L
pole[20] <- 38L
pole[28] <- 84L
pole[40] <- 59L
pole[63] <- 81L
pole[71] <- 91L
# -- hadi
pole[17] <- 7L
pole[54] <- 34L
pole[62] <- 18L
pole[64] <- 60L
pole[87] <- 24L
pole[93] <- 73L
pole[95] <- 75L
pole[98] <- 78L
```
Nejdříve inicializujeme `pole` tak, aby platilo `pole[i] = i`, tj.\ aby hráč, který na toto pole šlápne, na něm i\ zůstal. Pak přidáme žebříky a hady. Všimněte si, že pole nemá 100\ prvků, ale\ 105. To je proto, že panáček se může díky hodu kostkou dostat za 100.\ `pole`. Pokud bychom je neinicializovali, skript by skončil chybou. (Náš přístup k\ poli je poněkud nedbalý\ -- pokud by se hrací pole zvětšilo, rostly by nároky na paměť počítače. Hra *Hadi a žebříky* se však, doufejme, nikdy nezvětší.)
Nyní tedy umíme zahrát jednu hru. Zbývá nám ji ještě deset tisíc krát zopakovat. To provedeme takto:
```r
# počet simulací
N <- 1e4
# ... sem se vloží inicializace hracího pole...
# alokace vektoru výsledků
vysledek <- rep(NA, N)
# vlastní simulace
for (k in seq_len(N)) {
# ... sem se vloží kód pro jednu hru
vysledek[k] <- hod
}
```
Nyní nám stačí celý kód spustit a vypsat popisné statistiky pomocí funkce `summary()` a případně vykreslit histogram rozdělení počtu hodů pomocí funkce `hist()` (v\ kapitole \@ref(kap:ggplot2) se naučíte kreslit hezčí grafy). Celý kód tedy vypadá takto:
```r
# počet simulací
N <- 1e4
# inicializace hracího pole
pole <- 1:105
# -- žebříky
pole[4] <- 14L
pole[9] <- 31L
pole[20] <- 38L
pole[28] <- 84L
pole[40] <- 59L
pole[63] <- 81L
pole[71] <- 91L
# -- hadi
pole[17] <- 7L
pole[54] <- 34L
pole[62] <- 18L
pole[64] <- 60L
pole[87] <- 24L
pole[93] <- 73L
pole[95] <- 75L
pole[98] <- 78L
# alokace vektoru výsledků
vysledek <- rep(NA, N)
# vlastní simulace
for (k in seq_len(N)) {
panacek <- 1L
hod <- 0L
while (panacek < 100L) {
hod <- hod + 1L
panacek <- panacek + sample(6, size = 1)
panacek <- pole[panacek]
}
vysledek[k] <- hod
}
```
```r
# shrnutí výsledků
summary(vysledek)
hist(vysledek)
```
Výsledky simulace ukazuje tabulka \@ref(tab:snakes-and-ladders1t), rozdělení počtu hodů potřebných k\ ukončení hry ukazuje obrázek\ \@ref(fig:snakes-and-ladders1f). Průměrný počet hodů, potřebný k\ dokončení při v\ jednom hráči, je 48.2545; ve čtvrtině her však nebude stačit ani 61 hodů.
(ref:snakes-and-ladders1r) Souhrnné statistiky počtu hodů potřebných k\ ukončení hry *Hadi a žebříky*, pokud hraje jeden hráč.
Table: (\#tab:snakes-and-ladders1t)(ref:snakes-and-ladders1r)
Min. 1st Qu. Median Mean 3rd Qu. Max.
----- -------- ------- -------- -------- -----
7 25 39 48.2545 61 327
Naším druhým úkolem je zjistit, kolik hodů kostkou by bylo potřeba, kdyby hru hrálo $M > 1$ hráčů. Na první pohled by se mohlo zdát, že potřebujeme celou naši simulaci přepsat tak, aby v\ rámci každé dílčí hry hrálo $M$\ hráčů. To však vůbec není potřeba, a\ to díky tomu, že hráči ve hře nijak neinteragují. Pokud tedy hrají tři hráči, je to stejné, jako by nezávisle na sobě hráli tři hráči. Hra skončí, když kterýkoli z\ nich dojde na 100.\ políčko. Kolik hodů k\ tomu potřebuje, to máme uložené v\ proměnné `vysledek`. Přibližně správný odhad tedy můžeme získat tak, že z\ vektoru výsledek náhodně vybereme tři hodnoty (s\ opakováním) a z\ nich vezmeme nejmenší číslo (stanovili jsme si, že hra končí, když vyhrál první hráč). Tak zjistíme, kolikrát by musel hodit vítězný hráč. Jeho počet hodů musíme samozřejmě vynásobit počtem hráčů, protože ve skutečnosti každý hráč musel hodit tolikrát.
Pokud jsme estéti, můžeme ještě provést jistou korekci pro posledního hráče. Řekněme, že vítězný hráč hodil právě $L$-krát. Pokud hrají tři hráči, pak máme tři možnosti: 1)\ Vítězný hráč začínal hru; pak je celkový počet hodů $(L - 1) \times 3 + 1$. 2)\ Vítězný hráč házel jako druhý; pak je celkový počet hodů $(L - 1) \times 3 + 2$. A\ konečně 3)\ vítězný hráč házel jako poslední; pak je celkový počet hodů $3L$. Každá z\ těchto možností se stala právě s\ pravděpodobností\ $1/3$. Pokud tedy hrají tři hráči, musíme od jednoduchého výsledku získaného jako trojnásobek počtu hodů vítězného hráče odečíst s\ pravděpodobností\ $1/3$ dvojku, s\ pravděpodobností\ $1/3$ jedničku a s\ pravděpodobností\ $1/3$ nulu. Obecně musíme odečíst $(M - 1) / 2$.
Tímto postupem zjistíme, jak dlouho by hrálo $M$\ hráčů v\ jedné konkrétní hře. Výsledkem je tedy opět náhodné číslo. Simulaci opět potřebujeme zopakovat (řekněme 10\ 000\ krát), abychom dostali rozdělení počtu hodů.
Celou simulaci provedeme snadno takto:
```r
# počet hráčů
hracu <- 3
# alokace vektorů výsledků
vysledek2 <- rep(NA, N)
# korekce počtu tahů (hráč, který hru ukončil nemusel hrát jako poslední)
korekce <- (hracu - 1) / 2
# vlastní simulace (bootstrap)
for (k in seq_len(N)) {
vyber <- sample(N, size = hracu, replace = TRUE)
vysledek2[k] <- hracu * min(vysledek[vyber]) - korekce
}
```
Nejdříve do proměnné `hracu` uložíme počet hráčů, v\ našem případě\ 3. Následně si předalokujeme vektor pro uložení výsledků simulace a spočítáme správnou korekci. Vlastní simulaci zopakujeme\ $N$-krát (10\ 000\ krát). Při každé jednotlivé simulaci vybereme pomocí funkce `sample()` tři náhodná čísla z\ rozsahu\ $1, 2, \ldots, N$ s\ opakováním. Tato čísla použijeme jako indexy k\ výběru tří náhodných délek hry z\ vektoru `vysledek` a s\ jejich pomocí spočítáme střední dobu délky hry tří hráčů. Nakonec se podíváme na souhrnné statistiky pomocí funkce `summary()` a na histogram pomocí funkce\ `hist()`.
Tabulka \@ref(tab:snakes-and-ladders2t) ukazuje základní statistiku pro tři hráče. Průměrný počet nutných hodů při třech hráčích vzrostl z\ 48.2545 na 75.6008; ve čtvrtině her však nebude stačit ani 92 hodů. Obrázek\ \@ref(fig:snakes-and-ladders2f) ukazuje srovnání distribuce počtu hodů při jednom a při třech hráčích. Takové obrázky se naučíte kreslit v\ kapitole\ \@ref(kap:ggplot2).
(ref:snakes-and-ladders2r) Souhrnné statistiky počtu hodů potřebných k\ ukončení hry *Hadi a žebříky*, pokud hrají tři hráči.
Table: (\#tab:snakes-and-ladders2t)(ref:snakes-and-ladders2r)
Min. 1st Qu. Median Mean 3rd Qu. Max.
----- -------- ------- -------- -------- -----
20 50 68 75.6008 92 311
Náš odhad distribuce počtu hodů nebude při opakování 10\ 000\ krát úplně přesný a při každém spuštění vrátí poněkud odlišné výsledky. Zvýšení přesnosti můžete dosáhnout zvýšením počtu simulací, např.\ na milion. Náš kód je možné ještě zobecnit a doladit tím, že je přepíšeme pomocí funkcí (viz kapitola\ \@ref(kap:funkce)) a funkce\ `map_dbl()` (viz kapitola\ \@ref(kap:iterace-nad-vektory)).