18.3 Odhad modelu

Při volání estimační funkce se dohromady spojí všechny tři komponenty: modelová specifikace, data a estimátor.

Základní estimační funkcí je lm(), určená pro odhad lineárních modelů. Funkce přijímá celou řadu parametrů:

lm(formula, data, subset, weights, na.action, method = "qr", 
    model = TRUE, x = FALSE, y = FALSE, qr = TRUE, singular.ok = TRUE, 
    contrasts = NULL, offset, ...)

Mezi základní patří:

  • formula je objekt třídy “formula”, který obsahuje symbolický popis rovnice, jejíž parametry se mají odhadnout.
  • data je tabulka (data.frame) která obsahuje data, která se mají použít. Jména sloupců v tabulce musí odpovídat proměnným použitým v parametru formula. Datová tabulka nemusí být specifikována. Pokud je tento parametr prázdný, potom R interpretuje jména v modelu jako jména proměnných z prostředí, ze kterého je funkce lm() volána.
  • subset je nepovinný parametr, který určuje, které pozorování (řádky) se mají použít pro odhad
  • weights je vektor vah. Pokud není zadán je pro odhad použit obyčejný OLS estimátor, ve kterém mají všechna pozorování stejnou váhu. V případě zadání vah je vráceno WLS.

Struktura a forma těchto základních vstupů je typicky shodná právě s lm().

18.3.1 Vytvoření matice plánu

Pro odhad použijeme model v následující specifikaci:

model <- Weight ~ Height + Age + I(Age^2) + Sex

Proměnné Weight, Height a Age jsou numerické spojité proměnné. Proměnná Sex je zcela jiný případ. Jsou to kategoriální proměnná, se dvěma úrovněmi (M – muž, F – žena). Taková proměnná nemůže vstoupit do regrese přímo. Je nutné ji transformovat na matici nul a jedniček. Transformovaná matice bude mít vždy o jeden sloupec méně, než kolik má transformovaná proměnná úrovní.

Estimační funkce si všechny vstupní faktory transformuje sama pomocí interního volání funkce model.matrix(). V rámci volání tento funkce se provedou i požadované transformace dat. V případě našeho modelu vytvoření druhé mocniny věku. Výsledkem volání model.matrix() je tedy matice plánu:

model.matrix(model, data = oly12) %>% head()
##   (Intercept) Height Age I(Age^2) SexM
## 1           1   1.70  23      529    1
## 2           1   1.93  33     1089    1
## 3           1   1.87  30      900    1
## 4           1   1.78  26      676    0
## 5           1   1.82  27      729    1
## 6           1   1.82  30      900    0

Funkce model.matrix() provede požadované transformace numerických proměnných (přidán sloupec I(Age^2)) a pokud najde jinou než numerickou proměnnou (factor) provede jejich transformaci do matice binárních proměnných. Při této transformaci postupuje následovně. Prohlédne si faktor a určí referenční úroveň (level). Ta nebude ve výsledné matici obsažena, pokud by byla, model by nešel odhadnout. Pro každou zbývající úroveň vytvoří vektor, který nabývá hodnoty 1 pro pozorování s danou úrovní faktoru. V příkladu výše si model.frame() vybral jako referenční úroveň hodnotu F a vytvořil vektor SexM, který nabývá hodnoty 1 pro muže a 0 ve všech ostatních případech.

Pokud by byla vstupní kategoriální proměnná třídy character, potom by ji model.frame()nejprve transformoval na factor a pokračoval tak, jak je popsáno výše. Toto chování může být motivem pro to, aby uživatel sám provedl konverzi na faktor. Třída faktor totiž umožňuje nastavit, která úroveň má být použita jako referenční. Toho můžeme docílit pomocí několika cest.

První variantou je konverze do factor s pomocí base::factor(). Tato funkce umožňuje uživateli zadat vektor možných úrovní. První z nich se potom nastaví jako referenční:

factor(Sex$oly12, c("M","F"))

Tento postup lze aplikovat i na proměnné, které již jsou factor. Nevýhodou je nutnost zadávat všechny úrovně. Podobnou variantou je použití funkce forcats::as_factor(). Ta má vlastnost, že pořadí úrovní stanoví podle podle pořadí jejich výskytu v transformovaném vektoru. Problém této funkce je, že pracuje zvláštně s chybějícími hodnotami. (To se pravděpodobně bude během vývoje balíku ještě měnit.)

Další principiálně odlišnou variantou je nastavení referenční úrovně pomocí funkce stats::relevel() (alternativně forcats::fct_relevel()). Ta umožňuje prosté nastavení referenční úrovně:

factor(Sex$oly12) %>% relevel("M")

Po změně referenční úrovně bude výsledek následující:

oly12 %>% 
  mutate(
    Sex = factor(Sex) %>% relevel("M")
  ) %>% 
  model.matrix(model,.) %>% 
  head()
##   (Intercept) Height Age I(Age^2) SexF
## 1           1   1.70  23      529    0
## 2           1   1.93  33     1089    0
## 3           1   1.87  30      900    0
## 4           1   1.78  26      676    1
## 5           1   1.82  27      729    0
## 6           1   1.82  30      900    1

Zejména v rámci průzkumu dat je zajímavá varianta provést konverzi na faktor v rámci modelu (formula) – všimněte si, že může být aplikována i na numerickou proměnnou:

Weight ~ Height + factor(Age) + Sex

Konverze numerických hodnot do faktoru je poměrně častá zvláště u dotazníkových dat, kde čísla mohou pouze kódovat hodnoty kategoriální proměnné. Dalším případem je například vytvoření fixních efektů pro roky.

Funkce model.matrix(), kterou si estimacni funkce vola interne tedy vytvori matici planu, ktera je nasledne pouzite pri samotnem odhadu parametru modelu. Odhadova procedura si lisi podle pouzite estimacni funkce. V pripade lm() je to QR dekompozice (https://en.wikipedia.org/wiki/QR_decomposition), pri pouziti glm() jsou to napriklad ruzne numericke optimalizacni algoritmy (defaultne IWLS:https://en.wikipedia.org/wiki/Iteratively_reweighted_least_squares).

18.3.2 Výstupy estimační funkce

lm(model, data = oly12) -> est_model

class(est_model)
## [1] "lm"

Funkce lm() vrací S3 objekt třídy lm. Jiné estimační funkce vrací jiné objekty, které jsou ovšem často potomky lm. Objekt třídy lm má následující strukturu (viz ?lm):

str(est_model, max.level = 1)
## List of 13
##  $ coefficients : Named num [1:5] -1.06e+02 9.46e+01 4.10e-01 -4.09e-03 5.59
##   ..- attr(*, "names")= chr [1:5] "(Intercept)" "Height" "Age" "I(Age^2)" ...
##  $ residuals    : Named num [1:9038] -7.71 33.72 -9.15 14.68 0.11 ...
##   ..- attr(*, "names")= chr [1:9038] "1" "2" "3" "4" ...
##  $ effects      : Named num [1:9038] -6926.6 -1161.4 -96.3 -15.7 -221.1 ...
##   ..- attr(*, "names")= chr [1:9038] "(Intercept)" "Height" "Age" "I(Age^2)" ...
##  $ rank         : int 5
##  $ fitted.values: Named num [1:9038] 67.7 91.3 85.2 70.3 79.9 ...
##   ..- attr(*, "names")= chr [1:9038] "1" "2" "3" "4" ...
##  $ assign       : int [1:5] 0 1 2 3 4
##  $ qr           :List of 5
##   ..- attr(*, "class")= chr "qr"
##  $ df.residual  : int 9033
##  $ contrasts    :List of 1
##  $ xlevels      :List of 1
##  $ call         : language lm(formula = model, data = oly12)
##  $ terms        :Classes 'terms', 'formula'  language Weight ~ Height + Age + I(Age^2) + Sex
##   .. ..- attr(*, "variables")= language list(Weight, Height, Age, I(Age^2), Sex)
##   .. ..- attr(*, "factors")= int [1:5, 1:4] 0 1 0 0 0 0 0 1 0 0 ...
##   .. .. ..- attr(*, "dimnames")=List of 2
##   .. ..- attr(*, "term.labels")= chr [1:4] "Height" "Age" "I(Age^2)" "Sex"
##   .. ..- attr(*, "order")= int [1:4] 1 1 1 1
##   .. ..- attr(*, "intercept")= int 1
##   .. ..- attr(*, "response")= int 1
##   .. ..- attr(*, ".Environment")=<environment: R_GlobalEnv> 
##   .. ..- attr(*, "predvars")= language list(Weight, Height, Age, I(Age^2), Sex)
##   .. ..- attr(*, "dataClasses")= Named chr [1:5] "numeric" "numeric" "numeric" "numeric" ...
##   .. .. ..- attr(*, "names")= chr [1:5] "Weight" "Height" "Age" "I(Age^2)" ...
##  $ model        :'data.frame':   9038 obs. of  5 variables:
##   ..- attr(*, "terms")=Classes 'terms', 'formula'  language Weight ~ Height + Age + I(Age^2) + Sex
##   .. .. ..- attr(*, "variables")= language list(Weight, Height, Age, I(Age^2), Sex)
##   .. .. ..- attr(*, "factors")= int [1:5, 1:4] 0 1 0 0 0 0 0 1 0 0 ...
##   .. .. .. ..- attr(*, "dimnames")=List of 2
##   .. .. ..- attr(*, "term.labels")= chr [1:4] "Height" "Age" "I(Age^2)" "Sex"
##   .. .. ..- attr(*, "order")= int [1:4] 1 1 1 1
##   .. .. ..- attr(*, "intercept")= int 1
##   .. .. ..- attr(*, "response")= int 1
##   .. .. ..- attr(*, ".Environment")=<environment: R_GlobalEnv> 
##   .. .. ..- attr(*, "predvars")= language list(Weight, Height, Age, I(Age^2), Sex)
##   .. .. ..- attr(*, "dataClasses")= Named chr [1:5] "numeric" "numeric" "numeric" "numeric" ...
##   .. .. .. ..- attr(*, "names")= chr [1:5] "Weight" "Height" "Age" "I(Age^2)" ...
##  - attr(*, "class")= chr "lm"

Důležité jsou zejména následující položky:

  • coefficients…pojmenovaný vektor odhadnutých koeficientů
est_model$coefficients
##   (Intercept)        Height           Age      I(Age^2)          SexM 
## -1.060127e+02  9.463456e+01  4.096565e-01 -4.094392e-03  5.591553e+00
  • residuals…vektor reziduí – tj. odhadů náhodné složky \(\varepsilon\)
est_model$residuals %>% head
##          1          2          3          4          5          6 
## -7.7137568 33.7165890 -9.1502080 14.6799373  0.1103484 -1.8269273
  • fitted.values…vyrovnané hodnoty
est_model$fitted.values %>% head
##        1        2        3        4        5        6 
## 67.71376 91.28341 85.15021 70.32006 79.88965 74.82693
  • model…modifikovanou tabulku dat, která byla skutečně použita při odhadu (tj, například s vypuštěnými nepoužitými proměnnými nebo neúplnými řádky).
est_model$fitted.values %>% head
##        1        2        3        4        5        6 
## 67.71376 91.28341 85.15021 70.32006 79.88965 74.82693

Za povšimnutí stojí, že objekt obsahuje skutečně pouze odhad – data, odhadnuté koeficienty, rezidua, vyrovnané hodnoty a dodatečné informace. Neobsahuje žádné dodatečné výpočty jako například diagnostické testy.

Pro objekty třídy lm existuje metoda generické funkce print(). Její výstupy však nejsou nijak zvlášť informativní:

print(est_model)
## 
## Call:
## lm(formula = model, data = oly12)
## 
## Coefficients:
## (Intercept)       Height          Age     I(Age^2)         SexM  
##  -1.060e+02    9.463e+01    4.097e-01   -4.094e-03    5.592e+00

Obsahuje jen použité volání a odhadnuté hodnoty koeficientů. Více se dozvíme pomocí funkce summary():

summary(est_model)
## 
## Call:
## lm(formula = model, data = oly12)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -56.334  -5.717  -1.336   3.756 135.665 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -1.060e+02  2.385e+00 -44.444  < 2e-16 ***
## Height       9.463e+01  1.141e+00  82.918  < 2e-16 ***
## Age          4.097e-01  1.096e-01   3.738 0.000187 ***
## I(Age^2)    -4.094e-03  1.819e-03  -2.250 0.024442 *  
## SexM         5.592e+00  2.560e-01  21.840  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 10.13 on 9033 degrees of freedom
## Multiple R-squared:  0.6031, Adjusted R-squared:  0.6029 
## F-statistic:  3431 on 4 and 9033 DF,  p-value: < 2.2e-16

V tomto případě vidíme kromě odhadů koeficientů i směrodatné chyby a výsledky testů statistické významnosti koeficientů (v tomto případě t-testů). Výstup je také doplněn několika dalšími údaji jako je výsledek F-testu a (adjustovaný) koeficient determinace. Funkce summary() poskytuje rychlý pohled na výsledky, nicméně ten může být zavádějící. Funkce totiž vrací pouze standardní výstupy. Nijak například nereflektuje možné zkreslení odhadu směrodatných odchylek kvůli heteroskedasticitě a podobně. Všimněte si, že summary() používá méně obvyklé – a přísnější – hvězdičkové značení!

18.3.3 Práce s výsledkem odhadů

V R najdete řadu specializovaných funkcí, které dokážou z výsledného modelu získávat, nebo na jeho základě dopočítávat užitečné informace. Tabulka obsahuje jejich základní přehled:

Funkce Popis
coefficients(), coefs() Vrací odhadnuté koeficienty – obsah .$coefficients
residuals(), resid() Vrací vektor reziduí – pro objekty lm je výstup identický s .$residuals
fitted.values() Vrací očekávané hodnoty – obsah .$fitted.values
predict() Umožňuje dopočítat predikce pro jiná data, než na kterých byl model odhadnut
plot() Vrací diagnostické grafy vytvořené pomocí základní grafiky (ne v ggplot2)
confint() Vrací konfidenční intervaly pro odhady koeficientů
deviance() Vrací MSE – průměr čtverců reziduí
vcov() Vrací odhad kovarianční matice
logLik() Vrací log-likelihood
AIC() Vrací Akaikovo informační krítérium (AIC)
BIC() Vrací Schwarzovo Bayesian kritérium (BIC)
nobs() Vrací počet pozorování

Pro některé účely je vhodné seznámit se i se sofistikovanějšími funkcemi. Pro účely diagnostiky nebo okometrického posouzení kvality vyrovnání může být užitečné výsledky odhadu vizualizovat. Výsledky jsou však schované ve zvláštním objektu a ne v tabulce, kterou potřebujeme pro použití s ggplot2. Pro transformaci různých objektů do tabulky existuje v ggplot2 funkce fortify(). Stejnou funkcionalitu poskytuje i balík broom. Pro objekty třídy lm je ekvivalentem funkce broom::augment():

library(broom)
augment(est_model) %>% as_tibble %>% print(n = 5)
## # A tibble: 9,038 x 12
##   Weight Height   Age I.Age.2. Sex   .fitted .se.fit .resid    .hat .sigma
##    <int>  <dbl> <int> <I<dbl>> <chr>   <dbl>   <dbl>  <dbl>   <dbl>  <dbl>
## 1     60   1.7     23      529 M        67.7   0.216 -7.71  4.53e-4   10.1
## 2    125   1.93    33     1089 M        91.3   0.221 33.7   4.74e-4   10.1
## 3     76   1.87    30      900 M        85.2   0.175 -9.15  2.99e-4   10.1
## 4     85   1.78    26      676 F        70.3   0.186 14.7   3.36e-4   10.1
## 5     80   1.82    27      729 M        79.9   0.155  0.110 2.35e-4   10.1
## # … with 9,033 more rows, and 2 more variables: .cooksd <dbl>, .std.resid <dbl>

Pozor, broom navrací tibble. Proto je užitečné výstup do tibble konvertovat. Výsledek je již jednoduše použitelný pro vizualizaci pomocí ggplot2. Následující obrázek ukazuje korelaci pozorovaných (observed) a vyrovnaných (fitted) hodnot. Do obrázku je přidána pomocí geom_abline() i osa kvadrantu na která se pozorované a vyrovnané hodnoty rovnají.

est_model %>% 
  augment() %>% 
  ggplot(
    aes(x = Weight, y = .fitted)
  ) +
  geom_point(alpha = 0.05) +
  geom_abline(slope = 1, intercept = 0, color = "red") +
  scale_x_continuous(name = "Observed values") +
  scale_y_continuous(name = "Fitted values")

Balík broom obsahuje i další užitečné funkce: tidy() a glance(). Funkce tidy() vrací tabulku s odhady parametrů, směrodatných odchylek, testových statistik a p-hodnot:

tidy(est_model)
## # A tibble: 5 x 5
##   term          estimate std.error statistic   p.value
##   <chr>            <dbl>     <dbl>     <dbl>     <dbl>
## 1 (Intercept) -106.        2.39       -44.4  0.       
## 2 Height        94.6       1.14        82.9  0.       
## 3 Age            0.410     0.110        3.74 1.87e-  4
## 4 I(Age^2)      -0.00409   0.00182     -2.25 2.44e-  2
## 5 SexM           5.59      0.256       21.8  4.38e-103

Funkce glance() vrací opět tabulku. Jejím obsahem ovšem nejsou údaje týkající se jednotlivých proměnných, ale modelu jako celku:

glance(est_model)
## # A tibble: 1 x 11
##   r.squared adj.r.squared sigma statistic p.value    df  logLik    AIC    BIC
##       <dbl>         <dbl> <dbl>     <dbl>   <dbl> <int>   <dbl>  <dbl>  <dbl>
## 1     0.603         0.603  10.1     3431.       0     5 -33746. 67504. 67546.
## # … with 2 more variables: deviance <dbl>, df.residual <int>

Tyto funkce jsou mimořádně užitečné při strojovém zpracovávání velkého množství odhadnutých modelů. Funkce z balíku broom přitom neslouží jenom pro převádění objektů lm do tabulky. Jejich záběr je mnohem obecnější a obsahují metody pro mnohem více tříd objektů.

Zvláštní pozornost se vyplatí věnovat funkci predict(). Ty v základní konfiguraci vrací prostě vyrovnané hodnoty:

all.equal(predict(est_model),fitted(est_model))
## [1] TRUE

Při mnoha aplikacích nás spíše zajímá schopnost modelu predikovat out-of-sample. Tedy predikovat hodnoty vysvětlované proměnné na jiném vzorku dat, než který byl použit k odhadu parametrů. I pro tento účel se hodí funkce predict().

Nejprve si tabulku oly12 rozdělíme na dvě dílčí tabulky oly12_a a oly12_b:

idx <- sample(nrow(oly12), round(nrow(oly12)/2))

oly12[idx,]  -> oly12_a
oly12[-idx,]  -> oly12_b

Pro odhad parametrů použijeme tabulku oly12_a:

oly12_a %>% 
    lm(model, data=.) -> est_model_a

Na základě odhadnutého modelu vypočítáme očekávané hodnoty Weight pro pozorování ze vzorku oly12_b:

predict(est_model_a, newdata = oly12_b) -> prediction_oly12_b

Výsledkem je vektor predikovaných hodnot. Podívejme se, jak si model vedl při predikci out-of-sample:

oly12_b %>%
    bind_cols(.fitted = prediction_oly12_b) %>% 
    mutate(
        sample = "B"
    ) -> oly12_b

est_model_a %>% 
  augment() %>% 
  mutate(
    sample = "A"
  ) %>% 
  bind_rows(oly12_b) %>% 
     ggplot(
        aes(
            x = Weight,
            y = .fitted
        )
    ) +
    geom_point(
        alpha = 0.1
    ) +
  geom_abline(slope = 1, intercept = 0, color = "red") +
  facet_wrap("sample", labeller = as_labeller(
    c("A"="In-sample predictions","B"="Out-of-sample predictions")
    ))

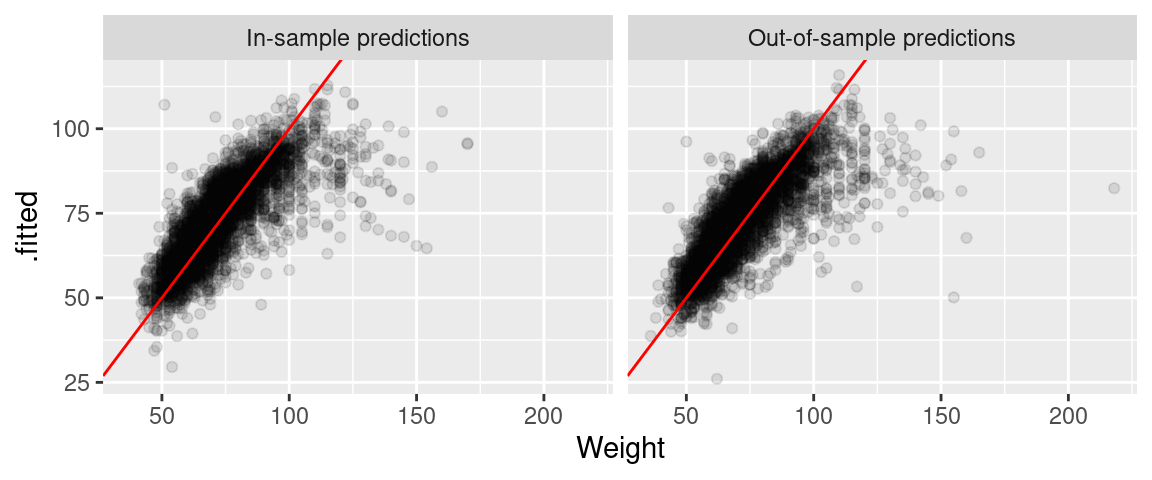
Obrázky zhruba ukazují, že odhadnutý model si vede dobře i v out-of-sample predikcích. tedy predikcích vypočítaných na jiných datech, než jaké byly použity pro odhad modelu. Vzhledem k tomu, že vzorek byl rozdělen náhodně to asi není žádné velké překvapení.

18.3.4 Další estimační funkce a kde je najít

Následující tabulka představuje pár estimačních funkcí dostupných v R.

Model/estimátor Funkce Poznámka
Logit/probit glm() Modely diskrétní volby
Poisson glm() Count data
Poisson pseudo-ML (PPML) glm() Např. gravitační modely
Lineární panelová data plm::plm() pooled, FE, RE,…
Arellano-Bond plm::pgmmm() Dynamické panely
Common Correlated Effects plm::pcce() Např. gravitační modely
Poisson, logit, ordered probit,… (na panelu) pglm::pglm()
Tobit AER::tobit()
2SLS AER::ivreg()
Heckit (Tobit 2) sampleSelection::heckit()

…a mnoho, mnoho dalších.