18.2 Specifikace modelu pomocí formula

Fungování ekonometrických nástrojů můžeme ilustrovat na příkladu datasetu s výškou, váhou, věkem, sportem, a pohlavím sportovců, kteří se zúčastnili olympijských her v Londýně v roce 2012 (dostupný v VGAMdata::oly12):

VGAMdata::oly12 %>% 
  mutate(
    Sport = str_extract(Sport, "[:alnum:]*")
  ) %>% 
  select(
    Height, Weight, Sex, Age, Sport
  ) %>% 
  as_tibble %>%
  drop_na() %>% 
  mutate_if(is.factor,as.character) -> oly12

print(oly12, n=5)

## # A tibble: 9,038 x 5
##   Height Weight Sex     Age Sport    
##    <dbl>  <int> <chr> <int> <chr>    
## 1   1.7      60 M        23 Judo     
## 2   1.93    125 M        33 Athletics
## 3   1.87     76 M        30 Athletics
## 4   1.78     85 F        26 Athletics
## 5   1.82     80 M        27 Handball 
## # … with 9,033 more rows

Nejprve nás bude zajímat vztah mezi váhou a výškou sportovců. Ten si můžeme vykreslit pomocí jednoduchého bodového grafu:

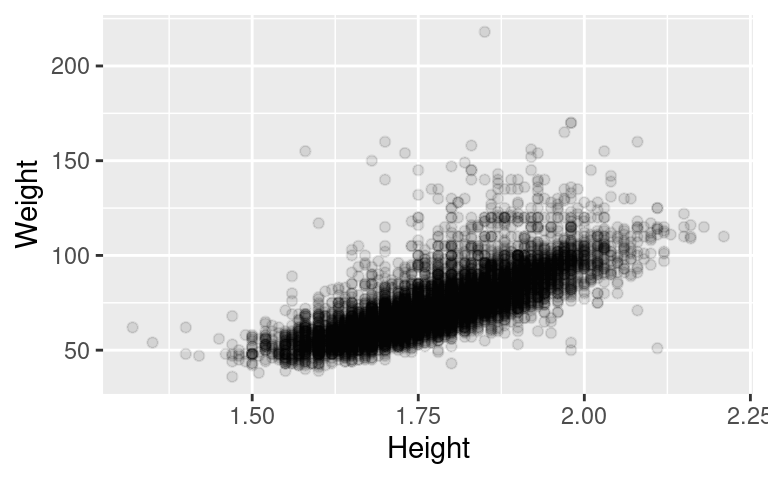
Zdá se, že existuje lineární vztah mezi váhou a výškou sportovců, který můžeme popsat rovnicí: \[Weight = \alpha + \beta Height + \varepsilon\] kde \(\alpha\) a \(\beta\) jsou neznámé parametry, které chceme odhadnout a \(\varepsilon\) je náhodná složka.

Tuto rovnici si můžeme představit jako přímku, která je proložena mrakem pozorování:

## `geom_smooth()` using formula 'y ~ x'

Rovnici však musíme zapsat tak, aby byla srozumitelná i pro R. K tomu slouží objekty třídy formula. Jejich formulace následuje syntax:

LHS ~ RHS

Tedy výrazy na levé straně (LHS) \(=\) (zastoupené znakem ~) výrazy na pravé straně (RHS). Rovnici vysvětlující váhu bychom tedy mohli popsat jako:

model <- Weight ~ Height
class(model)

## [1] "formula"

V ekonomii je závislá (vysvětlovaná) proměnná (tedy proměnná na levé straně rovnice) funkcí více než jedné nezávislé (vysvětlující) proměnné. Pokud bychom chtěli vysvětlovat váhu nejen výškou, ale i věkem, potom bychom rozšířili specifikaci následujícím způsobem:

model <- Weight ~ Height + Age

Dodatečná proměnné jsou přidávány pomocí +.

Za povšimnutí stojí, že při použití takovéto specifikace by byl model odhadnut s úrovňovou konstantou \(\alpha\) – i když není explicitně v rovnici přítomna. Explicitně se naopak musí zadat její nepřítomnost připojením -1 nebo 0:

model <- Weight ~ Height - 1
model <- Weight ~ Height + 0

Jména proměnných v rovnici musí odpovídat jménům sloupců v datové tabulce. Zásadní výhodou R je, že do rovnice je možné zadat i transformace dat:

model <- Weight ~ log(Height)
model <- Weight ~ Height >= 1.8

První varianta například odpovídá specifikaci:

\[Weight = \alpha + \beta \log(Height) + \varepsilon\]

Ve druhé je váha vysvětlována dummy (umělou proměnnou). Výraz Height >= 1.8 vytvoří logickou proměnnou, která je při volání estimační funkce transformována na vektor s hodnotami 1 a 0.

Není tedy potřeba vytvářet nové transformované sloupce v datové tabulce. To je velký rozdíl mezi R a Statou, Gretlem,… (Jakkoliv je v některých případech vytvoření transformovaných proměnných do tabulky doporučeníhodné.)

V rovnici může být přímo přítomna celá řada funkcí – s výjimkou těch, jejichž interpretace by nebyla jasná. Pokud bychom například chtěli odhadnout modelovou specifikaci

\[Weight = \alpha + \beta (Height + Age) + \varepsilon\]

potom je nutná sdělit R, že má nejdříve sečíst Height a Age a pro vysvětlení Weight použít až výsledný součet. Pro tyto účely se používá funkce I(). Ta sděluje, že se mají nejprve provést operace definované uvnitř funkce a pro odhad použít až výsledek.

Výše uvedený příklad by se tak R tlumočil jako

model <- Weight ~ I(Height + Age)

Třída formula umožňuje jednoduše jednoduše definovat i interakční členy pomocí operátorů dvojtečka (:) a hvězdička (*):

model <- Weight ~ Height:Sex

Chápe R jako

\[Weight = \alpha + \beta Height\times Sex_{male} + \gamma Height\times Sex_{female} + \varepsilon\] Tato rovnice vyjadřuje možný odlišný mezní efekt výšky na váhu u mužů a žen. Výsledné proložení mrakem pozorování by se tak v bodovém grafu výše vlastně rozpadlo na dvě přímky s odlišným sklonem (parametry \(\beta\) a \(\gamma\)) a shodnou úrovňovou konstantou \(\alpha\).

Další možností jak popsat interakci proměnných je *:

model <- Weight ~ Height*Sex

Tato formula odpovídá jiné rovnici:

\[Weight = \alpha + \beta Height + \epsilon Sex_{male} + \gamma Height\times Sex_{male} + \varepsilon\] Tato specifikace umožňuje odlišnost regresní křivky pro muže a ženy jak ve sklonu, tak v úrovňové konstantě.

Zvláštní význam má i symbol stříšky (^). Rovnici

\[Weight = \alpha + \beta_1 Height + \beta_2 Age + \beta_3 Sex_{male} + \gamma_1 Height\times Sex_{male} + \gamma_2 Height\times Age + \gamma_3 Sex_{male}\times Age + \varepsilon\] můžeme zapsat jako:

model <- Weight ~ (Height + Age + Sex)^2

Výraz se přeloží tak, že výsledná rovnice obsahuje jednotlivé proměnné a také jejich interakce do, v tomto případě, druhého řádu.

Pro třídu formula jsou implementovány i některé zajímavé metody. Velmi užitečná je například funkce update() s velmi prostou syntaxí:

update(old,new,...)

Kde old je původní rovnice a new pravidla, která stanovují, jak se původní rovnice má upravit.

model <- Weight ~ Height + Age
print(model)

## Weight ~ Height + Age

Takto můžeme zachovat všechny proměnné – reprezentované pomocí . a jen některou přidat nebo odebrat:

model %>% 
  update(. ~ . -Age)

## Weight ~ Height

Nebo je možné nahradit celou stranu rovnice:

model %>% 
  update(. ~ Age)

## Weight ~ Age