18.4 Diagnostika
18.4.1 Vlivná pozorování
Populárním způsobem, jak najít pozorování, která významně ovlivňují výsledky modelu, je použití leave-one-out strategií. V nich se sleduje efekt vyloučení jednoho pozorování na odhady koeficientů, popřípadě na vyrovnaná pozorování. V R jsou implementovány v influence.measures():
influence.measures(est_model) -> infl_obs
infl_obs %>% class## [1] "infl"influence.measures() najednou volá celou řadu diagnostických testů – mj. dfbetas() (vliv jednoho pozorování na odhadnuté koeficienty) a dffits() (vliv jednoho pozorování na vyrovnané hodnoty).
Výstupní objekt třídy infl obsahuje dva prvky (matice). .$infmat obsahuje hodnoty jednotlivých statistik a .$is.inf rozhodnutí (o podezření), zda se jedná o vlivné pozorování.
Viz obrázek:
augment(est_model) %>%
bind_cols(.,as.data.frame(infl_obs$is.inf)) %>%
ggplot(
aes(x=Weight,
y=.fitted)
) +
geom_point(
aes(
color = dffit
),
alpha = 0.2
) +
xlab("Observed values") +
ylab("Fitted values") +
scale_color_discrete(name="Influential\nobservation\n(DFFIT)")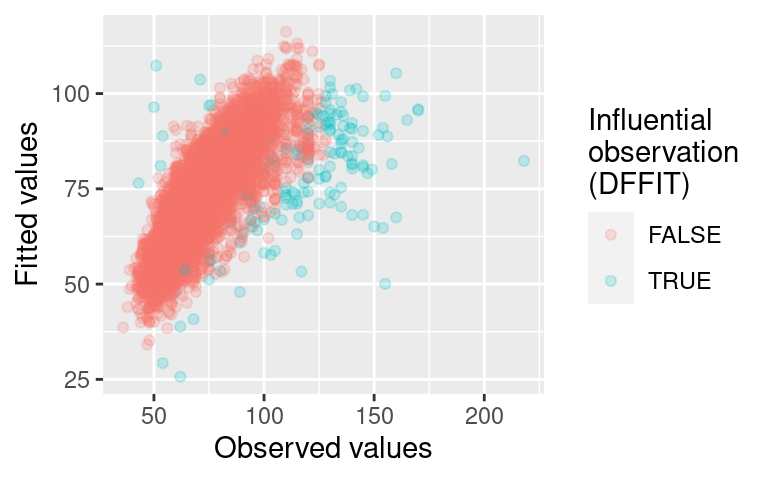
Hodnoty, u kterých se predikce velmi odlišuje od pozorovaných hodnot jsou podle statistiky DFFIT jsou navrženy jako vlivné.
Tyto výsledky naznačují, že se v datech může dít něco zvláštního, nebo že nemáme k dispozici dostatečný počet pozorování z určité části prostoru – v tomto případě například u sportovců s vyšší hmotností.
18.4.2 Normalita reziduí
Prvním způsobem, jak ověřit normalitu reziduí je pohledem na jejich rozdělení. Pomoci může například Q-Q plot, který porovnává kvantily normálního rozdělení a standardizovaných reziduí. V případě, že je rozdělení reziduí normální, by pozorování měla ležet na ose kvadrantu:
augment(est_model) %>%
ggplot(
aes(sample = .std.resid)
) +
geom_qq() +
geom_abline(
slope = 1,
intercept = 0,
color = "red"
)
Ani jeden okometrický test pro normalitu příliš nehovoří. Nicméně je potřeba nepodlehnout zdání. R poskytuje v balíku normtest celou baterii statistických testů.
Například můžeme zkusit otestovat normalitu pomocí Jarque-Bera testu:
library(normtest)
residuals(est_model) %>%
jb.norm.test() -> jb
class(jb)## [1] "htest"print(jb)##
## Jarque-Bera test for normality
##
## data: .
## JB = 82199, p-value < 2.2e-16Výstupem jb.norm.test() je objekt typu htest. Tato třída je oblíbená pro výsledky statistických testů. Pro tuto třídu existují metody v balíku broom, např.:
tidy(jb)## # A tibble: 1 × 3
## statistic p.value method
## <dbl> <dbl> <chr>
## 1 82199. 0 Jarque-Bera test for normalityNulovou hypotézou Jarque-Bera testu je normalita, kterou tento test zamítá.
18.4.3 Testy linearity
Z testů linearity je dostupný například Rainbow test, který srovnává kvalitu vyrovnání v modelech odhadnutých “uprostřed” pozorování a na celém vzorku.
V R je Rainbow test dostupný v balíku lmtest ve funkci raintest:
raintest(formula, fraction = 0.5, order.by = NULL, center = NULL,
data=list())Parametr fraction udává velikost samplu pro odhad modelu “uprostřed.” V parametru order.by se udává proměnná, podél které se mají pozorování řadit.
Parametr formula může být naplněn i odhadnutým lm modelem. V tom případě není nutné zabývat se parametrem data.
library(lmtest)
raintest(model, order.by = ~ Height, data = oly12)##
## Rainbow test
##
## data: model
## Rain = 1.1287, df1 = 4519, df2 = 4514, p-value = 2.397e-05Rain test v tomto případě zamítá nulovou hypotézu. To znamená, že fit na neomezeném vzorku je významně horší, než na podmnožině “prostředních” pozorování. Tento výsledek indikuje možný problém s linearitou.
18.4.4 Heteroskedasticita a odhad robustních chyb
Pokud je porušena homoskedasticita – tzn. konstantní rozptyl náhodné složky – potom není OLS estimátor BLUE (Best linear unbiased estimator), nicméně odhady parametrů jsou stále nevychýlené (unbiased). To bohužel neplatí pro odhady jejich rozptylu – ty naopak vychýlené jsou a v důsledku jsou nedůvěryhodné i testy statistické významnosti parametrů.
est_model %>%
augment() %>%
arrange(Height) %>%
ggplot(
aes(
x = Height,
y = .resid
)
) +
geom_point(
alpha = 0.1
) +
ylab("Residuals")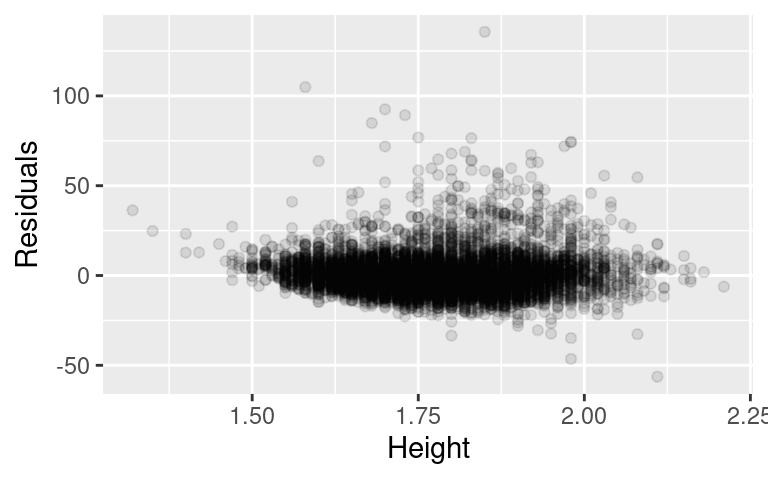
V reálném světě je podmínka homoskedasticity porušena velmi často. Jestli tomu tak je můžeme testovat pomocí mnoha testů. Jako příklad mohou sloužit příbuzné testy bptest() z balíku lmtest a ncvTest z balíku car:
lmtest::bptest(est_model)##
## studentized Breusch-Pagan test
##
## data: est_model
## BP = 73.288, df = 4, p-value = 4.585e-15car::ncvTest(est_model)## Non-constant Variance Score Test
## Variance formula: ~ fitted.values
## Chisquare = 535.0632, Df = 1, p = < 2.22e-16Oba testy testují nulovou hypotézu o homoskedasticitě oba ji suverénně zamítají – p-hodnoty obou testů jsou v podstatě nerozlišitelné od nuly.
Odhady směrodatných chyb lze korigovat použitím tzv. HC (heteroskedasticity consistent) estimátorů kovarianční matice. Ty jsou implementovány například v balících car (car::hccm), ale zejména v balíku sandwich.
Balík sandwich obsahuje celou řadu nástrojů pro odhad kovarianční matice pro průřezová i panelová data. Bližší pozornost budeme věnovat dvěma. Základní funkci vcovHC() a také relativně nově implementované funkci pro výpočet klastrovaných robustních chyb vcovCL().
Obě dvě funkce mají podobnou syntax:
vcovHC(x,
type = c("HC3", "const", "HC", "HC0", "HC1", "HC2", "HC4", "HC4m", "HC5"),
omega = NULL, sandwich = TRUE, ...)vcovCL(x, cluster = NULL, type = NULL, sandwich = TRUE, fix = FALSE, ...) Vstupem funkce je odhadnutý model (x). V parametru type se potom specifikuje způsob korekce heteroskedasticity (viz ?vcovHC()). V případě funkce vcovCL() je navíc nutné specifikovat proměnnou, nebo v případě více dimenzí proměnné, podle kterých se mají standardní chyby klastrovat. Klastrování se typicky používá v situaci, kdy určitá pozorování na sobě nejsou nezávislá. Klasický příklad je prospěch dětí z jedné třídy. Podstata dat sportovců naznačuje, že i v tomto případě je klastrování namístě. Jako specifické skupiny můžeme chápat sportovce věnující se jedné disciplině. Po vcovCL() tedy bude chtít spočítat kovarianční maticí klastrovanou podél proměnné Sport. Tu musíme dodat jako samostatný vektor. V objektu totiž není zahrnuta:
library(sandwich)
vcovCL(est_model, cluster = oly12$Sport)## (Intercept) Height Age I(Age^2) SexM
## (Intercept) 144.744530958 -87.73269188 0.544857828 -7.405519e-03 9.080987791
## Height -87.732691881 57.87470724 -0.914600493 1.437195e-02 -6.275686441
## Age 0.544857828 -0.91460049 0.079432487 -1.394717e-03 0.137949915
## I(Age^2) -0.007405519 0.01437195 -0.001394717 2.566568e-05 -0.002251259
## SexM 9.080987791 -6.27568644 0.137949915 -2.251259e-03 0.979011051Výsledkem je odhad kovarianční matice. Zpravidla nás ovšem více zajímá odhad významnosti parametrů – provedení statistických testů s použitím robustní kovarianční matice jako vstupu. Pro tento účel použijeme funkci coeftest() z balíku lmtest:
coeftest(x, vcov. = NULL, df = NULL, ...)Prvním vstupem funkce coeftest() je odhadnutý model. (Funkce má implementovány metody pro modely třídy lm a glm.) Druhým parametrem je kovarianční matice nebo funkce, která se má použít pro její výpočet. Pokud je tento parametr ponechán prázdný, potom coeftest() použije nekorigovanou kovarianční matici:
library(lmtest)
coeftest(est_model)##
## t test of coefficients:
##
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -1.0601e+02 2.3853e+00 -44.4438 < 2.2e-16 ***
## Height 9.4635e+01 1.1413e+00 82.9183 < 2.2e-16 ***
## Age 4.0966e-01 1.0960e-01 3.7378 0.0001868 ***
## I(Age^2) -4.0944e-03 1.8193e-03 -2.2505 0.0244416 *
## SexM 5.5916e+00 2.5603e-01 21.8397 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Zadaní jména funkce jako parametru vcov. je vhodné tehdy, pokud nepotřebujete provádět žádné další nastavení parametrů výpočtu kovarianční matice:
coeftest(est_model, vcov. = vcovHC)##
## t test of coefficients:
##
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -1.0601e+02 2.4526e+00 -43.2250 < 2.2e-16 ***
## Height 9.4635e+01 1.2120e+00 78.0841 < 2.2e-16 ***
## Age 4.0966e-01 9.2268e-02 4.4398 9.109e-06 ***
## I(Age^2) -4.0944e-03 1.5164e-03 -2.7002 0.006944 **
## SexM 5.5916e+00 2.4404e-01 22.9123 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1V případě klastrovaných chyb však potřebuje takové nastavení provést – minimálně potřebujeme zadat vektor podél kterého se má klastrovat. Do vcov. v tomto případě potřebujeme zadat celou kovarianční matici – tedy výstup funkce vcovCL:
coeftest(est_model, vcov. = vcovCL(est_model, cluster = oly12$Sport))##
## t test of coefficients:
##
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -1.0601e+02 1.2031e+01 -8.8116 < 2.2e-16 ***
## Height 9.4635e+01 7.6075e+00 12.4396 < 2.2e-16 ***
## Age 4.0966e-01 2.8184e-01 1.4535 0.1461
## I(Age^2) -4.0944e-03 5.0661e-03 -0.8082 0.4190
## SexM 5.5916e+00 9.8945e-01 5.6512 1.642e-08 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Klastrovat lze podél více proměnných. V tomto případě je potřeba do parametru cluster vložit list vektorů nebo data.frame. Nyní zkusíme cvičně klastrovat nejen podle sportovního odvětví, ale i podle pohlaví:
coeftest(est_model, vcov. = vcovCL(est_model, cluster = list(oly12$Sport, oly12$Sex)))##
## t test of coefficients:
##
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -1.0601e+02 2.6150e+01 -4.0540 5.076e-05 ***
## Height 9.4635e+01 1.2569e+01 7.5295 5.584e-14 ***
## Age 4.0966e-01 3.3167e-01 1.2351 0.2168
## I(Age^2) -4.0944e-03 4.2600e-03 -0.9611 0.3365
## SexM 5.5916e+00 1.1367e+00 4.9189 8.857e-07 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Výstupem funkce coeftest() je objekt speciální třídy coeftest. Pokud ho chceme převést na tabulku můžeme použít funkci broom::tidy():
coeftest(est_model, vcov. = vcovCL(est_model, cluster = list(oly12$Sport, oly12$Sex))) %>% tidy()## # A tibble: 5 × 5
## term estimate std.error statistic p.value
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 (Intercept) -106. 26.1 -4.05 5.08e- 5
## 2 Height 94.6 12.6 7.53 5.58e-14
## 3 Age 0.410 0.332 1.24 2.17e- 1
## 4 I(Age^2) -0.00409 0.00426 -0.961 3.37e- 1
## 5 SexM 5.59 1.14 4.92 8.86e- 718.4.5 Dignostika graficky
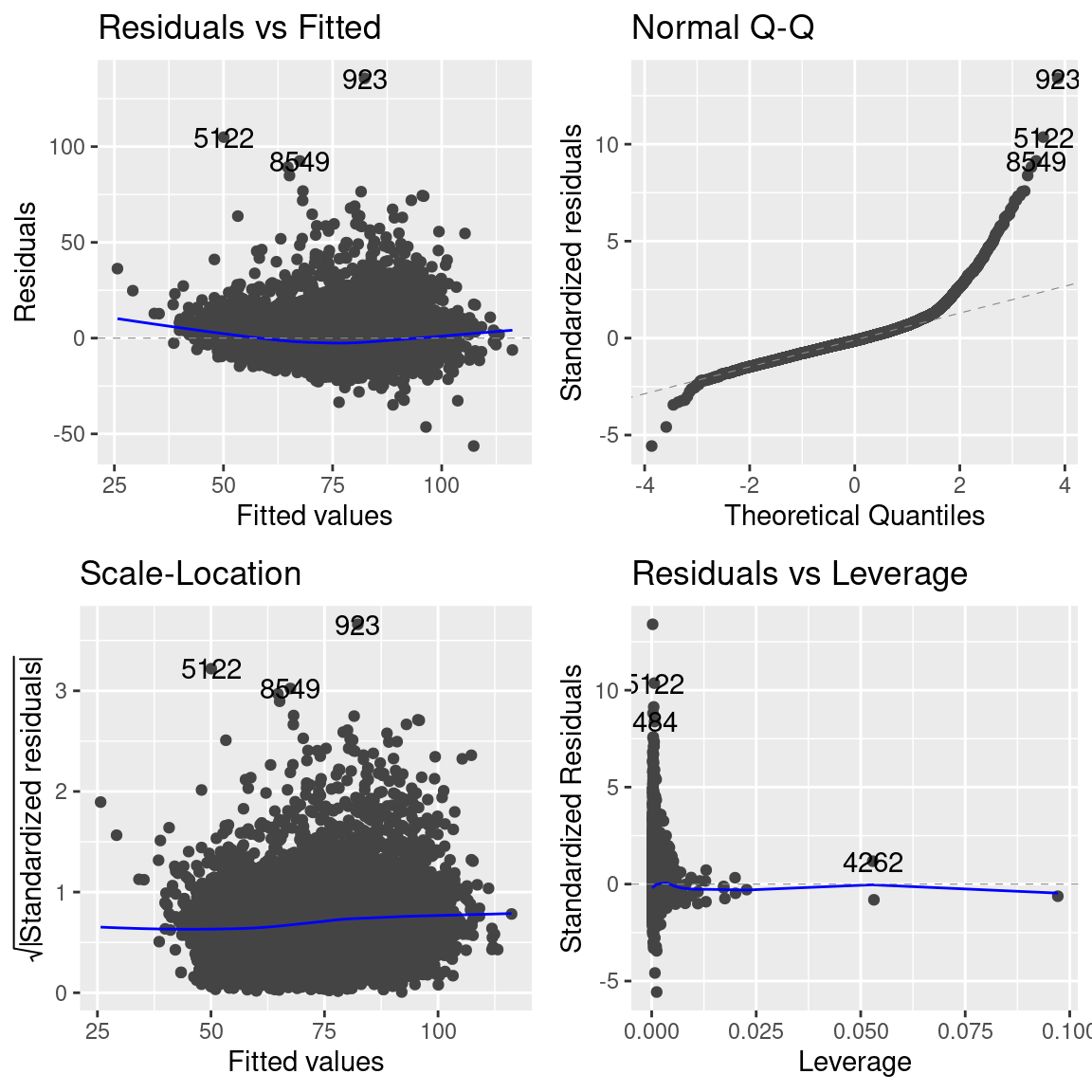
V mnoha případech je užitečné se na diagnostiku podívat prostřednictvím vizualizací. Tuto možnost nabízí například funkce plot(), která má pro tento účel implementovanou metodu. Její fungování můžete vyzkoušet zadáním plot(est_model). Tento postup logicky pracuje se základní grafikou. Existují však i řešení, které podobně uživatelsky přítulně vykreslí diagnostické grafy s pomocí ggplot2. Jedním z nich je funkce ggplot2::autoplot(), která využívá služeb balíku ggfortify:
library(ggfortify)
autoplot(est_model)