17.5 Statistické transformace
ggplot2 umožňuje nejen vykreslovat samotná data, ale i jejich interně vytvořené statistické transformace. Příkladem může být například proložení křivkou (geom_smooth()). Jejich tvorbu mají na starosti funkce stat_*(). Vztah mezi funkcemi geom_*() a stat_*() není úplně jasný. Každá transformace (stat) má svůj výchozí (přednastavený) geometrický tvar (geom) a každý geom má svůj výchozí stat. V některých případech tak může být jedno, jestli uživatel volá geom nebo ekvivalentní stat, Viz například použití stat_smooth():
diamonds %>%
ggplot(
aes(x = carat, y = price)
) +
geom_point() +
stat_smooth()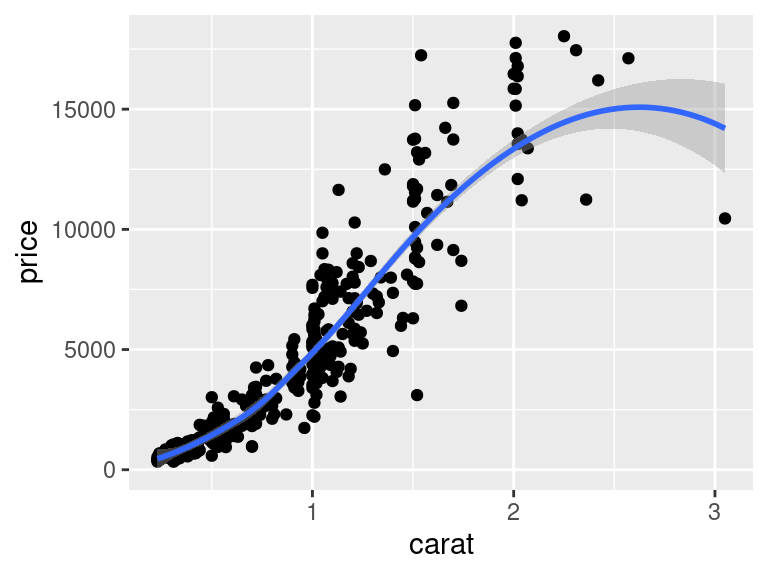
Tato nejednoznačnost vymezení toho, co vlastně dělá stat_*() a co geom_*() je velmi otravnou nedokonalostí v návrhu ggplot2 (a v ggvis je již vyřešena). Pokud není nevyhnutelné volat přímo stat_*() nutné, je lepší vždy používat funkce geom_*().
Pro přímé volání stat_*() existovaly v podstatě dva důvody:
- potřeba specifických nastavení statistických transformací
- potřeba použití jiného než standardního geomu pro vykreslení statistické transformace
Pohledem do nápovědy zjistíte, že stat_smooth() umožňuje mnohem více nastavení vyhlazování:
geom_smooth(mapping = NULL, data = NULL, stat = "smooth",
position = "identity", ..., method = "auto", formula = y ~ x,
se = TRUE, na.rm = FALSE, show.legend = NA, inherit.aes = TRUE)
stat_smooth(mapping = NULL, data = NULL, geom = "smooth",
position = "identity", ..., method = "auto", formula = y ~ x,
se = TRUE, n = 80, span = 0.75, fullrange = FALSE, level = 0.95,
method.args = list(), na.rm = FALSE, show.legend = NA,
inherit.aes = TRUE)V novějších verzích ggplot2 se však již dají zpravidla předávat hodnoty parametrů pro stat_*() prostřednictvím ... v geom_*(). Tato možnost prakticky eliminuje potřebu volat stat_*() funkce přímo kvůli nastavení statistických transformací.
Druhý důvod pro přímé použití stat_*() funkce však stále trvá. V některých případech můžete potřebovat použít pro vyreslení transformace netypický geom. Příkladem může být například zobrazování jádrové hustoty rozdělení dvou proměnných nikoliv pomocí vrstevnic (standardní zobrazení), ale pomocí barevných polygonů. (Výsledkem by byly například barevné plochy s barvou sytější tam, kde je odhadnuta vyšší hustota.) Tyto úlohy jsou však bezpochyby z kapitoly pro pokročilé.