P000 Architektura počítačů
Obsah
|
Pojmy
Technické vybavení počítače -
Hardware - HW - souhrnný název pro veškerá
fyzická zřízení, kterými je počítač vybaven.
Programové vybavení počítače -
Software - SW
Firmware - programy
tvořící součást technického vybavení počítače.
1 bit ( z anglického BInary
digiT) 1b - základní jednotka informace.
1 slabika = 1byte 1B -
skupina 8 bitů.
1 slovo = 1word - několik
(2, 4, 6, 8) slabik.
Paměť (Memory) -
zařízení pro uchovávání informace (konkrétně
binárně kódovaných dat).
Adresa v paměti -
číselné označení místa v paměti.
Nejmenší adresovatelná jednotka
- kapacita místa v paměti, které má vlastní adresu
(slabika, slovo).
Kapacita paměti
1KB = 210 slabik = 1.024 slabik
1MB = 220 slabik = 1.048.576
slabik
1GB = 230 slabik = 1.073.741.824
slabik
1 TB
RAM - paměť pro čtení i
zápis
ROM - paměť pouze pro
čtení
Paměť s přímým přístupem
Paměť se sekvenčním přístupem
Vnitřní (operační) paměť
Vnější (periferní) paměť
Registr
V / V zařízení (I / O
Equipment)
Řadič (Controler) -
zařízení převádějící příkazy v symbolické formě
(instrukce) na posloupnost signálů ovládajících
připojené zařízení.
Nastudovat:
Historie počítačů
Novodobá historie počítačů se datuje od
roku 1938, kdy německý stavební inženýr Konrád Zuse
sestrojil první mechanický počítač Z1. Pozdější model
Z3 měl 2600 telefonních relátek a byl programovatelný.
Dříve již v roce 1801 řídí Francouz Maria Jacquard
tkalcovský stav pomocí děrné pásky a v roce 1833
vyvíjí Angličan Charles Babage tzv."Analytical
Engine" pracující s děrnými štítky. Na svou dobu
vlastně příliš komplikovaný stroj. Počítač ENIAC
(Electronic Numerical Integrator and Computer) sestrojený
v r. 1946 na University of Pennsylvania byl prvním
všeobecně použitelným počítačem na světě. Vážil 30
tun, zabíral 15 m2 a měl příkon 174kW pro
17460 elektronek, 1500 relé, 70000 odporů a 10000
kondenzátorů. Pracoval na frekvenci 100 kHz a pro
násobení potřeboval 2,8 mikrosekundy. Stroj nepracoval binárně,
nýbrž dekadicky. Paměť obsahovala 20 střádačů,
každý měl kapacitu 10 dekadických číslic. Každá
číslice byla uložena uvnitř kruhu 10 elektronek, z nichž
v jednom okamžiku mohla právě jedna reprezentovat
"jedničku". Stroj se programoval ručně pomocí
přepínačů a kabelových kontaktů. Byl chlazen vzduchem
hnaným vrtulemi dvou leteckých motorů. V roce 1955 byl
rozebrán. Ideu řízení počítače programem publikoval
v roce 1945 pan John von Neumann. Další vývoj v oblasti
počítačů byl velmi prudký. Byl uveden do provozu
počítač IAS (1952), který se stal vzorem pro první
velkosériově vyráběný počítač IBM 701.
V Československu byl uveden do provozu první reléový
počítač SAPO už v roce 1958. V roce 1948 byl poprvé
předveden tranzistor; komerčně byl využit teprve v roce
1952. Integrovaný obvod s více tranzistory byl vyroben
koncem 50.let. Složitost integrovaných obvodů se hodnotí
podle počtu logických členů (hradel) realizovaných na
jedné křemíkové základně.
Generace počítačů
Pokusíme-li se charakterizovat vývoj počítačů,
můžeme pro zařazení do generací použít několik rysů.
Nejvhodnější bude asi seřazení podle použitých
součástek. Shrňme si jej v tabulce na obrázku.
Počítače 5. generace jsou charakterizovány kvalitativně
odlišnými prostředky komunikace s uživatelem, operační
rychlostí a prvky umělé inteligence.
| Generace |
Rok |
Použité součástky |
| 0. |
1940 |
relé |
| 1. |
1950 |
elektronky |
| 2. |
1958 |
tranzistory |
| 3. |
1964 |
integrované obvody |
| 3.,5. |
1972 |
LSI |
| 4. |
1981 |
VLSI |
Kategorie
počítačů
Další typ klasifikace počítačů vychází z výkonu
počítačů a z jejich aplikačního nasazení. Definujme si
tyto čtyři kategorie počítačů:
mikropočítače
minipočítače
střediskové počítače
superpočítače
Všechny tyto kategorie existují v jednom čase (současné
době) vedle sebe. Mikropočítače jsou určeny pro
každodenní používání jednomu uživateli. Někdy se tato
kategorie nazývá také "osobní počítače".
Mikropočítače existují díky mikroprocesorům, jejichž
nízká cena dovoluje široké použití. Minipočítač
sdílí většinou více uživatelů prostřednictvím více
terminálů, nebo slouží jako komunikační uzel
počítačové sítě apod. Střediskový počítač
(Mainframe) svým vysokým výkonem slouží
k vědeckotechnickým výpočtům a velkým počtem V/V
zařízení pro zpracovávání hromadných dat. Typickými
aplikacemi superpočítačů jsou vojenství, meteorologie,
seismologie, naftový průmysl, atomová fyzika apod.
Koncepce Johna von Neumanna
V roce 1946 pan John von Neumann a jeho kolegové
z Princeton Institute for Advanced Studies vyprojektovali
nový počítač postavený na těchto pravidlech:
- Počítač obsahuje operační paměť, ALJ, řadič,
V/V zařízení.
- Předpis pro řešení úlohy je převeden do
posloupnosti instrukcí.
- Údaje a instrukce jsou vyjádřeny binárně.
- Údaje a instrukce se uchovávají v paměti na
místech označených adresami.
- Ke změně pořadí provádění instrukcí se
používají instrukce podmíněného a
nepodmíněného skoku.
- Programem řízené zpracování dat probíhá
v počítači samočinně.
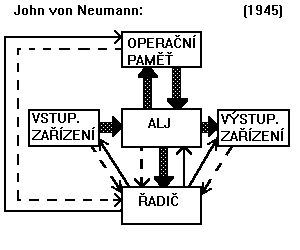
Struktura von Neumannova IAS počítače je
na obrázku. V centru počítače je aritmeticko-logická
jednotka (ALJ). Činnost celého počítače řídí řadič.
Řadič předává povely operační paměti, ALJ a V/V
zařízením a zpět od nich dostává stavová hlášení.
Řadič čte z operační paměti instrukce, tyto dekóduje a
převádí na posloupnost signálů. Data čte procesor
z operační paměti nebo ze vstupního zařízení; rovněž
tak je odkládá do paměti nebo zapisuje na výstupní
zařízení. Von Neumannův počítač IAS je významný
proto, že až na malé výjimky je jeho schéma platné
dodnes.
Číselné soustavy - obecný úvod
V dobách, kdy byly počítače pomalé, bylo pro hodnocení číselných
soustav důležité, jak pracně se získávají číselné obrazy (tj. převod do
číselné soustavy) a jak pracně se číselné obrazy zpracovávají (tj. náročnost
základních početních operací). U počítačů pro vědecko-technické
výpočty převládaly výpočty nad prováděním V/V operací. Výpočty jsou
charakterizovány velkým množstvím základních početních operací, V/V operace
naopak velkým množstvím převodů mezi číselnými soustavami. Proto pro počítače
pro vědecko-technické výpočty bylo vhodnější použít takovou číselnou
soustavu, ve které se jednodušeji zpracovávají početní operace.
U počítačů pro hromadné zpracování dat (volby, statistika apod.) tomu
bylo obráceně. Dnes jsou rozdíly setřeny.
Polyadické soustavy
Nejznámější polyadickou soustavou je soustava desítková. Číslo se v ní
vyjadřuje jako součet mocnin deseti vynásobených jednoduchými součiniteli.
Součinitelé mohou nabýt některé z hodnot 0,1,...,9 a nazývají se číslice. Číslo
A lze tedy napsat
A=an.10n + an-1.10n-1 +
...... + ai.10i + ..... + a1.101 + a0.100
Běžná je zhuštěná forma zápisu.
A= anan-1 ... ai ... a1a0
Takto lze vyjádřit všechna čísla celá nezáporná. Potřebujeme-li zobecnit
na racionální čísla, zavedeme záporné mocniny až do řádu m.
Vyjádření pak změníme na
A=an.10n + ... + a1.101 + a0.100
+ a-1.10-1 + a-2.10-2 + ... + a-m.10-m
a číslo pak zapisujeme stručně. Takto lze vyjádřit většinu racionálních
čísel. Existují však racionální čísla, která lze přesně vyjádřit jen
nekonečným periodickým výrazem. Je to např. Připustíme-li růst donekonečna,
připustíme tím i vyjádření čísel iracionálních. Jednoznačnost je zde
zachována s výjimkou případů, kdy vyjádření čísla končí nenulovou číslicí,
následovanou nekonečnou řadou nul. Pak lze ve vyjádření nahradit nenulovou číslici
číslicí o jedničku nižší a řadu nul nahradit nekonečnou řadou devítek. Tak
vznikne druhé vyjádření téhož čísla. Tento jev by mohl být považován z hlediska
počítačů za nezajímavý vzhledem k tomu, že délka čísla, zobrazeného
v počítači, musí být vždy konečná. Avšak při algoritmu dělení se
postupně získávají číslice podílu a proces sám o sobě nikdy nekončí. Je ho
třeba zakončit uměle. Tehdy by se mohlo stát, že např. celočíselný podíl bude
vyjádřen druhým způsobem (ovšem ne v nekonečném tvaru).
Zobecnění na záporná čísla zařazením znaménka před číslo je
vhodné pro lidské chápání, nikoli však pro počítač. Při zobecnění
pro jiný základ získáme např. při z=2 dvojkovou - binární
soustavu (vhodná pro vědecko-technické výpočty), při z=8 osmičkovou
- oktalovou soustavu, při z=16 šestnáctkovou - hexadecimální soustavu.
Číslice v těchto soustavách nabývají hodnot . V šestnáctkové soustavě se
číslice 10 až 15 pro přehlednost nahrazují znaky A až F.
Převody mezi polyadickými soustavami
Číslo v soustavě o základu
zk (kde z a k jsou přirozená
čísla) lze převést do soustavy o základu z jednoduše tak, že
každou k-tici číslic nižší soustavy nahradíme číslicí soustavy vyšší.
Jednoduše lze převádět mezi soustavou dvojkovou a osmičkovou nebo mezi dvojkovou a
šestnáctkovou; jednoduše nelze převádět např. mezi dvojkovou a desítkovou. Uveďme
příklad převodu čísla z dvojkové soustavy do šestnáctkové:
0011 1011 01002 = 3B416
Zpětný převod do dvojkové soustavy probíhá tak, že každou číslici
šestnáctkové soustavy převedeme na čtveřici číslic dvojkové soustavy.
Nelze-li uplatnit jednoduchý převod, použijeme obecný algoritmus převodu.
/* Algoritmus pro převod celé části desítkového čísla do soustavy z */
integer i := 0 ; /* Řád číslice */
integer Číslo := celé_číslo_bez_znaménka ; /* Převáděné číslo */
byte Základ := z ;
byte Číslice [] ; /* Vektor převedených číslic */
while Číslo 0
begin
Číslice [i] := Číslo MOD Základ ;
Číslo := Číslo DIV Základ ;
i := i + 1 ;
end;
/* V poli Číslice[0] až Číslice[n] jsou uloženy hodnoty číslic v obráceném
pořadí */
/* Algoritmus pro převod necelé části desítkového čísla do soustavy z */
integer i ; /* Řád číslice */
real Číslo := necelá_část_čísla ; /* Převáděné číslo */
byte Základ := z ;
byte Číslice [] ; /* Vektor převedených číslic */
real Součin ; /* Pracovní proměnná */
for i := 1 to požadovaný_počet_číslic
begin
Součin := Číslo * Základ ;
Číslice := TRUNC ( Součin ) ;
Číslo := Součin - Číslice [i] ;
end;
/* V poli Číslice[1] až Číslice[požadovaný_počet_míst] jsou uloženy hodnoty
číslic necelé části výsledného čísla v přímém pořadí */
Číselné soustavy - v počítačové praxi
- polyadické
- zbytkových tříd
Polyadické soustavy - součet mocnin základu vynásobených číslem
A=an.10n + an-1.10n-1 +
...... + ai.10i + ..... + a1.101 + a0.100
běžná je zhuštěná forma
A= anan-1 ... ai ... a1a0
zobecnění pro racionální čísla
A=an.10n + ... + a1.101 + a0.100
+ a-1.10-1 + a-2.10-2 + ... + a-m.10-m
zobecnění pro záporná čísla - přidáním znaménka (pro počítače
nevhodné)
zobecnění pro komplexní čísla - zavedením imaginární jednotky
Převody mezi soustavami
Viz. obecná část
Číslo v soustavě o základu zk (kde z a k jsou přirozená čísla)
lze převést do soustavy o základu z jednoduše
2 <=> 8 ale ne
8 <=> 16
2 <=> 16 ale ne 2 <=> 10
Každou k-tici číslic nižší soustavy nahradíme číslicí soustavy
vyšší.
Soustavy užívané v počítačové praxi
| z = 2 |
z = 8 |
z = 16 |
dvojková
binární0,1 |
osmičková
oktalová0,1,2,3,4,5,6,7 |
šestnáctková
hexadecimální0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F |
| desítkově |
dvojkově |
osmičkově |
šestnáctkově |
|
|
|
|
| 0 |
00 00 00 |
0 |
0 |
| 1 |
00 00 01 |
1 |
1 |
| 2 |
10 |
2 |
2 |
| 3 |
11 |
3 |
3 |
| 4 |
1 00 |
4 |
4 |
| 5 |
1 01 |
5 |
5 |
| 6 |
1 10 |
6 |
6 |
| 7 |
1 11 |
7 |
7 |
| 8 |
10 00 |
10 |
8 |
| 9 |
10 01 |
11 |
9 |
| 10 |
10 10 |
12 |
A |
| 11 |
10 11 |
13 |
B |
| 12 |
11 00 |
14 |
C |
| 13 |
11 01 |
15 |
D |
| 14 |
11 10 |
16 |
E |
| 15 |
11 11 |
17 |
F |
| 16 |
1 00 00 |
20 |
10 |
| 17 |
1 00 01 |
21 |
11 |
.
.
. |
| 32 |
100000 |
40 |
20 |
Zobrazení celého čísla v počítači v binárním tvaru
| 7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
znaménkový
bit |
|
|
|
|
|
|
|
Zobrazení kladných čísel:
- rozsah zobrazení pro n-bitů <0, 2n-1-1>
pro n=8 <0, 127>
Zobrazení záporných čísel:
- přímý kód : rozsah zobrazení <-2n-1+1, -0>
pro n=8 <-127, -0>, <+0, +1270>
- inverzní kód : inverze bitů (jedničkový doplněk)
- doplňkový kód - operace dvojkový doplněk = inverze bitů a
přičtení jedničky
rozsah zobrazení <-2n-1, 2n-1-1>
pro n=8 <0, 127>
Vztahy mezi zobrazeními
+/- |
Kódová kombinace |
Význam v kódu |
| Přímý |
Inverzní |
Doplňkový |
0
0
0
.
.
0
1
1
:
:
1
1 |
........ 00
........ 01
........ 10
........
........
........ 11
........ 00
........ 01
........
........
........ 10
........ 11 |
0
1
2
.
.
+ MAX
- 0
- 1
.
.
- MAX + 1
- MAX |
0
1
2
.
.
+ MAX
- MAX
- MAX + 1
.
.
-1
-0 |
0
1
2
.
.
+ MAX
- MAX - 1
- MAX
.
:
- 2
-1 |
šířka n-bitů |
|
|
|
Aritmetika ve dvojkových kódech
Základní operace - součet
Přetečení = výsledek operace spadá mimo rozsah zobrazení
Součet v doplňkovém kódu
- všechny bity se sčítají stejně (včetně znaménkového)
- vznikne-li přenos ze znaménkového bitu, tak se ignoruje
- přetečení nastane pokud se přenos do znaménkového bitu nerovná přenosu
ze znaménkového bitu
Příklad:
| 0 |
|
1 |
1 |
0 |
| 0 |
|
1 |
0 |
1 |
|
| 01 |
|
10 |
1 |
1 |
| 1 |
|
0 |
1 |
0 |
| 1 |
|
0 |
1 |
1 |
|
| 10 |
|
01 |
0 |
1 |
Součet v inverzním kódu
problém dvou nul
nutnost provádět tzv. kruhový přenos = přičtení přenosu z nejvyššího
řádu k výsledku
Příklad: -0 + 1
| 1 |
|
1 |
1 |
1 |
| 1 |
|
0 |
0 |
1 |
|
| 0 |
|
0 |
0 |
0 |
|
|
|
+ |
1 |
|
| 0 |
|
0 |
0 |
1 |
Michal Brandejs brandejs@informatics.muni.cz
