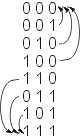
Příklad ztrojení:
P000 Architektura počítačůObsah
|
Kód BCD (Binary Coded Decimal)
4 bity:| 0 | 0 0 0 0 |
| 1 | 0 0 0 1 |
| 2 | 0 0 1 0 |
| 3 | 0 0 1 1 |
| 4 | 0 1 0 0 |
| 5 | 0 1 0 1 |
| 6 | 0 1 1 0 |
| 7 | 0 1 1 1 |
| 8 | 1 0 0 0 |
| 9 | 1 0 0 1 |
| Desítkově | Rozvinutý tvar |
| 7134610 | F7 F1 F3 F4 C616 |
| -7134610 | F7 F1 F3 F4 D616 |
| Desítkově | Rozvinutý tvar |
| 7134610 | 71346C16 |
| -7134610 | 71346D16 |
| Následující:
Vnější, detekční a opravné kódy Obsah |
P000 Architektura počítačůObsah
|
Vnější, detekční a opravné kódy
Vnější kódy
- zavedení nadbytečnosti(redundance)
Parita
- sudá (even)
- lichá (odd)
Kód 2 z 5
| 0 | 0 0 0 1 1 |
| 1 | 0 0 1 0 1 |
| 2 | 0 0 1 1 0 |
| 3 | 0 1 0 1 0 |
| 4 | 0 1 1 0 0 |
| 5 | 1 0 1 0 0 |
| 6 | 1 1 0 0 0 |
| 7 | 0 1 0 0 1 |
| 8 | 1 0 0 0 1 |
| 9 | 1 0 0 1 0 |
Opravné kódy
Příklad ztrojení:
| Následující:
Kódová vzdálenost a její zobrazení Obsah |
P000 Architektura počítačůObsah
|
Kódová(Hammingova) vzdálenost
Kódová vzdálenost d = počet bitů, v nichž se liší dvě sousední platné kódové kombinace.
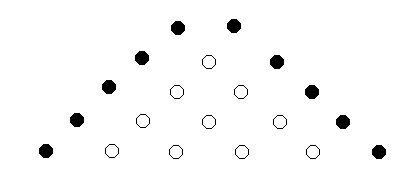
Znázornění pomocí Hammingovy krychle
- trojrozměrná (xyz)
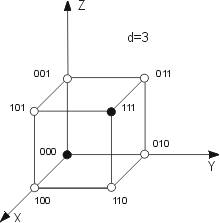
- dvojrozměrná (xy)
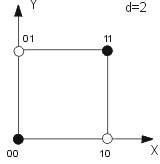
- jednorozměrná (x)
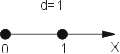
| Následující:
Vztah kódové vzdálenosti a počtu chyb Obsah |
P000 Architektura počítačůObsah
|
Detekce a oprava k chyb
| Detekce k chyb: | d>=k+1 |
| Oprava k chyb: | d>=2k+1 |
Jiné znázornění: |
| d | detekce | oprava |
| 1 | 0 | 0 |
| 2 | 1 | 0 |
| 3 | 2 | 1 |
| 4 | 3 | 1 |
| 5 | 4 | 2 |
| Následující:
Booleova algebra Obsah |
P000 Architektura počítačůObsah |
Booleova algebra
GEORGE BOOLE (1815 - 1864) - Irský matematik, v roce 1854 zvláštní druh algebry (uplatnění až v roce 1938).
Boolova algebra je nauka o operacích na množině {0,1}.
Způsoby popisů:
- Pravdivostní tabulka
- Graficky v rovině = Vennovy diagramy
- Matematický aparát
B. A. užívá jen 3 základní operace:
- Logický (Booleův) součin AND
x (bez)
- Logický (Booleův) součet OR

+
- Negace
NOT
~(před operandem)
Pravdivostní tabulka:
a b a + b a . b 0 0 0 0 1 0 1 1 0 1 1 0 1 0 0 1 1 1 1 0 Vennovy diagramy:
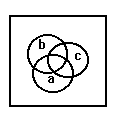
Def.: B.A. je množina B o alespoň 2 prvcích nad níž jsou definovány operace operace sčítání, násobení a negace splňující tyto axiomy:
(předp.: a, b, c
B) :
a + bB
a . bB
Existuje prvek 0, pro který platí: a + 0 = a
Existuje prvek 1, pro který platí: a . 1 = a
Komutativní zákon:
a + b = b + a
a . b = b . a
a + (b . c) = (a + b) . (a + c)
a . (b + c) = (a . b) + (a . c)
Pro každý prvek a existuje prvekB:
a .= 0
a += 1
| Následující: Obvodové
znázornění Booleovy algebry Obsah |
P000 Architektura počítačůObsah |
Obvodové znázornění B-algebry
Pravidla pro kresbu značek:
- Vstup je vždy zleva, výstup zprava
- Značky se nesmějí otáčet
- Spoje mají být rovnoběžné s okraji listu
Minimalizace počtu operací B-algebry
1. Matematické úpravy
Př:
2. Využitím jednotkové krychle
3. Karnaughova mapa normalizací Vennova diagramu
Pro vyšší řády nejsou souvislé prostory proměnných.
Př:
B-algebra je nevhodná pro technickou realizaci - příliš velký počet operací (.,+,
)
| Následující: Shefferova
algebra, Peirceova algebra Obsah |
P000 Architektura počítačůObsah |
Shefferova algebra
Je vybudovaná na jedné logické funkci = negace logického součinu NAND.
Pro libovolný počet proměnných
Pravidla:
Pomocí operace NAND lze realizovat všechny operace Booleovy algebry.
Neplatí zákon komutativní:
Neplatí zákon asociativní:
Peirceova algebra
Vystavěna na operaci NOR (negace logického součtu) - obdobné jako S-algebra.
Převod minimalizované formy B-algebry na S-algebru:
Opakovanou aplikací de Morganových pravidel:
Př.:
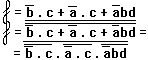
Obvodové znázornění S-algebry:
Obvodové znázornění P-algebry:
| Následující: Fyzikální
podstata signálů Obsah |
P000 Architektura počítačůObsah |
Fyzikální podstata signálů
HLADINOVÉ
RELÉ
IMPULSOVÉ
AMPLITUDA
KMITOČET
FÁZE
Magnetické obvody
Hodnoty jsou stanoveny pro každou výrobní technologii zvlášť.
L ~ 0 H ~ 1 .........................pozitivní logika
L ~ 1 H ~ 0 .........................negativní logika
| Následující: Technologie
TTL Obsah |
P000 Architektura počítačůObsah |
Technologie TTL
(tranzistor-tranzistor logic)
Základní stavebí prvek je tranzistor NPN.
Parametry TTL:
napájecí napětí + 5V
Invertor v TTL:
NAND pomocí dvou tranzistorů: NOR: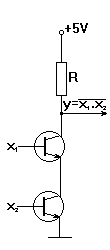
x1 x2 NAND x1 x2 NOR 0 0 1 0 0 1 0 1 1 0 1 0 1 0 1 1 0 0 1 1 0 1 1 0
| Následující: Kombinační
logické obvody Obsah |
P000 Architektura počítačůObsah |
Kombinační logické obvody
Základní logické členy:
USA DINInvertor:
AND:
OR:
NAND:
NOR:
Př.: NOR
x1 x2 y 0 0 1 0 1 0 1 0 0 1 1 0
| Následující: Ostatní
logické členy Obsah |
P000 Architektura počítačůObsah |
Ostatní logické členy
Nonekvivalence - XOR
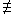
= 1
x1 x2 y 0 0 0 0 1 1 1 0 1 1 1 0 y = x1 x2
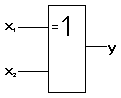
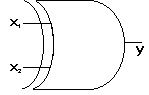
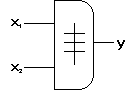
Př. Generátor parity: y = a
b
c
d = (a
b)
(c
d)
Schématická značka:
Ekvivalence - NOXOR
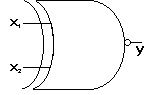
| Následující: Logické
obvody Obsah |
P000 Architektura počítačůObsah |
Logické obvody
Multiplexor Z = A . X +
. Y
4-vstupý multiplexor
4 datové vstupy
2 adresové vstupy
A1 A2 Q 0 0 D0 0 1 D1 1 0 D2 1 1 D3 Q = .
. D0 +
. A2 . D1 +
+ A1 .
. D2 + A1 . A2 . D3
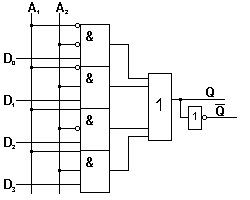
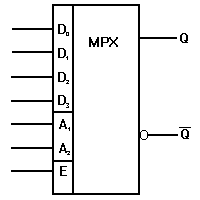
ENABLE
| Následující: Dekodér,
sčítačky Obsah |
P000 Architektura počítačůObsah |
Dekodér
D0 = .
D1 = . A2
D2 = A1 . D3 = A1 . A2
Realizace MPX pomocí dekodéru:
Sčítačky
Sčítačka MODULO 2 x + y = z
1. Tabulka:
x y z 0 0 0 0 1 1 1 0 1 1 1 0 2. Rovnice:
z =
. y + x .
Polosčítačka
x y S P 0 0 0 0 0 1 1 0 1 0 1 0 1 1 0 1 S = . y + x .
P = x . y
| Následující: Úplná
sčítačka, vícemístná sčítačka Obsah |
P000 Architektura počítačůObsah |
Úplná sčítačka
xi yi pi <-- pi-1 <--
si
xi yi pi-1 si pi 0 0 0 0 0 0 0 1 1 0 0 1 0 1 0 0 1 1 0 1 1 0 0 1 0 1 0 1 0 1 1 1 0 0 1 1 1 1 1 1 Vícemístná sčítačka
| Následující: Sekvenční
logické obvody Obsah |
P000 Architektura počítačůObsah |
Sekvenční logické obvody
Sekvenčví obvod:
Základní paměťový člen:
Klopný obvod RS
R.......RESET (nulování)
S.......SET (nastavení)
R S Qi 0 1 1 0 1 0 0 1 0 0 Qi-1 1 1 Zakázaný stav Obvod řízený jedničkami.
RS řízený nulami:
Qi 1 0 1 0 1 0 1 1 Qi-1 0 0 Zakázaný stav
Obvod RS řízený jedničkami s časovou synchronizací.
Klopný obvod řízený
HLADINOU:
- horní
- dolní
HRANOU:
- čelem impulsu (nástupní hrana)
- týlem impulsu (sestupná hrana)
| Následující: Klopný
obvod D, klopný obvod JK Obsah |
P000 Architektura počítačůObsah |
Klopný obvod D
D ....delay (vzorkovací K.a)
D C Qi 1 1 0 0 ? __ Qi-1 Realizace D-KO pomocí RS:
Klopný obvod JK
J K Qi 0 1 0 1 0 1 0 0 Qi-1 1 1
U většiny KO navíc:
R....reset
| Následující: Přenos
informací v systému Obsah |
P000 Architektura počítačůObsah |
Přenos informací v systému
Sériový:
Paralelní:
Převod sériová informace -> paralelní
pomocí posuvného registru
Uvnitř počítače přenos paralelně pomocí sběrnice.
Využití paralelních registrů
| Následující: Sčítačka v
BCD kódu Obsah |
P000 Architektura počítačůObsah |
Sčítačka v BCD kódu
Součet dvou čísel vyjádřený:
Dvojkově: BCD: Desítkově 0 0000 0 0000 0 0 0001 0 0001 1 .
.
.
.
.
.
.
.
.
0 1001 0 1001 9 0 1010 1 0000 10 0 1011 1 0001 11 0 1100 1 0010 12 0 1101 1 0011 13 0 1110 1 0100 14 0 1111 1 0101 15 1 0000 1 0110 16 1 0001 1 0111 17 1 0010 1 1000 18 1 0011 1 1001 19
| Následující: Typické
sekvenční obvody v počítačích Obsah |
P000 Architektura počítačůObsah |
Typické sekvenční obvody v počítačích
Seriová sčítačka:
Paralelní registr = střádač:
Sériový registr (posuvný registr):
Jedním taktem signálu CLK se informace posune o jeden D-KO.
Čítače:
Dvojkový čítač 0...15, 0...15, ...
Řízen sestupnou hranou impulsu.
| Následující: Násobičky Obsah |
P000 Architektura počítačůObsah |
Násobičky
Sekvenční násobení (bez znaménka)
NÁSOBENEC
REGISTR +
STŘÁDAČ
NÁSOBITEL
REGISTR
i ČÍTAČ
MAX 0
Kombinační násobička
| Následující: Rotace bitů,
logický a aritmetický posun Obsah |
P000 Architektura počítačů |
Rotace bitů Doleva Doprava Logický posun (Logical shift) Doleva Doprava Aritmetický posun (Arithmetic shift) Doleva Znaménkový bit se nemění !
~ násobení x2
Doprava Znaménkový bit se kopíruje do nižšího řádu.
~ dělení :2
Blok operační jednotky
| Následující: Obvod pro
rotaci bitů vpravo, vlevo a beze změny, komparátor Obsah |
P000 Architektura počítačůObsah |
Obvod pro rotaci vlevo, vpravo a beze změny
Komparátor
| Následující:
Paměti Obsah |
Michal Brandejs brandejs@informatics.muni.cz