Psychometrika: měření v psychologii

Řešené příklady

Zadání

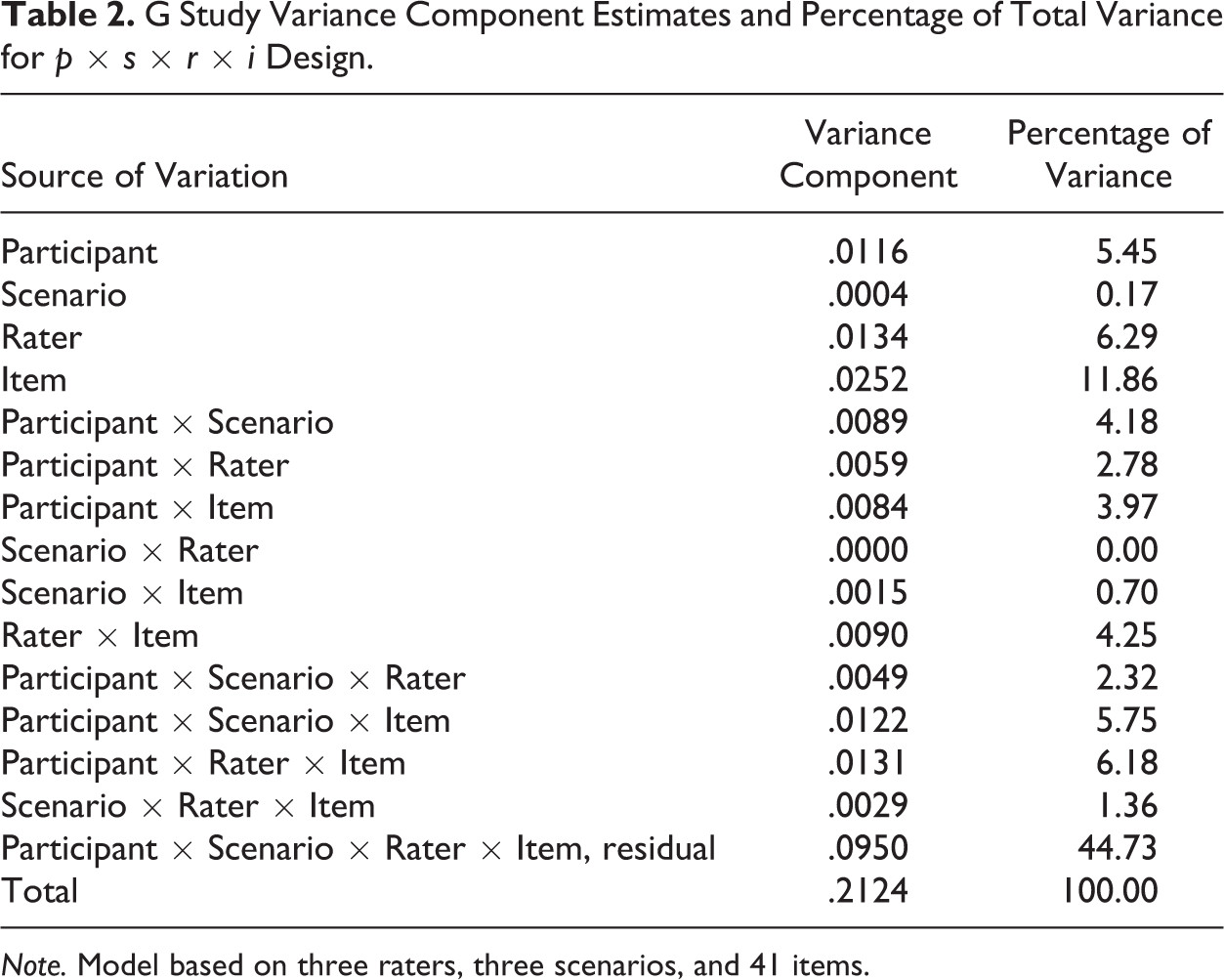
V níže citovaném článku popisují využití teorie zobecnitelnosti v případě, kdy tři hodnotitelé hodnotili ve třech scénářích 18 zdravotních sester pomocí 41 kritérií. Článek nečtěte! :-) Zamyslete se ale nad následujícími třemi otázkami:

  1. Podívejte se na tabulku 2. Dokázali byste spočítat koeficienty dependability a zobecnitelnosti pro různé designy? Co kdyby posouzení realizovalo pět hodnotitelů ve 20 kritériích, ale v rámci jediného scénáře; cílem by bylo participanty prostě jen seřadit, a studie by proto byla relativní?
  2. Co kdyby byl scénář stejný jako předtím, kritéria by byla stále relativní, ale chtěli byste zobecňovat na prostor všech možných hodnotitelů i scénářů?
  3. Při pohledu na obrázek 1 se vám zdá výhodnější zvyšovat počet hodnotitelů, nebo počet scénářů (klíčová je časová zátěž hodnotitelů, časová zátěž sester vás příliš netrápí)? Jaký počet hodnocení se zdá být ideální? Počítejte s pevným počtem 41 položek. 

table2.jpeg

figure1.jpeg

Nemusíte odpovídat, stačí se zamyslet. Pokud to zkusíte spočítat, napište výsledek; pokusím se vám dát zpětnou vazbu. Každopádně podobný příklad se může vyskytnout v písemném testu.

O’Brien, J., Thompson, M. S., & Hagler, D. (2019). Using Generalizability Theory to Inform Optimal Design for a Nursing Performance Assessment. Evaluation & the Health Professions, 42(3), 297–327. https://doi.org/10.1177/0163278717735565 

Plný text článku k průběžnému úkolu
O’Brien, J., Thompson, M. S., & Hagler, D. (2019). Using Generalizability Theory to Inform Optimal Design for a Nursing Performance Assessment. Evaluation & the Health Professions, 42(3), 297–327. https://doi.org/10.1177/0163278717735565

Řešení

R=Rater, I=Item (kritérium), S=Scenario.

Obecná pravidla: 

  1. Relativní fasety nejsou chybovými složkami. 
  2. Absolutní fasety jsou chybovými složkami.
  3. Interakce relativních faset navzájem nejsou chybovými složkami.
  4. Interakce jakékoli fasety s objektem měření je chybovou složkou.
  5. Jakákoli Interakce s absolutní fasetou je chybovou složkou.

Prosím, neučte se ta pravidla nazpaměť; jsou veskrze logická a napsal jsem je na koleně :-)

Příklad 1: 5 hodnotitelů, 20 kritérií, 1 scénář. Relativní D-studie.

D-studie zahrnuje tři fasety s designem R×I×S. Podle zadání má být relativní, a proto nehraje roli výběr hodnotitelů, kritérií ani scénáře, které jsou konstantní pro všechny osoby (a na jejich pořadí tak nemají vliv). Ve zcela relativní studii nehraje roli ani interakce fixovaných zdrojů rozptylu; například interakce pěti (relativních) hodnotitelů a 20 (relativních kritérií) je shodná pro všechny respondenty, a není proto chybovým rozptylem. Jinými slovy, chybovým rozptylem jsou pouze ty komponenty, které nabývají rozdílných hodnot pro jednotlivé respondenty; jde o ty komponenty, které zahrnují interakci s respondenty. Interpretace takovéhoto koeficientu by byla očekávaná korelace paralelních testů v případě, kdy by těch stejných pět hodnotitelů hodnotilo stejné respondenty ve stejných 20 položkách a stejném scénáři za předpokladu, že by se mezi situacemi nic nezměnilo, resp. by situace byly zcela paralelní (což nelze očekávat, reálně bychom museli zahrnout novou fasetu, situaci, a do modelu ji zapracovat).

Relativní chybový rozptyl:

\sigma_\delta^2 = \frac{\sigma_{ps}^2}{1\times1} + \frac{\sigma_{pr}^2}{1\times5} + \frac{\sigma_{pi}^2}{1\times20} + \frac{\sigma_{psr}^2}{1\times1\times5} + \frac{\sigma_{psi}^2}{1\times1\times20} + \frac{\sigma_{pri}^2}{1\times5\times20} + \frac{\sigma_{psri, e}^2}{1\times1\times5\times20} = \\ = \frac{.0089}{1} + \frac{.0059}{5} + \frac{.0084}{20} + \frac{.0049}{5} + \frac{.0122}{20}+ \frac{.0131}{100} + \frac{.0950}{100} = .013171

Koeficient zobecnitelnosti je nedostatečný:

Zhruba by šel odečíst z grafu (G koeficient, pět hodnotitelů, spodní řádek s 1 scénářem), kde je však odhadnut pro plný počet 41 položek. 

Příklad 2: 5 hodnotitelů, 20 kritérií, 1 scénář. Smíšená D-studie.

Design je stejný jako v předchozím případě, jen hodnotitelé i scénáře jsou absolutními fasetami, zatímco kritéria zůstávají relativní. Výsledkem tedy bude očekávaná korelace paralelních testů, pokud by těm stejným respondentům bylo vylosováno pět nových hodnotitelů a zcela nový scénář (kritéria se ale nezmění, nechceme zobecňovat na prostor všech možných kritérií). Chybový rozptyl budou tvořit všechny komponenty, které se liší pro různé respondenty; jedinou výjimkou je tedy samotná faseta kritéria, která zůstává konstantní. Absolutní chybový rozptyl by v tomto případě byl

\sigma_\Delta^2 = \frac{\sigma_{s}^2}{1} + \frac{\sigma_{r}^2}{5\times1} + \frac{\sigma_{ps}^2}{1\times1} + \frac{\sigma_{pr}^2}{1\times5} + \frac{\sigma_{pi}^2}{1\times20} + \frac{\sigma_{sr}^2}{1\times5} + \frac{\sigma_{si}^2}{1\times20} + \frac{\sigma_{ri}^2}{5\times20} + \frac{\sigma_{psr}^2}{1\times1\times5} + \frac{\sigma_{psi}^2}{1\times1\times20} + \frac{\sigma_{pri}^2}{1\times5\times20} + \frac{\sigma_{sri}^2}{1\times5\times20} + \frac{\sigma_{psri, e}^2}{1\times1\times5\times20} = \\ \frac{.0004}{1} + \frac{.0134}{5} + \frac{.0089}{1} + \frac{.0059}{5} + \frac{.0084}{20} + \frac{0}{5} + \frac{.0015}{20} + \frac{.0090}{100} + \frac{.0049}{5} + \frac{.0122}{20} + \frac{.0131}{100} + \frac{.0029}{100} + \frac{.0950}{100} = .016445

Koeficient dependability je sice ještě nižší, nikoli však příliš, \Phi=\frac{.0116}{.0116+.016445} = .414.

Zde chci upozornit, že zvolený design nemá příliš smysl a hlavně jen málo praktického využití. Hodnotitelé skutečně mohou být náhodní, je ale otázkou, zda má smysl za náhodnou (absolutní) fasetu považovat i scénáře.

Příklad 3: Optimální design D-studie

Osobně bych s pomocí grafu došel k závěru, že nemá smysl zvyšovat počet scénářů nad tři, možná (v případě relativní D-studie) nad čtyři. Stejně tak bych volil jen tři až pět hodnotitelů. Pokud by cílem bylo přijímací řízení a tedy ryze relativní D-studie, pak bych volil 3 hodnotitele a čtyři scénáře; scénáře bych držel vždy jako fixní fasetu. Pokud by se hodnotitelé různili, pak bych volil spíše pět hodnotitelů a tři scénáře. To ale záleží ale na individuálním názoru, je potřeba uvažovat o cíli takového měření, a pro to je v zadání relativně málo informací. 

Písemný test

Tento příklad je velmi náročný, obsahuje hodně komplikovaných faset. Můžete očekávat, že příklad v průběžném testu bude o něco jednodušší; přišlo mi to lepší než naopak. Pokud tento příklad pochopíte a dokážete celý postup sledovat, písemný test bude hračka ;)

Předchozí
Následující