I. Eukleidovské konstrukce

Seznámení s eukleidovskými konstrukcemi, tzn. s konstrukcemi užívajícími pouze pravítka (bez značek) a kružítka. 

Zejména věnujeme pozornost konstrukci kolmice a rovnoběžky včetně zdůvodnění (dále ovšem používáme obvyklé zkratky s ryskami apod.)

V úloze s omezenou nákresnou poprvé používáme vhodné transformace, např.

Úlohu bez pravítka uvádíme pro zajímavost.

II. Kvadratura mnohoúhelníku

Konstrukce čtverce, který má stejný obsah jako daný mnohoúhelník.

Základní úlohy jsou:

• transformace trojúhelníku na rovnoběžník (obdélník)
• transformace rovnoběžníku na rovnoběžník (obdélník) s danou stranou
• transformace obdélníku na čtverec (pomocí Eukleidových vět)

Sčítání dílčích nápadů u obecného mnohoúhelníku lze dělat různě, např. takto:

Poznámky ke stříhání uvádíme pro zajímavost.

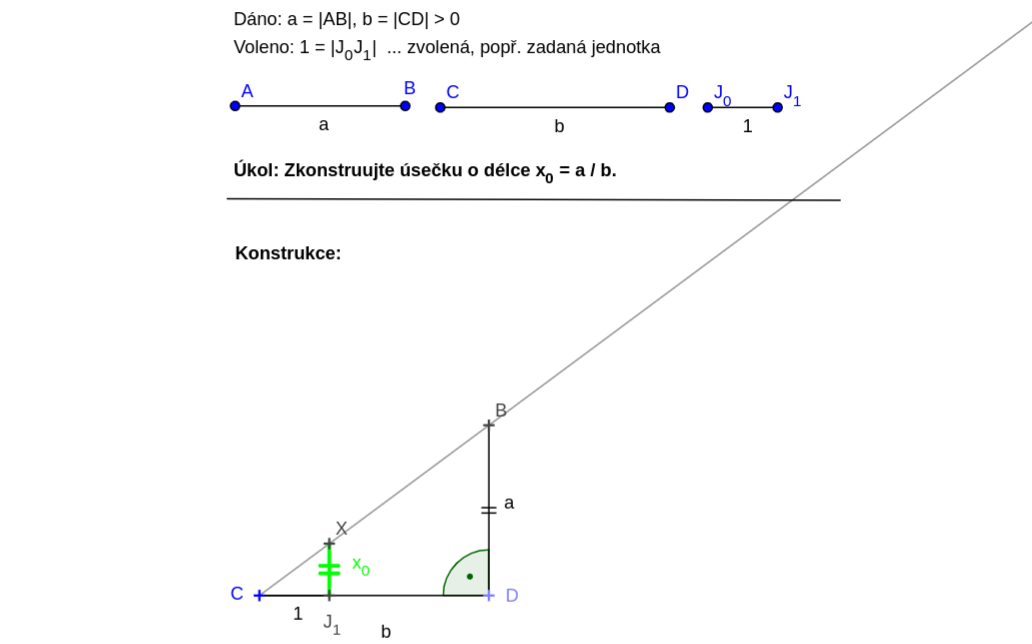
III. Zlatý řez a algebra

Konstrukce vs. počítání  charakterizace eukleidovsky sestrojitelných veličin.

Konstrukci zlatého řezu interpretujeme jako konstrukci kořene (speciální) kvadratické rovnice.

Sestrojitelné veličiny odpovídají kořenům kvadratických rovnic se sestrojitelnými koeficienty...
... tedy z dané jednotky se  k nim lze dopracovat pouze pomocí operací

IV. Pravidelné mnohoúhelníky

Co víme o pravidelných mnohoúhelnících a které lze sestrojit?

Zejména věnujeme pozornost pravidelnému pětiúhelníku, což je první mnohoúhelník zasluhující soustředěnou pozornost.
Jeho konstrukce je ekvivalentní konstrukci zlatého řezu:

Kombinací předchozích nápadů lze sestrojit další mnohoúhelníky (viz např. 12 = 3.4 = 2.6}.
Většinu mnohoúhelníků sestrojit nelze!