Kosmologické minimum
Současné kosmologické modely jsou založeny na obecné teorii relativity. Chování vesmíru v těchto modelech lze vak vysvětlit i na základě představ blízkých newtonovské fyzice. Tyto představy dovolují odvození základních rovnic, názornou interpretaci jejich členů a objasnění chování vesmírů na základě grafické reprezentace.
Úvod
Kosmologie byla dlouho považována za poněkud nedůvěryhodné odvětví fyziky, jak je vidět u z toho, že její otcové-zakladatelé Fridman, Lemaitre, Hubble, Gamow nebyli odměněni Nobelovou cenou. O změně postoje ke kosmologii svědčí zkracování intervalů mezi Nobelovými cenami : Penzias a Wilson, reliktní záření, objev 1964, cena 1978; Mather a Smoot, černotělové spektrum reliktního záření, objev 1992, cena 2006; Perlmutter, Schmidt a Riess, zrychlené rozpínání vesmíru, objev 1998, cena 2011.
Projevuje se tu zřejmě zvýšení možnosti získávání nových, přesných a spolehlivých dat díky kosmickým sondám a jejich přístrojovému vybavení, ale také pokrok fyziky mikrosvěta, který umožňuje uskutečnit v pozemských laboratořích procesy předpokládané v raném vesmíru. Nové objevy stále dobře zapadají do obecné teorie relativity, poukazují však na základní omezenost našich znalostí o chování hmotné náplně vesmíru: baryonová hmota (baryony - částice reagující na silnou interakci, s poločíselným spinem) svítící ve hvězdách a známá z pozemských laboratoří tvoří jen několik procent celkové energie vesmíru.
Tyto objevy a otázky s nimi spojené podněcují zájem o kosmologii, který bude nepochybně narůstat a zasahovat i veřejnost a studenty středních kol. Je proto vhodné se zamýšlet nad tím, nakolik mohou být zpřístupněny způsobem, který se neomezuje jen na sdělení faktů, ale dovoluje i hlubší pochopení jejich souvislostí. Že to není nemoné, pokusíme se naznačit v dalším.
Kosmologický princip
Současné kosmologické modely se zakládají na předpokladu, kterému se říká kosmologický princip. Podle něho může být vesmír vyplněn fundamentálními pozorovateli, kteří sdílejí pohyb hmotné výplně a kterým se vesmír jeví (po středování ve velkém prostorovém i časovém měřítku) stejně. To znamená, že tito pozorovatelé se shodují na tom, co je pro ně současné: současné jsou pro ně události, které nastávají ve stejném stádiu vývoje vesmíru a v této současnosti je pro ně vesmír homogenní a isotropní (stejný ve všech místech a ve všech směrech). Z našeho místa ve vesmíru lze dobře ověřovat jeho isotropii a spojení výsledků pozorování s teorií umožňuje, i když s menší jistotou, usuzovat i na homogenitu.
Kosmologického principu poprvé použil Einstein roku 1917. Domníval se však, že vesmír by měl být nejen homogenní a isotropní, ale (ve velkém měřítku) i časově neproměnný (dokonalý kosmologický princip). Protože jeho rovnice v původním tvaru z roku 1915 tomuto požadavku nevyhovovaly, doplnil je tzv. kosmologickým členem. Později Fridman a nezávisle na něm Lemaitre vyřeili kosmologický problém i bez předpokladu statičnosti vesmíru. K dokonalé matematické formě dovedli řešení založené na kosmologickém principu Robertson a Walker proto FLRW modely. V rámci obecné teorie relativity tyto modely vyčerpávají všechny možnosti pro prostoročasovou geometrii vesmíru splňujícího kosmologický princip.
Newtonovská kosmologie
Zdálo by se, že newtonovská fyzika neumožňuje vybudovat kosmologii, která by souhlasila s kosmologickým principem. Homogenní a isotropní rozložení hmoty v eukleidovském prostoru vede k tomu, že hmota se protírá do nekonečna a výpočet intenzity gravitačního pole v kterémkoliv místě vede k neurčitému výrazu. Tato potíž, na ni narážel již Newton a jeho následovníci, však může být překonána, jak ukázal roku 1931 Milne. Na základě jednoduché myšlenky, kterou vyjadřuje Obr. 1, z Newtonova gravitačního zákona plyne, e homogenní kulová tenká slupka nepřispívá ke gravitačnímu poli ve svém vnitřku.
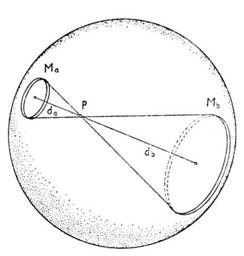
Obr.1 Gravitační působení kulové slupky vyplněné látkou o konstantní hustotě na hmotný bod P je nulové[1]
Představme si nyní, že koule na obrázku představuje část vesmíru dostatečně velkou na to, abychom mohli počítat s platností kosmologického principu. Pak vnější vesmír si můžeme představit rozložený do soustředných slupek, které podle předchozího nepřispívají ke gravitaci uvnitř. Element výplně vesmíru o hmotnosti ![]() (v realitě galaxie) na okraji koule se proto řídí pohybovou rovnicí
(v realitě galaxie) na okraji koule se proto řídí pohybovou rovnicí
![]()
kde ![]() je vzdálenost od středu,
je vzdálenost od středu, ![]() hmotnost obsaená v kouli,
hmotnost obsaená v kouli, ![]() gravitační konstanta, tečkou značíme derivaci podle času. Můžeme vyjít také ze zákona zachování energie pro daný element
gravitační konstanta, tečkou značíme derivaci podle času. Můžeme vyjít také ze zákona zachování energie pro daný element
![]()
jeho derivováním podle času a vykrácením dostaneme pohybovou rovnici (1) za předpokladu, že ![]() .
.
(Statický vesmír vyhovuje rovnici (2), ale nikoliv rovnici (1)).
Uvažujme nyní o vesmíru v nějakém počátečním čase ![]() , v něm pozorovatel ve středu koule zaznamenává potřebná data. Položme
, v něm pozorovatel ve středu koule zaznamenává potřebná data. Položme
![]()
![]() probíhá počáteční polohy galaxií a
probíhá počáteční polohy galaxií a ![]() je škálový faktor vyjadřující změny vzdáleností ve vesmíru v čase (jeho rozpínání či smršťování) v čase.
je škálový faktor vyjadřující změny vzdáleností ve vesmíru v čase (jeho rozpínání či smršťování) v čase.
Dosazením do (1) a vykrácením ![]() a
a ![]() dostaneme
dostaneme ![]()
kde![]() je počáteční hustota hmotnosti. Obdobně rovnice (2) můe být přepsána jako první integrál rovnice (4),
je počáteční hustota hmotnosti. Obdobně rovnice (2) můe být přepsána jako první integrál rovnice (4),
(5) ![]() ,
,
kde ![]() je integrační konstanta. Statické řešení (5) je opět vyloučeno rovnicí (4).
je integrační konstanta. Statické řešení (5) je opět vyloučeno rovnicí (4).
Rovnice (4), resp. (5) pro škálový faktor v sobě zahrnují pohyb kadého jeho elementu a tedy i kadého fundamentálního pozorovatele spojeného s tímto elementem. Vidíme z nich, že počáteční homogenita a isotropie vesmíru není jeho vývojem narušena. Rychlost vzdalování každého elementu od zvoleného počátku je úměrná jeho vzdálenosti podle vztahu,
(6), ![]()
kde ![]() se nazývá Hubbleova konstanta (v čase ovšem konstantní není).
se nazývá Hubbleova konstanta (v čase ovšem konstantní není).
Proti newtonovské kosmologii může být vznesena námitka, která patrně bránila jejímu dřívějímu vzniku (rovnice (1), (3) mohl odvodit ji Newton). Na první pohled se zdá, že tato kosmologie privileguje postavení centrálního pozorovatele, kolem něhož se vesmír smršťuje či rozpíná. Ve skutečnosti se takto jeví vesmír každému fundamentálnímu pozorovateli. Namísto Newtonova absolutního prostoru či souboru rovnoprávných inerciálních soustav zavádí newtonovská kosmologie privilegovanou soustavu spojenou se středním pohybem kosmické hmoty. Další vlastností, která odlišuje newtonovskou kosmologii od speciální teorie relativity, je to, že se v ní dá mluvit o privilegované současnosti a privilegované časové souřadnici (kosmickém čase), jež jsou společné pro všechny fundamentální pozorovatele.
Kosmologický člen
Úspěch přechodu od rovnic pro galaxie (1), (2) k rovnicím pro vesmír (4),(5) se zakládal na krácení veličinou ![]() (rovnost hmotnosti tíhové a setrvačné) a veličinou
(rovnost hmotnosti tíhové a setrvačné) a veličinou![]() , které je umožněno speciálním tvarem Newtonova gravitačního zákona. Tento přechod od částí k celku nebude narušen, přidáme-li na pravou stranu rovnice (1) člen úměrný vzdálenosti, takže pohybová rovnice bude
, které je umožněno speciálním tvarem Newtonova gravitačního zákona. Tento přechod od částí k celku nebude narušen, přidáme-li na pravou stranu rovnice (1) člen úměrný vzdálenosti, takže pohybová rovnice bude
(7) ![]()
veličina ![]() se nazývá kosmologická konstanta. Rovnice (4), (5) pak můžeme doplnit na tvar zahrnující vliv kosmologického členu
se nazývá kosmologická konstanta. Rovnice (4), (5) pak můžeme doplnit na tvar zahrnující vliv kosmologického členu
(8) ![]()
(9) ![]()
Rovnice (7), (8) nyní umoňují i statické řešení.
Omezíme-li FLRW modely předpokladem, že hmota vyplňující vesmír je nekoherentní prach s nulovým tlakem, vedou Einsteinovy rovnice s případně nenulovým kosmologickým členem k rovnicím, které jsou zcela identické s rovnicemi newtonovské kosmologie (8), (9). V newtonovské kosmologii není předpoklad o nulovosti tlaku podstatný, protoe tlak sám o sobě neovlivňuje pohyb hmotných elementů ten by mohl ovlivnit jen jeho gradient, který je na základě předpokladu o homogenitě a isotropii nulový. V obecně relativistické kosmologii ovem tlak vstupuje do Einsteinových rovnic a newtonovská kosmologie se proto stává nepoužitelnou při vyšší koncentraci hmoty (v raných fázích vývoje vesmíru). Hmotnou výplň současného vesmíru (nejen svítící či baryonovou, ale i vekerou hmotu částicové povahy) vak můžeme vzhledem k její malé hustotě považovat za nekoherentní prach s nulovým tlakem, take základní chování vesmíru v newtonovské kosmologii (popřípadě s kosmologickým členem) se nelií od chování předvídaného obecnou teorií relativity.
Hubbleova a další pozorování červeného posuvu spekter galaxií vedla k závěru, že vesmír není statický a zavedení kosmologického členu bylo tedy zbytečné. Nová pozorování však napovídají, že jeho zavedení je nejjednodušším způsobem, jak vysvětlit zrychlené rozpínání vesmíru. Kosmologický člen bývá interpretován jako vyjádření fyzikálních vlastností vakua (nejnižšího energetického stavu hmoty). Vakuum se pak vyznačuje kladnou hustotou energie a záporným tlakem (čili napětím). Hustota energie a tlaku vakua se podle Einsteinových rovnic rozpínáním nemění. Z newtonovského hlediska kosmologický člen s kladným ![]() způsobuje, že na galaxie působí (z hlediska centrálního pozorovatele)kromě newtonovské gravitace ještě kosmologická síla úměrná vzdálenosti. Pro danou vzdálenost zůstává tato síla konstantní na rozdíl od newtonovské gravitace, která při rozpínání vesmíru s časem klesá a v daném čase je nepřímo úměrná kvadrátu vzdálenosti.
způsobuje, že na galaxie působí (z hlediska centrálního pozorovatele)kromě newtonovské gravitace ještě kosmologická síla úměrná vzdálenosti. Pro danou vzdálenost zůstává tato síla konstantní na rozdíl od newtonovské gravitace, která při rozpínání vesmíru s časem klesá a v daném čase je nepřímo úměrná kvadrátu vzdálenosti.
Zahrada kosmologických modelů
Rovnice (8) obsahuje tři konstanty, ![]() . Různým hodnotám těchto konstant odpovídají různá řešení rovnice a tedy z hlediska pozorovatele v čase
. Různým hodnotám těchto konstant odpovídají různá řešení rovnice a tedy z hlediska pozorovatele v čase ![]() , kdy škálový faktor byl volen rovným jedné, různé vývoje vesmíru. Při jiné volbě počátečního času by se změnila hodnota škálového faktoru jeho vynásobením multiplikativní konstantou faktory
, kdy škálový faktor byl volen rovným jedné, různé vývoje vesmíru. Při jiné volbě počátečního času by se změnila hodnota škálového faktoru jeho vynásobením multiplikativní konstantou faktory![]() a
a ![]() , kde
, kde ![]() , odpovídají tedy témuž modelu, ale s jiným postavením pozorovatele v čase.
, odpovídají tedy témuž modelu, ale s jiným postavením pozorovatele v čase.
Pro porovnání s realitou potřebuje proto pozorovatel tři údaje spojené s pozorováním, která také v principu může obdržet na základě statistického zpracování dat o závislosti mezi svítivostmi objektů a jejich červenými posuvy.

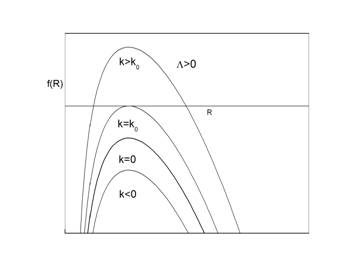
Obr.2{C} Zahrada kosmologických modelů podle [2]
Na Obr.2 jsou znázorněny různé typy závislosti kálového faktoru (svislá osa) na čase (vodorovná osa). Jako ![]() je označena kosmologická konstanta v jednotkách obvykle pouívaných v obecné teorii relativity a
je označena kosmologická konstanta v jednotkách obvykle pouívaných v obecné teorii relativity a ![]() je podle této teorie křivost třírozměrného prostoru řezu prostoročasem tvořeného současnými událostmi. S veličinami
je podle této teorie křivost třírozměrného prostoru řezu prostoročasem tvořeného současnými událostmi. S veličinami ![]() a
a ![]() zavedenými v newtonovské kosmologii souvisí vztahy
zavedenými v newtonovské kosmologii souvisí vztahy
(10) ![]() ,
,
kde ![]() je rychlost světla.
je rychlost světla.
Pozoruhodnou vlastností většiny uvedených modelů je existence singularit vesmíry startují ze stavu s nulovým škálovým faktorem a tedy s nekonečnou hustotou hmotnosti. Jak již bylo řečeno, v okolí singularit je newtonovská kosmologie nepoužitelná a je třeba se obrátit k obecné teorii relativity a poznatkům o fyzice mikrosvěta. I tak ovšem (aspoň při současné úrovni poznání) se při postupu k singularitě závěry fyziky stávají stále nejistějšími a k samotné singularitě nedosáhneme.
Protože uvažované kosmologické rovnice nepreferují žádný směr času, mohli bychom doplnit Obr.2 také grafy časových vývojů, které by singularitou nezačínaly, ale pouze končily. Takové modely jsou ve zřejmém rozporu s realitou (podle pozorování se vesmír rozpíná) a lze proti nim vznášet i námitky filosofické povahy (jak může vesmír s nekonečnou minulostí zaniknout?). To je zřejmě důvod, proč nejsou na Obr. 2 uvažovány.
Pohled na Obr.2 vzbuzuje i bez ohledu na to některé pochybnosti. Abychom je mohli formulovat, dívejme se na něj jako na 3 krát 5 matici ![]() a očíslujme obrázky v souladu s tím. Proč je chování modelů v prvním sloupci kvalitativně stejné bez ohledu na hodnotu
a očíslujme obrázky v souladu s tím. Proč je chování modelů v prvním sloupci kvalitativně stejné bez ohledu na hodnotu ![]() ?
?
Proč je kvalitativně stejné také chování modelů ![]() ;
; ![]() ;
;![]() ? Co znamená přerušovaná horizontální čára v
? Co znamená přerušovaná horizontální čára v ![]() a proč chybí modely s grafy pod touto čarou? A hlavně: Můžeme chování modelů objasnit i bez řešení rovnic (které by si ve složitějích případech vyžadovalo znalost eliptických funkcí)? Odpověď na tyto otázky bude hlavní částí našeho článku.
a proč chybí modely s grafy pod touto čarou? A hlavně: Můžeme chování modelů objasnit i bez řešení rovnic (které by si ve složitějích případech vyžadovalo znalost eliptických funkcí)? Odpověď na tyto otázky bude hlavní částí našeho článku.
Grafické znázornění a interpretace
Začněme případem ![]() . Znázorněme graficky závislost veličiny
. Znázorněme graficky závislost veličiny ![]() z rovnice (5) na škálovém faktoru
z rovnice (5) na škálovém faktoru ![]() (Obr.3). Stav modelu v určitém čase je určen bodem na vodorovné ose, člen
(Obr.3). Stav modelu v určitém čase je určen bodem na vodorovné ose, člen ![]() , který je nutně nezáporný, je podle rovnice (9) dán vzdáleností od křivky
, který je nutně nezáporný, je podle rovnice (9) dán vzdáleností od křivky ![]() k této ose. Model proto může být pouze ve stavu, který je v grafu umístěn nad křivkou. Dostáváme tak tři typy chování, přičemž jeden z nich
k této ose. Model proto může být pouze ve stavu, který je v grafu umístěn nad křivkou. Dostáváme tak tři typy chování, přičemž jeden z nich ![]() je hraniční případ mezi zbývajícími dvěma.
je hraniční případ mezi zbývajícími dvěma.
Poznamenejme, že tohoto případu si zakladatel vývojové kosmologie Fridman explicitně nepovšiml a upozornili na něj a Einstein s de Sitterem, podle nich se nazývá Einsteinův de Sitterův vesmír. Je třeba jej rozlišovat od statického vesmíru Einsteinova i od stacionárního vesmíru de Sitterova, o nich se ještě zmíníme. Vývoj modelů vždy začíná ze singularity. Pro ![]() se derivace škálového faktoru podle času blíží asymptoticky k určité hodnotě, která je v hraničním případě
se derivace škálového faktoru podle času blíží asymptoticky k určité hodnotě, která je v hraničním případě ![]() nulová. Pro
nulová. Pro ![]() se rozpínání zastaví v průsečíku křivky s osou a je vystřídáno smršťováním končícím v singularitě.
se rozpínání zastaví v průsečíku křivky s osou a je vystřídáno smršťováním končícím v singularitě.

Obr.3
Obr. 4
Obr.5
Toto chování lze fyzikálně vyložit jako střetnutí mezi newtonovskou gravitací a setrvačností. Gravitace zpomaluje rozpínání, ale sama je jím zeslabována, v závislosti na počátečních podmínkách buď zvítězí a rozpínání bude nahrazeno smršťováním anebo bude schopna rozpínání pouze po nekonečnou dobu zpomalovat. Toho si Einstein, který zavedl tento model v rámci obecné teorie relativity, nebyl vědom.
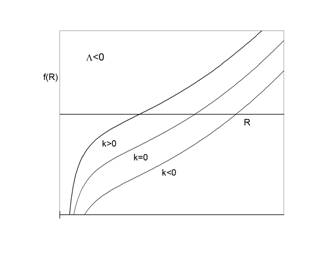
Nyní přejděme k případu ![]() (Obr. 4). Do hry vstupuje další faktor, kosmologický člen, který má na rozdíl od newtonovské gravitace tendenci setrvačné rozpínání urychlovat. Leží-li graf celý pod osou, pro
(Obr. 4). Do hry vstupuje další faktor, kosmologický člen, který má na rozdíl od newtonovské gravitace tendenci setrvačné rozpínání urychlovat. Leží-li graf celý pod osou, pro ![]() a ještě i pro
a ještě i pro ![]() , dochází ve vývoji vesmíru k zaváhání, zpomalování expanze vesmíru se po nějaké době zastaví a vesmír se začíná opět urychlovat kosmologický člen se ujme dominance nad newtonovskou gravitací.
, dochází ve vývoji vesmíru k zaváhání, zpomalování expanze vesmíru se po nějaké době zastaví a vesmír se začíná opět urychlovat kosmologický člen se ujme dominance nad newtonovskou gravitací.
Při jisté kritické hodnotě ![]() , která závisí na konstantách
, která závisí na konstantách ![]() a C může být vesmír statický (dotykový bod křivky a vodorovné osy).
a C může být vesmír statický (dotykový bod křivky a vodorovné osy).
Z Obr. 4 je ovšem zřejmé, že tento model představuje nestabilní stav, který nemůže odpovídat realitě. Jak vidíme z ![]() , může se (z čistě formálního hlediska) vesmír smršťovat z nekonečna a ještě před dosažením einsteinovského stavu se zastavit a začít se rozpínat. K podobnému obratu, který na Obr. 2 chybí, může dojít i při vývoji od singularity vesmír se jetě před dosažením vrcholu valu zastaví a začne se opět smršťovat.
, může se (z čistě formálního hlediska) vesmír smršťovat z nekonečna a ještě před dosažením einsteinovského stavu se zastavit a začít se rozpínat. K podobnému obratu, který na Obr. 2 chybí, může dojít i při vývoji od singularity vesmír se jetě před dosažením vrcholu valu zastaví a začne se opět smršťovat.
Z ![]() vidíme, e vesmír se také můe einsteinovskému stavu statičnosti asymptoticky blížit. Na Obr.2 je opět opomenuta možnost, že se tak může dít nejen z nekonečna, ale i ze singularity. Poznamenejme, že podle současných empirických dat odpovídá reálný vesmír (v mezích pozorovacích chyb) hodnotě
vidíme, e vesmír se také můe einsteinovskému stavu statičnosti asymptoticky blížit. Na Obr.2 je opět opomenuta možnost, že se tak může dít nejen z nekonečna, ale i ze singularity. Poznamenejme, že podle současných empirických dat odpovídá reálný vesmír (v mezích pozorovacích chyb) hodnotě ![]() (tedy z hlediska obecné teorie relativity nulové křivosti prostoru). Proč tomu tak je, zůstává velkou otevřenou otázkou. V současné době se vesmír rozpíná zrychleně a na Obr.2 tedy odpovídá políčku
(tedy z hlediska obecné teorie relativity nulové křivosti prostoru). Proč tomu tak je, zůstává velkou otevřenou otázkou. V současné době se vesmír rozpíná zrychleně a na Obr.2 tedy odpovídá políčku ![]() .
.
V případě ![]() (Obr.5) kosmologický člen podporuje newtonovskou gravitaci a rozpínání se, proto v kadém případě zastaví a je následováno smršťováním.
(Obr.5) kosmologický člen podporuje newtonovskou gravitaci a rozpínání se, proto v kadém případě zastaví a je následováno smršťováním.
Je moné uvažovat jetě také o případu, kdy ![]() (vesmír bez hmotné náplně). Zajímavý je zejména případ de Sitterova vesmíru, kdy
(vesmír bez hmotné náplně). Zajímavý je zejména případ de Sitterova vesmíru, kdy ![]() a
a ![]() . To je de Sitterův stacionární vesmír, v něm je Hubbleova konstanta skutečnou konstantou. Vesmír se tedy rozpíná zrychleně, ale vypadá přitom stále stejně. K tomuto stavu se možná (je-li kosmologická konstanta skutečně konstantou v libovolném časovém měřítku a nedojde-li k nepředvídaným fázovým přechodům vesmírné hmoty) skutečný vesmír bude asymptoticky blížit. Další přinejmenším z pedagogického hlediska zajímavý případ odpovídá hodnotám
. To je de Sitterův stacionární vesmír, v něm je Hubbleova konstanta skutečnou konstantou. Vesmír se tedy rozpíná zrychleně, ale vypadá přitom stále stejně. K tomuto stavu se možná (je-li kosmologická konstanta skutečně konstantou v libovolném časovém měřítku a nedojde-li k nepředvídaným fázovým přechodům vesmírné hmoty) skutečný vesmír bude asymptoticky blížit. Další přinejmenším z pedagogického hlediska zajímavý případ odpovídá hodnotám ![]() a
a ![]() . V tomto případě se vesmír, fakticky vztažná soustava v prázdném eukleidovském prostoru realizovaná částicemi o zanedbatelné hustotě, setrvačně rozpíná.
. V tomto případě se vesmír, fakticky vztažná soustava v prázdném eukleidovském prostoru realizovaná částicemi o zanedbatelné hustotě, setrvačně rozpíná.
Diskuse
Ukázali jsme, že chování kosmologických modelů odpovídajících homogenitě, isotropii a nulovému tlaku, je možno vysvětlit prostředky bez použití obecné teorie relativity. Kromě rozboru rovnice (9) a jejího grafického znázornění, což je možno provést prostředky středoškolské matematiky, potřebujeme pro odvození této rovnice newtonovskou fyziku. Je věcí diskuse, zda newtonovská kosmologie neodvádí pozornost od faktu, že co se týče gravitace, je newtonovská fyzika překonána obecnou teorií relativity a nemůže řešit složitějí kosmologické problémy. Domníváme se však, že stejně jako newtonovská fyzika, je i obecná teorie relativity jen přiblížením k realitě a není proto nepřípustné nahradit složitějí obraz jednodušším tam, kde vede k přijatelnému vysvětlení.