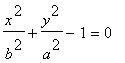
Předpokládejme, že máme dány parametry a,b,c (a>0,b>0,c>b) a máme dánu elipsu se středem v počátku kartézské soustavy souřadnic a poloosami a, resp. b na osách y, resp. x a parabolu protínající osu y s vrcholem v bodě [c,0]. Pak dostáváme implicitní rovnice elipsy a paraboly tvaru:
(1) 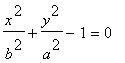
(2) ![]()
Budiž úkolem určit hodnoty neznámých x,y,p, abychom dostali hladké napojení těchto křivek. Z rovnic (1) a (2) jsme schopni v závislosti na parametru p paraboly určit jejich průsečíky. Přidáme další podmínku (3) - rovnost směrnic tečen k oběma křivám v témž bodě (průsečíku [x,y]):
(3) 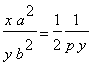
Máme celkem 3 nelineární rovnice pro 3 neznámé, které budeme řešit v oboru reálných čísel. Bez újmy na obecnosti lze předpokládat, že p>0. Jinak by se elipsa a parabola vůbec reálně neprotínaly. Uvážíme-li souměrnost, podle osy x, pak je-li hledaným průsečíkem bod o souřadnicích [x,y], pak je průsečíkem i bod [x,-y], tedy stačí řešit soustavu pro y>0. Uvážme části obou křivek ležící pouze v prvním a druhém kvadrantu a na elipse (jejichž y-ová souřadnice je větší než 0 na menší než a). Směrnice tečny k parabole se tak nedostane nikdy do kladných hodnot. Směrnice tečny k elipse se tak nedostane nikdy do kladných hodnot pouze v prvním kvadrantu, zatímco v druhém nikdy do záporných. Má tedy smysl hledat průsečík pouze v prvním kvadrantu, tedy pro x>0. Zároveň hledaný bod leží na uvažované parabole, tedy x<c. Navíc v prvním kvadrantu s rostoucími hodnotami x-ové souřadnice klesají hodnoty směrnice tečny k elipse a rostou hodnoty směrnice tečny k parabole. Což ale neznamená nic jiného, než, že pokud existuje hladké napojení obou křivek, tak jak jej hledáme, pak je jediné. Začněme tedy s řešením soustavy.
Z rovnice (2) dostáváme:
![]()
Dosazením do rovnice (1) pak:

Uvažujeme však pouze y>0, tedy:

Dosadíme za y do (2) a dostáváme:

Spočtený bod musí ležet na elipse, tedy dosadíme za x,y do (1) a vypočítáme p:

Kontrolou zjistíme, že druhé řešení zadaným podmínkám nevyhovuje, tedy:

Zpětným dosazením do vztahů pro x,y dostáváme:


Po úpravě:
![]()
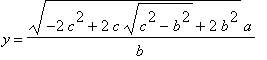
Toto řešení je za daných podmínek vždy korektní a právě jedno, nezapomeňme však na druhý průsečík, resp. bod dotyku obou křivek (oba jsou souměrné podle osy x).
Například pro hodnoty a=3, b=4, c=5 je hodnota parametru p=4/9:
