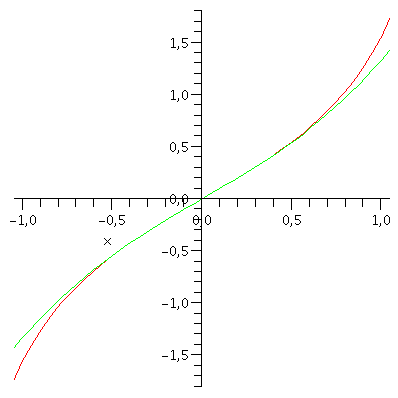Diferenciál, Taylorův polynom
Příklad 1
Pomocí diferenciálu vypočtěte přibližně 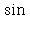 29 stupňů. Namalujte graf, na kterém bude původni funkce a funkce použitá k aproximaci.
29 stupňů. Namalujte graf, na kterém bude původni funkce a funkce použitá k aproximaci.
![(Typesetting:-mprintslash)([f := proc (x) options operator, arrow; sin(x) end proc], [proc (x) options operator, arrow; sin(x) end proc])](images/taylor_2.gif)
![(Typesetting:-mprintslash)([x0 := 1/6*Pi], [1/6*Pi])](images/taylor_3.gif)
![(Typesetting:-mprintslash)([xx := 29/180*Pi], [29/180*Pi])](images/taylor_4.gif)
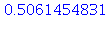
![(Typesetting:-mprintslash)([h := -1/180*Pi], [-1/180*Pi])](images/taylor_6.gif)
![(Typesetting:-mprintslash)([dx := cos], [cos])](images/taylor_7.gif)
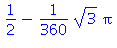


| > |
df:=f(x0)+dx(x0)*(x-x0); |
![(Typesetting:-mprintslash)([df := 1/2+1/2*3^(1/2)*(x-1/6*Pi)], [1/2+1/2*3^(1/2)*(x-1/6*Pi)])](images/taylor_11.gif)
| > |
plot([f(x), df], x=0..Pi/2); |
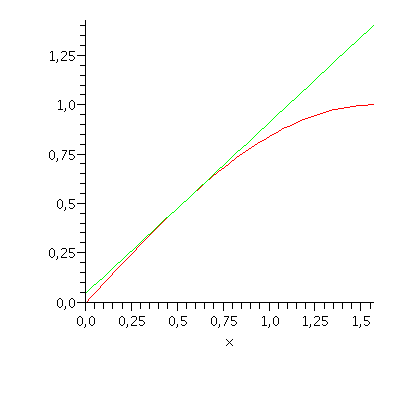
Příklad 2
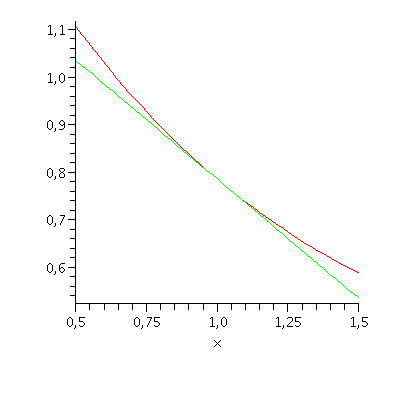
Vypočtěte přibližně arccotg 1,02. Stejně jako v předcházejícím příkladě namalujte grafy obou funkcí.
![(Typesetting:-mprintslash)([f := proc (x) options operator, arrow; arccot(x) end proc], [proc (x) options operator, arrow; arccot(x) end proc])](images/taylor_13.gif)
![(Typesetting:-mprintslash)([df := proc (x) options operator, arrow; -1/(1+x^2) end proc], [proc (x) options operator, arrow; -1/(1+x^2) end proc])](images/taylor_14.gif)
![(Typesetting:-mprintslash)([x0 := 1], [1])](images/taylor_15.gif)
![(Typesetting:-mprintslash)([h := 0.2e-1], [0.2e-1])](images/taylor_16.gif)
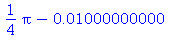
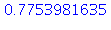
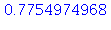
| > |
plot([f(x), f(x0)+df(x0)*(x-x0)], x=0.5..1.5); |
Příklad 3
Určete Taylorův polynom stupně 4 pro funkci 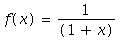 a
a ![x[0]](images/taylor_22.gif) =0. Namalujte graf zadané funkce a Taylorova polynomu.
=0. Namalujte graf zadané funkce a Taylorova polynomu.
Dále vypočtěte chybu, které se dopustíte, pokud použijete ](images/taylor_23.gif) pro výpočet funkční hodnoty
pro výpočet funkční hodnoty 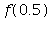 . Namalujte graf chyby pro
. Namalujte graf chyby pro  〉.
〉.
![(Typesetting:-mprintslash)([f := proc (x) options operator, arrow; 1/(1+x) end proc], [proc (x) options operator, arrow; 1/(1+x) end proc])](images/taylor_26.gif)
![(Typesetting:-mprintslash)([x0 := 0], [0])](images/taylor_27.gif)
![(Typesetting:-mprintslash)([c0 := 1], [1])](images/taylor_28.gif)
| > |
c1:=D(f)(x0)*(x-x0)/1!; |
![(Typesetting:-mprintslash)([c1 := -x], [-x])](images/taylor_29.gif)
| > |
c2:=D[1,1](f)(x0)*(x-x0)^2/2!; |
![(Typesetting:-mprintslash)([c2 := x^2], [x^2])](images/taylor_30.gif)
| > |
c3:=D[1,1,1](f)(x0)*(x-x0)^3/3!; |
![(Typesetting:-mprintslash)([c3 := -x^3], [-x^3])](images/taylor_31.gif)
| > |
c4:=D[1,1,1,1](f)(x0)*(x-x0)^4/4!; |
![(Typesetting:-mprintslash)([c4 := x^4], [x^4])](images/taylor_32.gif)
| > |
c4:=(D@@4)(f)(x0)*(x-x0)^4/4!; |
![(Typesetting:-mprintslash)([c4 := x^4], [x^4])](images/taylor_33.gif)
| > |
tn:=(n, x0)->(D@@n)(f)(x0)*(x-x0)^n/n!; |
![(Typesetting:-mprintslash)([tn := proc (n, x0) options operator, arrow; ((`@@`(D, n))(f))(x0)*(x-x0)^n/factorial(n) end proc], [proc (n, x0) options operator, arrow; ((`@@`(D, n))(f))(x0)*(x-x0)^n/fac...](images/taylor_34.gif)
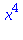
![(Typesetting:-mprintslash)([T4 := 1-x+x^2-x^3+x^4], [1-x+x^2-x^3+x^4])](images/taylor_36.gif)
| > |
plot([f(x), T4], x=-1..1, y=0..100, color=[red, blue]); |
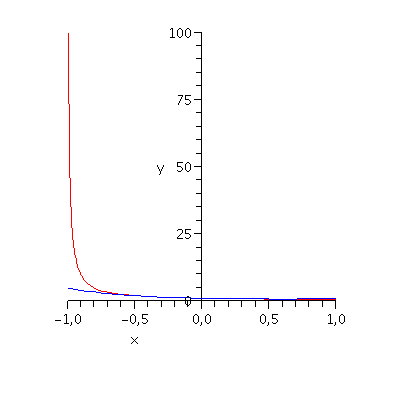
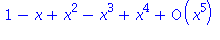

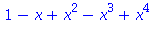
![proc () local f, k, v, m, n, s, t, w; option `Copyright (c) 1991 by the University of Waterloo. All rights reserved.`; f := args[1]; v := args[2]; if type(v, set) then v := [op(v)] elif not type(v, li...](images/taylor_41.gif)
| > |
T:=unapply(mtaylor(f(x), x=x0, 5),x); |
![(Typesetting:-mprintslash)([T := proc (x) options operator, arrow; 1-x+x^2-x^3+x^4 end proc], [proc (x) options operator, arrow; 1-x+x^2-x^3+x^4 end proc])](images/taylor_42.gif)
| > |
evalf(abs(f(0.5)-T(0.5))); |
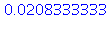
| > |
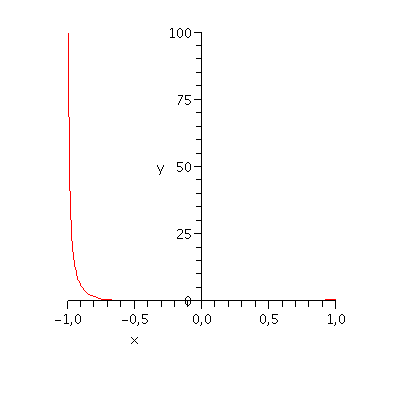
plot(abs(f(x)-T(x)), x=-1..1, y=0..100); |
Příklad 4
Napište Taylorův polynom 3. stupně v bodě ![x[0]](images/taylor_45.gif) =0 funkce
=0 funkce 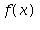 =tg
=tg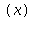 .
.
![(Typesetting:-mprintslash)([f := proc (x) options operator, arrow; tan(x) end proc], [proc (x) options operator, arrow; tan(x) end proc])](images/taylor_48.gif)
![(Typesetting:-mprintslash)([derivace1 := proc (x) options operator, arrow; 1+tan(x)^2 end proc], [proc (x) options operator, arrow; 1+tan(x)^2 end proc])](images/taylor_49.gif)
![(Typesetting:-mprintslash)([derivace2 := proc (x) options operator, arrow; 2*tan(x)*(1+tan(x)^2) end proc], [proc (x) options operator, arrow; 2*tan(x)*(1+tan(x)^2) end proc])](images/taylor_50.gif)
![(Typesetting:-mprintslash)([derivace3 := proc (x) options operator, arrow; 2*(1+tan(x)^2)^2+4*tan(x)^2*(1+tan(x)^2) end proc], [proc (x) options operator, arrow; 2*(1+tan(x)^2)^2+4*tan(x)^2*(1+tan(x)^...](images/taylor_51.gif)
| > |
TayloruvPolynom[3]:=f(0)+derivace1(0)*x+derivace2(0)*x^2/(2!)+derivace3(0)*x^3/(3!); |
![(Typesetting:-mprintslash)([TayloruvPolynom[3] := x+1/3*x^3], [x+1/3*x^3])](images/taylor_52.gif)
| > |
TaylorPol:=(f,x0,n)->sum((D@@i)(f)(x0)/i!*(x-x0)^i,i=0..n); |
![(Typesetting:-mprintslash)([TaylorPol := proc (f, x0, n) options operator, arrow; sum(((`@@`(D, i))(f))(x0)*(x-x0)^i/factorial(i), i = 0 .. n) end proc], [proc (f, x0, n) options operator, arrow; sum(...](images/taylor_53.gif)
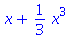
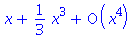
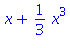
| > |
plot([f(x), TayloruvPolynom[3]], x=-Pi/3..Pi/3); |
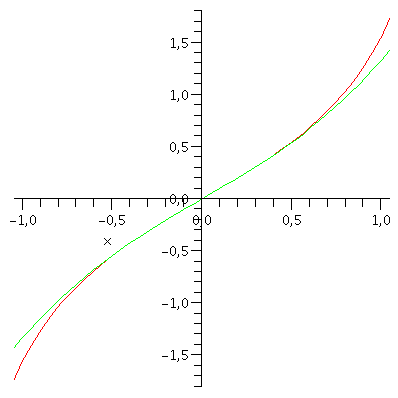
| > |
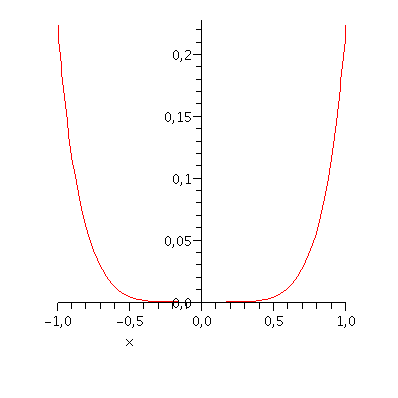
plot(abs(f(x)-TaylorPol(f,0,3)), x=-1..1); |
![]() 29 stupňů. Namalujte graf, na kterém bude původni funkce a funkce použitá k aproximaci.
29 stupňů. Namalujte graf, na kterém bude původni funkce a funkce použitá k aproximaci. ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()


![(Typesetting:-mprintslash)([tn := proc (n, x0) options operator, arrow; ((`@@`(D, n))(f))(x0)*(x-x0)^n/factorial(n) end proc], [proc (n, x0) options operator, arrow; ((`@@`(D, n))(f))(x0)*(x-x0)^n/fac...](images/taylor_34.gif)


![(Typesetting:-mprintslash)([derivace3 := proc (x) options operator, arrow; 2*(1+tan(x)^2)^2+4*tan(x)^2*(1+tan(x)^2) end proc], [proc (x) options operator, arrow; 2*(1+tan(x)^2)^2+4*tan(x)^2*(1+tan(x)^...](images/taylor_51.gif)
![(Typesetting:-mprintslash)([TaylorPol := proc (f, x0, n) options operator, arrow; sum(((`@@`(D, i))(f))(x0)*(x-x0)^i/factorial(i), i = 0 .. n) end proc], [proc (f, x0, n) options operator, arrow; sum(...](images/taylor_53.gif)