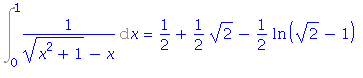Příklad 1
| > | i1:=Int((x^2+1)*ln(x), x=1..2); |
![(Typesetting:-mprintslash)([i1 := Int((x^2+1)*ln(x), x = 1 .. 2)], [Int((x^2+1)*ln(x), x = 1 .. 2)])](imagesurcint/urcint_1.gif)
| > | i1=intparts(i1, ln(x)); |
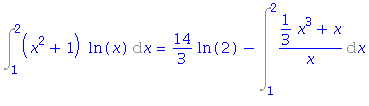
| > | i1=value(lhs(%)); |
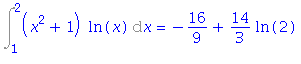
Výpočet určitého integralu
Metoda per partes pro určitý integrál
| > | with(student): |
Příklad 1
| > | i1:=Int((x^2+1)*ln(x), x=1..2); |
![(Typesetting:-mprintslash)([i1 := Int((x^2+1)*ln(x), x = 1 .. 2)], [Int((x^2+1)*ln(x), x = 1 .. 2)])](imagesurcint/urcint_1.gif)
| > | i1=intparts(i1, ln(x)); |
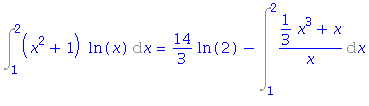
| > | i1=value(lhs(%)); |
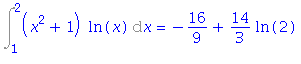
Příklad 2
| > | i2:=Int(x^2*cos(x), x=0..Pi); |
![(Typesetting:-mprintslash)([i2 := Int(x^2*cos(x), x = 0 .. Pi)], [Int(x^2*cos(x), x = 0 .. Pi)])](imagesurcint/urcint_4.gif)
| > | i2=intparts(i2, x^2); |
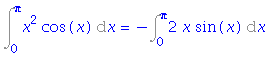
| > | i2=intparts(rhs(%), 2*x); |
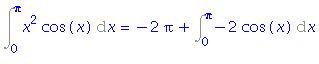
| > | i2=value(rhs(%)); |
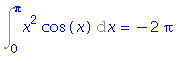
Příklad 3
| > | i3:=Int(exp(x)*cos(x), x=0..Pi); |
![(Typesetting:-mprintslash)([i3 := Int(exp(x)*cos(x), x = 0 .. Pi)], [Int(exp(x)*cos(x), x = 0 .. Pi)])](imagesurcint/urcint_8.gif)
| > | intparts(i3, cos(x)); |
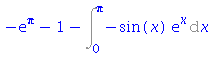
| > | i3=intparts(%, sin(x)); |
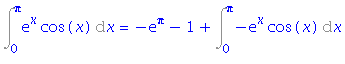
| > | simplify(%); |
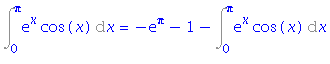
| > | isolate(%,i3); |
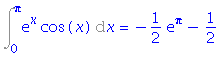
Substituční metoda pro určitý integrál
Příklad 4
| > | i4:=Int(x*(x^2-1)^3, x=0..1); |
![(Typesetting:-mprintslash)([i4 := Int(x*(x^2-1)^3, x = 0 .. 1)], [Int(x*(x^2-1)^3, x = 0 .. 1)])](imagesurcint/urcint_13.gif)
| > | i4=changevar(x^2-1=t, i4, t); |
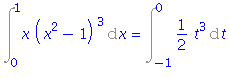
| > | i4=value(rhs(%)); |
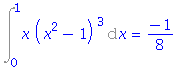
Příklad 5
| > | i5:=Int(exp(sin(x))*cos(x), x=Pi..2*Pi); |
![(Typesetting:-mprintslash)([i5 := Int(exp(sin(x))*cos(x), x = Pi .. 2*Pi)], [Int(exp(sin(x))*cos(x), x = Pi .. 2*Pi)])](imagesurcint/urcint_16.gif)
| > | i5=changevar(sin(x)=t, i5, t); |
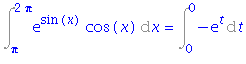
| > | i5=value(rhs(%)); |
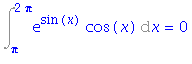
Příklad 6
| > | i6:=Int(sin(x)*cos(x)^2/(1+cos(x)^3)^(1/4), x=0..Pi/2); |
![(Typesetting:-mprintslash)([i6 := Int(sin(x)*cos(x)^2/(1+cos(x)^3)^(1/4), x = 0 .. 1/2*Pi)], [Int(sin(x)*cos(x)^2/(1+cos(x)^3)^(1/4), x = 0 .. 1/2*Pi)])](imagesurcint/urcint_19.gif)
| > | mezi:=i6=changevar(1+cos(x)^3=u, i6, u); |
![(Typesetting:-mprintslash)([mezi := Int(sin(x)*cos(x)^2/(1+cos(x)^3)^(1/4), x = 0 .. 1/2*Pi) = Int(1/3/u^(1/4), u = 1 .. 2)], [Int(sin(x)*cos(x)^2/(1+cos(x)^3)^(1/4), x = 0 .. 1/2*Pi) = Int(1/3/u^(1/4...](imagesurcint/urcint_20.gif)
"Ruční" kontrola nových mezí:
| > | dolni:=1+cos(0); |
![]()
| > | horni:=1+cos(Pi/2); |
![]()
| > | du:=diff(1+cos(x)^3,x); |
![]()
| > | i6=value(rhs(mezi)); |
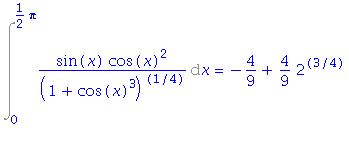
Příklad 7
| > | i7:=Int((sqrt(x)-1)/(sqrt(x)+1), x=1..4); |
![(Typesetting:-mprintslash)([i7 := Int((x^(1/2)-1)/(x^(1/2)+1), x = 1 .. 4)], [Int((x^(1/2)-1)/(x^(1/2)+1), x = 1 .. 4)])](imagesurcint/urcint_25.gif)
| > | assume(u>0); |
| > | i7=simplify(changevar(x=u^2, i7, u)); |
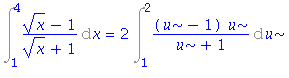
| > | i7=simplify(value(rhs(%))); |
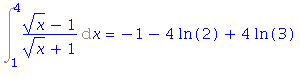
Příklad 8
| > | i8:=Int(1/(sqrt(x^2+1)-x), x=0..1); |
![(Typesetting:-mprintslash)([i8 := Int(1/((x^2+1)^(1/2)-x), x = 0 .. 1)], [Int(1/((x^2+1)^(1/2)-x), x = 0 .. 1)])](imagesurcint/urcint_28.gif)
| > | assume(t>0); |
| > | i8=simplify(changevar(sqrt(x^2+1)-x=t, i8, t)); |
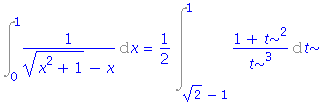
| > | i8=value(rhs(%)); |
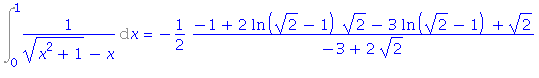
| > | i8=expand(rationalize((rhs(%)))); |