obsah.mw
Načtení balíků a procedur
| > |
with(plots):with(plottools): |
Warning, the name changecoords has been redefined
Warning, the assigned name arrow now has a global binding
Příklad 1
Určete obsah množiny ohraničené grafy funkcí f: y=- a g: y=
a g: y=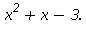
![(Typesetting:-mprintslash)([g := proc (x) options operator, arrow; x^2+x-3 end proc], [proc (x) options operator, arrow; x^2+x-3 end proc])](imagesobsah/obsah_3.gif)
![(Typesetting:-mprintslash)([f := proc (x) options operator, arrow; -x^2-2*x+2 end proc], [proc (x) options operator, arrow; -x^2-2*x+2 end proc])](imagesobsah/obsah_4.gif)

| > |
plot({f(x), g(x)}, x=-3..2, scaling=constrained); |

| > |
v:=plot({f(x), g(x)}, x=-3..2, scaling=constrained): |
| > |
pic:=shadein(f,g,[-5/2,1], gray): |

| > |
m:=Int(f(x)-g(x), x=-5/2..1); |
![(Typesetting:-mprintslash)([m := Int(-2*x^2-3*x+5, x = (-5)/2 .. 1)], [Int(-2*x^2-3*x+5, x = (-5)/2 .. 1)])](imagesobsah/obsah_8.gif)

Příklad 2
Vypočtěte obsah kruhu o poloměru r>0.
![(Typesetting:-mprintslash)([f := proc (x) options operator, arrow; sqrt(r^2-x^2) end proc], [proc (x) options operator, arrow; sqrt(r^2-x^2) end proc])](imagesobsah/obsah_10.gif)
![(Typesetting:-mprintslash)([g := proc (x) options operator, arrow; -sqrt(r^2-x^2) end proc], [proc (x) options operator, arrow; -sqrt(r^2-x^2) end proc])](imagesobsah/obsah_11.gif)
| > |
m:=Int(f(x)-g(x), x=-r..r); |
![(Typesetting:-mprintslash)([m := Int(2*(r^2-x^2)^(1/2), x = -r .. r)], [Int(2*(r^2-x^2)^(1/2), x = -r .. r)])](imagesobsah/obsah_12.gif)

Příklad 3
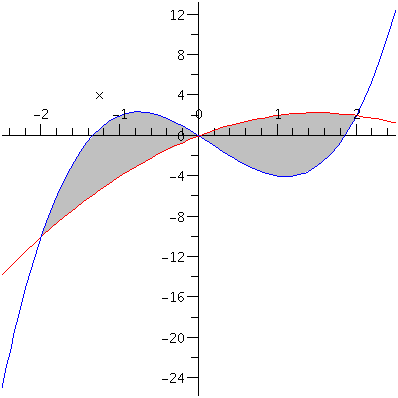
Určete obsah množiny ohraničené grafy funkcí f: y=-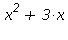 a g: 2*
a g: 2*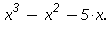
![(Typesetting:-mprintslash)([f := proc (x) options operator, arrow; -x^2+3*x end proc], [proc (x) options operator, arrow; -x^2+3*x end proc])](imagesobsah/obsah_16.gif)
![(Typesetting:-mprintslash)([g := proc (x) options operator, arrow; 2*x^3-x^2-5*x end proc], [proc (x) options operator, arrow; 2*x^3-x^2-5*x end proc])](imagesobsah/obsah_17.gif)

| > |
plot({f(x), g(x)}, x=-2.5..2.5); |
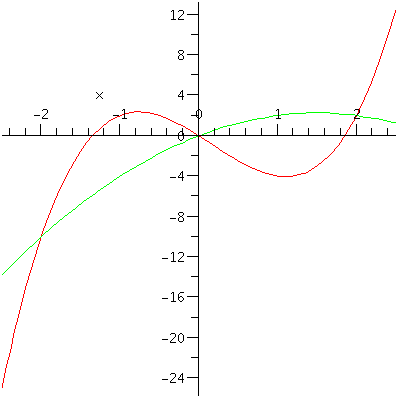
| > |
pic:=shadein(f,g,[-2,2], gray): |
| > |
v:=plot([f(x), g(x)], x=-2.5..2.5,color=[red, blue]): |
| > |
m:=Int(g(x)-f(x), x=-2..0)+Int(f(x)-g(x), x=0..2); |
![(Typesetting:-mprintslash)([m := Int(2*x^3-8*x, x = -2 .. 0)+Int(8*x-2*x^3, x = 0 .. 2)], [Int(2*x^3-8*x, x = -2 .. 0)+Int(8*x-2*x^3, x = 0 .. 2)])](imagesobsah/obsah_21.gif)

Příklad 4
Určete obsah množiny ohraničené křivkou danou parametricky  a osou x.
a osou x.
| > |
plot([t-sin(t), 1-cos(t), t=0..2*Pi], scaling=constrained, filled=true, color=gray); |

| > |
m:=Int((1-cos(t))*abs(Diff(t-sin(t), t)), t=0..2*Pi); |
![(Typesetting:-mprintslash)([m := Int((1-cos(t))*abs(Diff(t-sin(t), t)), t = 0 .. 2*Pi)], [Int((1-cos(t))*abs(Diff(t-sin(t), t)), t = 0 .. 2*Pi)])](imagesobsah/obsah_25.gif)
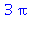
Příklad 5
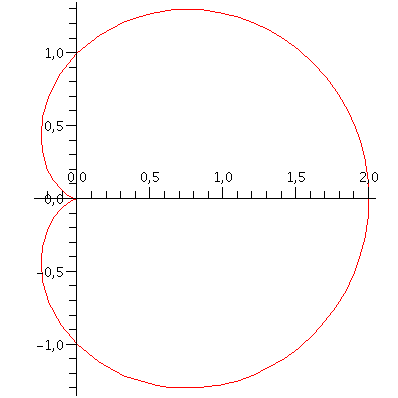
Určete obsah množiny omezené kardioidou ϱ=1+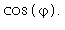
| > |
polarplot(1+cos(phi), phi=0..2*Pi, scaling=constrained); |
| > |
m:=Int((1+cos(phi))^2, phi=0..2*Pi); |
![(Typesetting:-mprintslash)([m := Int((1+cos(phi))^2, phi = 0 .. 2*Pi)], [Int((1+cos(phi))^2, phi = 0 .. 2*Pi)])](imagesobsah/obsah_29.gif)

![]() a g: y=
a g: y=![]()
![]()
![]()
![]()


![(Typesetting:-mprintslash)([m := Int(-2*x^2-3*x+5, x = (-5)/2 .. 1)], [Int(-2*x^2-3*x+5, x = (-5)/2 .. 1)])](imagesobsah/obsah_8.gif)
![]()
![(Typesetting:-mprintslash)([m := Int(2*(r^2-x^2)^(1/2), x = -r .. r)], [Int(2*(r^2-x^2)^(1/2), x = -r .. r)])](imagesobsah/obsah_12.gif)


![(Typesetting:-mprintslash)([m := Int(2*x^3-8*x, x = -2 .. 0)+Int(8*x-2*x^3, x = 0 .. 2)], [Int(2*x^3-8*x, x = -2 .. 0)+Int(8*x-2*x^3, x = 0 .. 2)])](imagesobsah/obsah_21.gif)

![(Typesetting:-mprintslash)([m := Int((1-cos(t))*abs(Diff(t-sin(t), t)), t = 0 .. 2*Pi)], [Int((1-cos(t))*abs(Diff(t-sin(t), t)), t = 0 .. 2*Pi)])](imagesobsah/obsah_25.gif)

![(Typesetting:-mprintslash)([m := Int((1+cos(phi))^2, phi = 0 .. 2*Pi)], [Int((1+cos(phi))^2, phi = 0 .. 2*Pi)])](imagesobsah/obsah_29.gif)