perpartes.mw

Základní integrační metody - metoda per partes 

K naznačení postupu výpočtu metodou per partes použijeme proceduru intparts z balíku student. 

> with(student):
 

> Int(u(x)*Diff(v(x), x), x)=intparts(Int(u(x)*Diff(v(x),x),x), u(x));
 

(Typesetting:-mprintslash)([Int(u(x)*(Diff(v(x), x)), x) = u(x)*v(x)-Int((diff(u(x), x))*v(x), x)], [Int(u(x)*(Diff(v(x), x)), x) = u(x)*v(x)-Int((diff(u(x), x))*v(x), x)]) 

Řešte následující integrály za pomoci programu Maple. 

> i1:=Int(x*cos(x), x);
 

(Typesetting:-mprintslash)([i1 := Int(x*cos(x), x)], [Int(x*cos(x), x)]) 

> i1=intparts(Int(x*cos(x), x), x);
 

Int(x*cos(x), x) = x*sin(x)-Int(sin(x), x) 

> i1=value(rhs(%));
 

Int(x*cos(x), x) = x*sin(x)+cos(x) 

Kontrola výsledku přímým výpočtem: 

> i1=value(i1);
 

Int(x*cos(x), x) = x*sin(x)+cos(x) 

> i2:=Int((x^2+1)*exp(-x), x);
 

(Typesetting:-mprintslash)([i2 := Int((x^2+1)*exp(-x), x)], [Int((x^2+1)*exp(-x), x)]) 

> i2=intparts(i2, x^2+1);
 

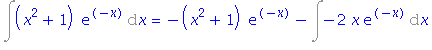
Int((x^2+1)*exp(-x), x) = -(x^2+1)*exp(-x)-Int(-2*x*exp(-x), x) 

> simplify(%);
 

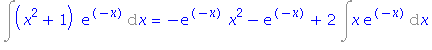
Int((x^2+1)*exp(-x), x) = -exp(-x)*x^2-exp(-x)+2*Int(x*exp(-x), x) 

Použijeme metodu per partes ještě jednou 

> i2=intparts(rhs(%), x);
 

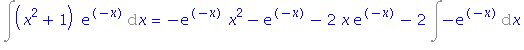
Int((x^2+1)*exp(-x), x) = -exp(-x)*x^2-exp(-x)-2*x*exp(-x)-2*Int(-exp(-x), x) 

> i2=simplify(value(rhs(%)));
 

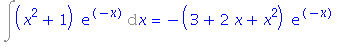
Int((x^2+1)*exp(-x), x) = -(3+2*x+x^2)*exp(-x) 

> i2=value(i2);
 

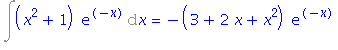
Int((x^2+1)*exp(-x), x) = -(3+2*x+x^2)*exp(-x) 

> i3:=Int(arccot(x), x);
 

(Typesetting:-mprintslash)([i3 := Int(arccot(x), x)], [Int(arccot(x), x)]) 

> i3=intparts(i3, arccot(x));
 

Int(arccot(x), x) = arccot(x)*x-Int(-x/(x^2+1), x) 

> i3=value(rhs(%));
 

Int(arccot(x), x) = arccot(x)*x+1/2*ln(x^2+1) 

> i4:=Int(exp(x)*sin(x), x);
 

(Typesetting:-mprintslash)([i4 := Int(exp(x)*sin(x), x)], [Int(exp(x)*sin(x), x)]) 

> i4=intparts(i4, exp(x));
 

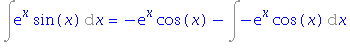
Int(exp(x)*sin(x), x) = -exp(x)*cos(x)-Int(-exp(x)*cos(x), x) 

Použijeme znovu metodu per partes a pravou stranu rovnice zjednodušíme. 

> i4=simplify(intparts(rhs(%), exp(x)));
 

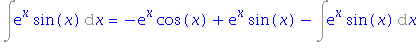
Int(exp(x)*sin(x), x) = -exp(x)*cos(x)+exp(x)*sin(x)-Int(exp(x)*sin(x), x) 

Ze ziskané rovnice již snadno vypočítáme, že 

> simplify(isolate(%, i4));
 

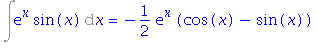
Int(exp(x)*sin(x), x) = -1/2*exp(x)*(cos(x)-sin(x)) 

>