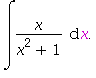
Substituční metoda 

Pro integraci substitucí existuje v balíku student příkaz changevar. 

> with(student):
 

Vypočtěte neurčitý integrál  

Použijeme substituci  

> e1:=Int(x/(x^2+1), x);
 

(Typesetting:-mprintslash)([e1 := Int(x/(x^2+1), x)], [Int(x/(x^2+1), x)]) 

> g:=changevar(x^2+1=t, e1, t);
 

(Typesetting:-mprintslash)([g := Int(1/2/t, t)], [Int(1/2/t, t)]) 

To už je "elementární" integrál, pro jeho vyhodnocení použijeme příkaz value. 

> v:=value(g);
 

(Typesetting:-mprintslash)([v := 1/2*ln(t)], [1/2*ln(t)]) 

Maple používá ln(t)namísto Protože nezpůsobí nám to v tomto případě problémy. 

Zpětnou substitucí se vrátíme zpět k původní proměnné. 

> subs(t=x^2+1, v);
 

1/2*ln(x^2+1) 

Příklad 1 

> i1:=Int((1+ln(x))^4/x, x);
 

(Typesetting:-mprintslash)([i1 := Int((1+ln(x))^4/x, x)], [Int((1+ln(x))^4/x, x)]) 

> i1=changevar((1+ln(x))=t, i1, t);
 

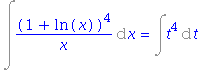
Int((1+ln(x))^4/x, x) = Int(t^4, t) 

> value(rhs(%));
 

1/5*t^5 

> subs(t=ln(x)+1, %);
 

1/5*(1+ln(x))^5 

> testeq(diff(%,x)=integrand(i1));
 

true 

Příklad 2 

> assume(x>-1);
 

> additionally(x>1);
 

> i2:=Int(sqrt(1-x^2), x);
 

(Typesetting:-mprintslash)([i2 := Int((1-x^2)^(1/2), x)], [Int((1-x^2)^(1/2), x)]) 

> i2=changevar(x=sin(t), i2, t);
 

Int((1-x^2)^(1/2), x) = Int((1-sin(t)^2)^(1/2)*cos(t), t) 

> value(rhs(%));
 

1/2*(1-sin(t)^2)^(1/2)*sin(t)+1/2*t 

 

> i2=subs(t=arcsin(x), %);
 

Int((1-x^2)^(1/2), x) = 1/2*(1-sin(arcsin(x))^2)^(1/2)*sin(arcsin(x))+1/2*arcsin(x)
Int((1-x^2)^(1/2), x) = 1/2*(1-sin(arcsin(x))^2)^(1/2)*sin(arcsin(x))+1/2*arcsin(x) 

> combine(%);
 

Int((1-x^2)^(1/2), x) = 1/2*(1-x^2)^(1/2)*x+1/2*arcsin(x) 

> value(i2);
 

1/2*(1-x^2)^(1/2)*x+1/2*arcsin(x) 

> rationalize(simplify(diff(%,x)));
 

(1-x^2)^(1/2) 

Příklad 3 

> restart; with(student):
 

> i3:=Int(cos(x)^5 *sin(x)^2, x);
 

(Typesetting:-mprintslash)([i3 := Int(cos(x)^5*sin(x)^2, x)], [Int(cos(x)^5*sin(x)^2, x)]) 

> i3=changevar(sin(x)=t, i3, t);
 

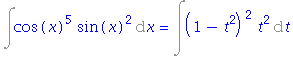
Int(cos(x)^5*sin(x)^2, x) = Int((1-t^2)^2*t^2, t) 

> value(rhs(%));
 

1/7*t^7-2/5*t^5+1/3*t^3 

> i3=subs(t=sin(x), %);
 

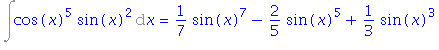
Int(cos(x)^5*sin(x)^2, x) = 1/7*sin(x)^7-2/5*sin(x)^5+1/3*sin(x)^3 

Příklad 4 

> i4:=Int(1/sin(x), x);
 

(Typesetting:-mprintslash)([i4 := Int(1/sin(x), x)], [Int(1/sin(x), x)]) 

> i4=changevar(cos(x)=t, i4, t);
 

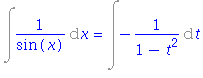
Int(1/sin(x), x) = Int(-1/(1-t^2), t) 

> simplify(%);
 

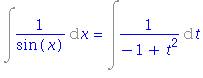
Int(1/sin(x), x) = Int(1/(-1+t^2), t) 

> rhs(%);
 

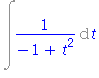
Int(1/(-1+t^2), t) 

Integrál řešíme rozkladem na parciálni zlomky. 

> integrand(%);
 

1/(-1+t^2) 

> convert(%, 'parfrac', t);
 

1/2/(t-1)-1/2/(t+1) 

> int(%, t);
 

1/2*ln(t-1)-1/2*ln(t+1) 

> subs(t=cos(x), %);
 

1/2*ln(cos(x)-1)-1/2*ln(cos(x)+1) 

> v:=%;
 

(Typesetting:-mprintslash)([v := 1/2*ln(cos(x)-1)-1/2*ln(cos(x)+1)], [1/2*ln(cos(x)-1)-1/2*ln(cos(x)+1)]) 

> diff(v,x);
 

-1/2*sin(x)/(cos(x)-1)+1/2*sin(x)/(cos(x)+1) 

> testeq(%=integrand(i4));
 

true 

Příklad 5 

> i5:=Int(1/(1+sin(x)^2), x);
 

(Typesetting:-mprintslash)([i5 := Int(1/(1+sin(x)^2), x)], [Int(1/(1+sin(x)^2), x)]) 

> i5=changevar(tan(x)=t, i5, t);
 

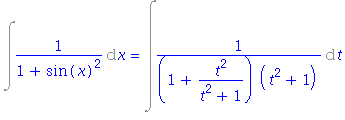
Int(1/(1+sin(x)^2), x) = Int(1/((1+t^2/(t^2+1))*(t^2+1)), t) 

> simplify(rhs(%));
 

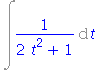
Int(1/(2*t^2+1), t) 

> value(%);
 

1/2*2^(1/2)*arctan(t*2^(1/2)) 

> i5=subs(t=tan(x), %);
 

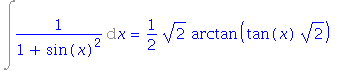
Int(1/(1+sin(x)^2), x) = 1/2*2^(1/2)*arctan(tan(x)*2^(1/2)) 

> v:=diff(rhs(%), x);
 

(Typesetting:-mprintslash)([v := (1+tan(x)^2)/(1+2*tan(x)^2)], [(1+tan(x)^2)/(1+2*tan(x)^2)]) 

> testeq(v=integrand(i5));
 

true 

Příklad 6 

> assume(x>1);
 

> i6:=Int(1/x*sqrt((x+1)/(x-1)), x);
 

(Typesetting:-mprintslash)([i6 := Int(((x+1)/(x-1))^(1/2)/x, x)], [Int(((x+1)/(x-1))^(1/2)/x, x)]) 

 

> simplify(changevar((x+1)/(x-1)=t^2, i6, t));
 

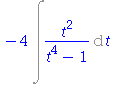
-4*Int(t^2/(t^4-1), t) 

> (-4)*convert(integrand(%), parfrac, t);
 

-2/(t^2+1)-1/(t-1)+1/(t+1) 

> int(%, t);
 

-2*arctan(t)-ln(t-1)+ln(t+1) 

> subs(t=sqrt((x+1)/(x-1)), %);
 

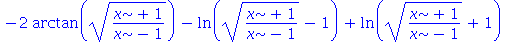
-2*arctan(((x+1)/(x-1))^(1/2))-ln(((x+1)/(x-1))^(1/2)-1)+ln(((x+1)/(x-1))^(1/2)+1) 

> v:=(diff(%,x));
 

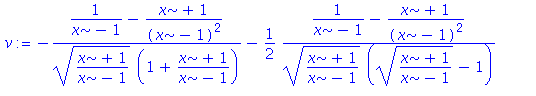
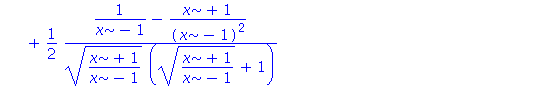
(Typesetting:-mprintslash)([v := -(1/(x-1)-(x+1)/(x-1)^2)/(((x+1)/(x-1))^(1/2)*(1+(x+1)/(x-1)))-1/2*(1/(x-1)-(x+1)/(x-1)^2)/(((x+1)/(x-1))^(1/2)*(((x+1)/(x-1))^(1/2)-1))+1/2*(1/(x-1)-(x+1)/(x-1)^2)/((...
(Typesetting:-mprintslash)([v := -(1/(x-1)-(x+1)/(x-1)^2)/(((x+1)/(x-1))^(1/2)*(1+(x+1)/(x-1)))-1/2*(1/(x-1)-(x+1)/(x-1)^2)/(((x+1)/(x-1))^(1/2)*(((x+1)/(x-1))^(1/2)-1))+1/2*(1/(x-1)-(x+1)/(x-1)^2)/((... 

> rationalize(v);
 

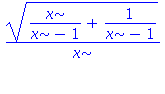
(x/(x-1)+1/(x-1))^(1/2)/x 

> normal(%);
 

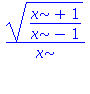
((x+1)/(x-1))^(1/2)/x 

> testeq(%=integrand(i6));
 

true 

>