Integrace racionalní lomené funkce
Maple umožňuje rozložit racionalní lomenou funkci na parcialní zlomky příkazem convert(f, parfrac, promenna).
| > | convert((12*x+7)/(x^2-9*x+18), parfrac, x); |
![]()
Příklad 1
| > | i1:=Int(x/(x^3-1), x); |
![(Typesetting:-mprintslash)([i1 := Int(x/(x^3-1), x)], [Int(x/(x^3-1), x)])](imagesparfrac/parfrac_2.gif)
| > | with(student): |
| > | convert(integrand(i1), parfrac, x); |
![]()
| > | int(%,x); |
![]()
Příklad 2
| > | i2:=Int((x^7+7*x-1)/(x^9+2*x^6+x^3), x); |
![(Typesetting:-mprintslash)([i2 := Int((x^7+7*x-1)/(x^9+2*x^6+x^3), x)], [Int((x^7+7*x-1)/(x^9+2*x^6+x^3), x)])](imagesparfrac/parfrac_5.gif)
| > | convert(integrand(i2), parfrac, x); |
![]()
| > | int(%,x); |
![]()
![]()
| > | normal(diff(%,x), expanded); |
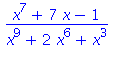
Trigonometrické substituce
Příklad 3
| > | i3:=Int(x^3*sqrt(4-x^2), x); |
![(Typesetting:-mprintslash)([i3 := Int(x^3*(4-x^2)^(1/2), x)], [Int(x^3*(4-x^2)^(1/2), x)])](imagesparfrac/parfrac_10.gif)
| > | changevar(x=2*sin(t), i3, t); |
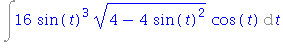
| > | value(%); |
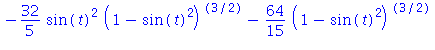
| > | subs(sin(t)=x/2, %); |
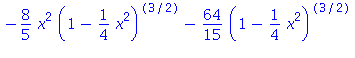
| > | i3=simplify(%); |
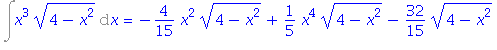
| > | diff(rhs(%),x); |
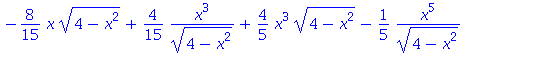
![]()
| > | rationalize(%); |
![]()
Příklad 4
| > | i4:=Int(1/(9+x^2), x); |
![(Typesetting:-mprintslash)([i4 := Int(1/(9+x^2), x)], [Int(1/(9+x^2), x)])](imagesparfrac/parfrac_18.gif)
| > | changevar(x=tan(t), i4, t); |
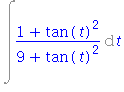
| > | value(%); |
![]()
| > | i4=subs(tan(t)=x, %); |
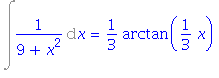
| > | normal(diff(rhs(%), x)); |
![]()
Příklad 5
Nakreslete graf primitivní funkce k funkci ![]() na intervalu
na intervalu ![]() .
.
| > | f:=x->1/(2-cos(x)); |
![]()
| > | i:=int(f(x), x); |
![]()
| > | plot(i, x=0..2*Pi, discont=true, color=black); |
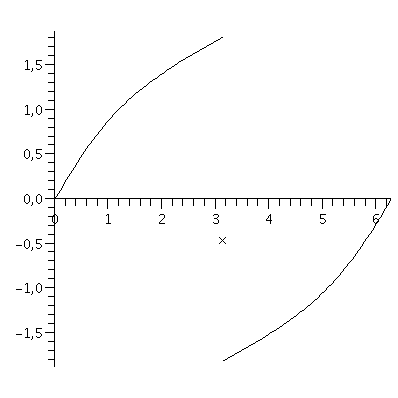
Ze získaného grafu je zřejmé, ze se nejedná o funkci primitivní na intevalu ![]() , protože není na tomto
, protože není na tomto
intervalu spojitá. Primitivní funkci zkonstruujeme nasledujicím způsobem
| > | limit(i, x=Pi, left); |
![]()
| > | limit(i, x=Pi, right); |
![]()
| > | i1:=i+2/3*Pi*sqrt(3); |
![]()
| > | p1:=plot(i, x=0..Pi): |
| > | p2:=plot(i1, x=Pi..2*Pi): |
| > | with(plots): |
| > | display({p1,p2}, color=black); |
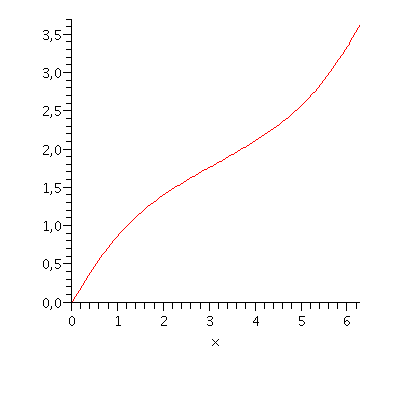
| > |