![(Typesetting:-mprintslash)([i1 := Int(x^2, x = 1 .. 2)], [Int(x^2, x = 1 .. 2)])](imagesurc/newtonleibniz_1.gif)
Newtonova - Leibnizova formule
S využitím Newtonovy-Leibnizovy formule vypočtěte určité integrály:
| > | i1:=Int(x^2, x=1..2); |
![(Typesetting:-mprintslash)([i1 := Int(x^2, x = 1 .. 2)], [Int(x^2, x = 1 .. 2)])](imagesurc/newtonleibniz_1.gif)
| > | F:=unapply(int(x^2,x),x); |
![]()
| > | F(2)-F(1); |
![]()
Přímým výpočtem pomocí Maplu dostaváme
| > | i1=value(i1); |
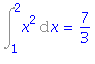
| > | i2:=Int(1/x^2, x=-1..1); |
![(Typesetting:-mprintslash)([i2 := Int(1/x^2, x = -1 .. 1)], [Int(1/x^2, x = -1 .. 1)])](imagesurc/newtonleibniz_5.gif)
Pokud bychom "slepě" použili předcházející postup, dostaneme
| > | F:=unapply(int(1/x^2,x),x); |
![]()
| > | F(1)-F(-1); |
![]()
což zjevně neplatí, protože
| > | plot(1/x^2, x=-1..1, y=0..10, discont=true); |
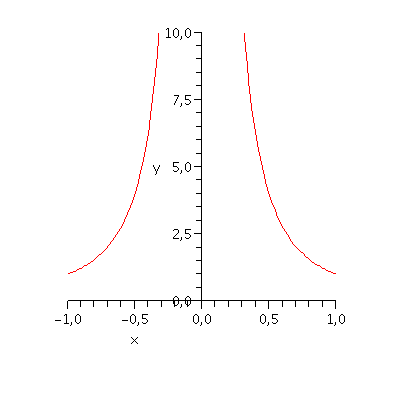
f není na intervalu 〈-1,1〉 ohraničená, a proto určitý integrál diverguje
| > | Int(1/x^2, x=-1..1):%=value(%); |
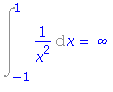
| > | i3:=Int(1/(2-cos(x)), x=0..2*Pi); |
![(Typesetting:-mprintslash)([i3 := Int(1/(2-cos(x)), x = 0 .. 2*Pi)], [Int(1/(2-cos(x)), x = 0 .. 2*Pi)])](imagesurc/newtonleibniz_10.gif)
| > | F:=unapply(int(1/(2-cos(x)),x),x); |
![]()
Opět "slepou" aplikací Newtonovy-Leibnizovy formule dostáváme
| > | F(2*Pi)-F(0); |
![]()
což je očividně chybný výsledek, protože integrand je kladná funkce, takže integrál musí mít kladnou hodnotu.
| > | plot(1/(2-cos(x)), x=0..2*Pi); |
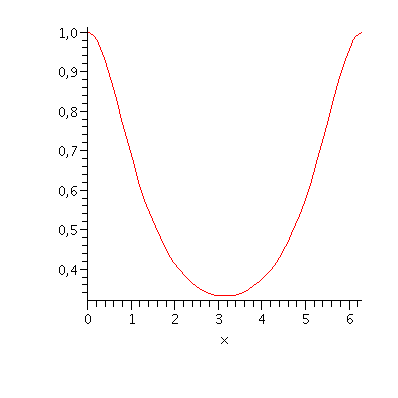
| > | Int(1/(2-cos(x)), x=0..2*Pi):%=value(%); |
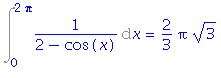
(pro spravný výpočet bychom museli použít konstrukci primitivní funkce z minulého cvičení).