Metody statistického odhadu
veličina odvozená ze vzorku dat (statistický soubor) = statistika (odhad)
viz úvod (různé odhady minimalizují různé veličiny)
efektivnost
- minimalizuje $D(\hat{\theta})$ - nejmenší mezi všemi = efektivní odhad
- asymptotická efektivnost - pro $N \to \infty$
konzistence
- pro $N \to \infty$ konverguje $\hat{\theta_0} \to \theta_0$ a $V(\theta) \to 0$
- např. aritmetický průměr není konzist. odhadem param. polohy $\theta_0$ Cauchyho rozdělení $$\frac{1}{1+(x+\theta_0)^2}$$
nestrannost (unbiasedness)
- $E(\hat{\theta_0}) = \theta_0$
- např. odhad disperze aritm. průměru dat (s norm. rozdělením) pomocí max. věrohodnosti není nestranný
robustnost
- odolnost vůči odlehlým pozorováním (vybočující hodnoty)
Příklad: jsou-li $x_i$ rovnom. rozdělené náhod. proměnné z interv. $(0, \theta)$, pak $max(x_1,x_2..x_n)$ je konzistentním, ale vychýleným odhadem $\theta$
Nejčastěji odhad intervalový (interval spolehlivosti, "konfidenční") $\hat{\theta_0} \pm \sigma$
$$P(\hat{\theta_a} < \theta_0 < \hat{\theta_b}) = \alpha$$
(zadaná hodnota koeficientu spolehlivosti $\alpha$)
Příklad
$y_1,...,y_N$ nezávislé, rozd. $N(\theta_0,\sigma)$ se známým $\sigma$
odhad $$\hat{\theta_0}=\frac{1}{N} \sum_i^N {y_i}$$ má rozdělení $N(\theta_0,\sigma/\sqrt{N})$
$\hat{\theta_0} \pm \sigma/\sqrt{N}$ ... 68% interval (prst, že obsahuje $\theta_0$)
$\hat{\theta_0} \pm 2\sigma/\sqrt{N}$ ... 95% interval
efektivita odhadu středu rozdělení
sada hodnot s D(x)=1
| rozdělení | median | aritm. průměr | (max+min)/2 |
|---|---|---|---|
| normální | $\pi/(2N)$ | $1/N$ | $\pi^2/(12 \ln N)$ |
| rovnoměrné | $1/(4N)$ | $1/(12N)$ | $1/(2N^2+6N+4)$ |
| dvoj-exponenciální | $1/(2N)$ | $2/N$ | $\pi^2/12$ |
| Cauchyho | $\pi^2/(4N)$ | $\infty$ | $\infty$ |
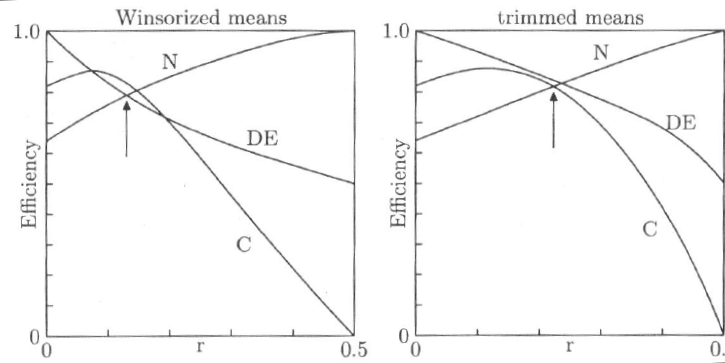
Efektivita po ořezání v závislosti na param. $r=(N-n)/2N$ (n extrémních hodnot odstraněno/nahrazeno) po ořezu (vpravo) a winsorizaci (vlevo)