kruh, vyšší hustota ve středu [Point(3)]
cl__1 = 0.1;
Point(1) = {-0.5, 0, 0, cl__1};
Point(2) = {0, 0.5, 0, cl__1};
Point(3) = {0, 0, 0, 0.02};
Point(4) = {0, -0.5, 0, cl__1};
Point(5) = {0.5, 0, 0, cl__1};
Circle(1) = {1, 3, 2};
Circle(2) = {2, 3, 5};
Circle(3) = {5, 3, 4};
Circle(4) = {4, 3, 1};
Line(5) = {1, 3};
Line(6) = {3, 5};
Line Loop(8) = {1, 2, -6, -5};
Plane Surface(8) = {8};
Line Loop(10) = {4, 5, 6, 3};
Plane Surface(10) = {10};generování skriptově pomocí gmsh
import subprocess as sp
#wdir="C:/Users/Admin/Dropbox/Notebook/Temp/"
wdir="/home/jupyter/note/FEM/"
#gmsh_run='C:/Program Files/Gmsh/gmsh.exe'
gmsh_run="/usr/bin/gmsh"
pars=[gmsh_run,'work/ex2.geo','-3','-o','work/ex2new1.msh']
#pars+=['-clmin',str(0.005)]
sp.run(pars,cwd=wdir)
soubor .msh vytvořen v textovém formátu = lze načíst ručně
import numpy as np
import sys
#sys.path.append("/home/limu/Code/Monty")
import fem_laplace as fl
%matplotlib inline
from matplotlib import pyplot as pl
nodes,faces=fl.load("work/ex2new1.msh","./",seltype=1)
#nodes,faces=fl.load("ex2.msh","./",seltype=1)
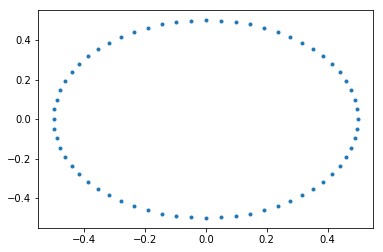
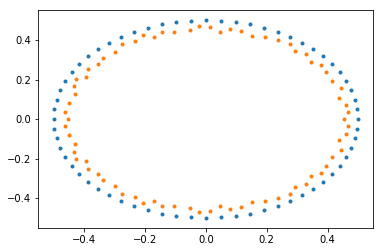
pl.plot(nodes[:,1],nodes[:,0],'.')
dist=np.sqrt(nodes[:,0]**2+nodes[:,1]**2)
amax=dist.max()
ef=dist>amax-0.01
#ef=faces[2][edgsel]
pl.plot(nodes[ef,1],nodes[ef,0],'r.')
len(faces[1])
30
raději ale použijeme udržovanou knihovnu
import meshio
remesh=meshio.read("work/ex2new2.msh")
pts=remesh.points
list(remesh.cells_dict.keys())
['vertex', 'line', 'triangle']
cor=remesh.cells_dict['triangle'][6]
tri=pts[cor]
tri
array([[0.41118103, 0. , 0. ],
[0.43202587, 0.04851823, 0. ],
[0.45388959, 0. , 0. ]])
def pplot(cor,mshi=0.2):
tri=pts[cor]
cen=tri.mean(0)
tri=tri*(1-mshi)+cen*mshi
for i in range(3):
pl.plot([tri[i][0],tri[(i+1)%3][0]], [tri[i][1],tri[(i+1)%3][1]],'r')
#jenom nekktere elementy
for c in remesh.cells_dict['triangle'][::10]:
pplot(c)
np.min(remesh.cells_dict['triangle'])
0
surf=[]
for cor in remesh.cells_dict['triangle']:
fac=pts[cor].copy()
fac[:,2]=1
surf.append(abs(np.linalg.det(fac)/2))
pl.hist(surf,20);
#rychlejsi metoda (narocnejsi na pamet)
allcor=pts[remesh.cells_dict['triangle']]
allcor[:,:,2]=1
surf2=np.abs(np.linalg.det(allcor))/2
max(abs(surf2-surf))
0.0
ind=[[0,1],[1,2],[2,0]]
leng=[]
for cor in remesh.cells_dict['triangle']:
fac=pts[cor].copy()
fac[:,2]=1
leng.append(np.sqrt([((fac[d][1]-fac[d][0])**2).sum() for d in ind]))
leng=np.array(leng)
leng.shape
(1952, 3)
#jak spocitat delky hran "vektorove"
d=ind[1]
((np.r_[1,-1].reshape(2,1)*cont[0][d]).sum(0)**2).sum()
0.0023785658116376464
zz=np.r_[1,-1].reshape(2,1)
leng2=np.sqrt([((allcor[:,d]*zz).sum(1)**2).sum(1) for d in ind]).T
pl.hist(leng.flat,20);
np.where(leng>0.1)
(array([], dtype=int64), array([], dtype=int64))
#pomer nejdelsi a nejkratsi strany trojuhelnika (hledame prilis "spicate" elementy)
rat=leng.min(axis=1)/leng.max(axis=1)
pl.hist(rat);
#umime secist plochu?
sum(surf),np.pi*0.5**2
(0.784137122636484, 0.7853981633974483)
#body na okraji (totez co v uvodu)
dist=np.sqrt(pts[:,0]**2+pts[:,1]**2)
amax=dist.max()
edgsel=dist>amax-0.01
edgcor=pts[edgsel]
pl.plot(edgcor[:,0],edgcor[:,1],'.')
sum(edgsel)
64
#sousedni body
nint=len(pts)-sum(edgsel) #pocet internich bodu
edgind=np.r_[:len(edgsel)][edgsel]
nearcor=[cor for cor in remesh.cells_dict['triangle'] if np.any([a in edgind for a in cor])]
nearind=set(np.array(nearcor).ravel())-set(edgind)
#nearind=[i for i in boundind if not i in edgind]
nearind=list(nearind)
len(nearind)
74
edgcor=pts[edgsel]
pl.plot(edgcor[:,0],edgcor[:,1],'.')
nearcor=pts[nearind]
pl.plot(nearcor[:,0],nearcor[:,1],'.')
[<matplotlib.lines.Line2D at 0x24da397e0f0>]
