3-D

nyní kromě triangles máme ještě tetra - čtyřstěny

import meshio
ms1=meshio.read("work/ex3new2.msh")

%matplotlib inline
from matplotlib import pyplot as pl
sel=ms1.points[:,2]==0
pos=ms1.points[sel,:2].T
pl.plot(pos[0],pos[1],'+')
pl.title("base plane")

Text(0.5,1,'base plane')

ms1.cells[0][1].max(),ms1.cells[1][1].max()

(70, 71)

Physical Surfaces/Volumes

Pokud v .geo souboru definujeme fyzické oblasti, budou na výstupu v meshi jen elementy (cells), které jsou obsaženy v těchto oblastech. Indexy přiřazené k oblastem jsou v meshio propojeny s těmito elementy pomocí položky gmsh:physical.

labels=ms1.cell_data_dict['gmsh:physical']['triangle']
import numpy as np
np.unique(labels)

array([ 9, 10], dtype=int32)

tree=ms1.points[ms1.cells[0][1]] # totez co ms1.cells_dict['triangle']
tree[labels==9,:,2]

array([[0.125     , 0.        , 0.        ],
       [0.125     , 0.        , 0.        ],
       [0.5       , 0.375     , 0.375     ],
       [0.        , 0.        , 0.12305779],
       [0.125     , 0.        , 0.12305779],
       [0.        , 0.10069506, 0.        ],
       [0.10069506, 0.12305779, 0.        ],
       [0.125     , 0.14116813, 0.        ],
       [0.10069506, 0.        , 0.14116813],
       [0.375     , 0.23014556, 0.25      ],
       [0.375     , 0.375     , 0.23014556],
       [0.125     , 0.25      , 0.14116813],
       [0.23014556, 0.14116813, 0.25      ],
       [0.375     , 0.25      , 0.23014556],
       [0.125     , 0.12305779, 0.25      ],
       [0.23014556, 0.25      , 0.12305779],
       [0.23014556, 0.10069506, 0.14116813],
       [0.23014556, 0.12305779, 0.10069506]])

#ctvrtiny plaste 
for t in tree[labels==9]:
    tt=np.r_[t,[t[0]]]
    pl.plot(tt[:,0],tt[:,2],'g')
for t in tree[labels==10]:
    tt=np.r_[t,[t[0]]]
    pl.plot(tt[:,0],tt[:,2],'b')
    

from mpl_toolkits.mplot3d import Axes3D
fig=pl.figure(figsize=(10,10))
ax = fig.add_subplot(111,projection='3d')
ax.view_init(30, 80)
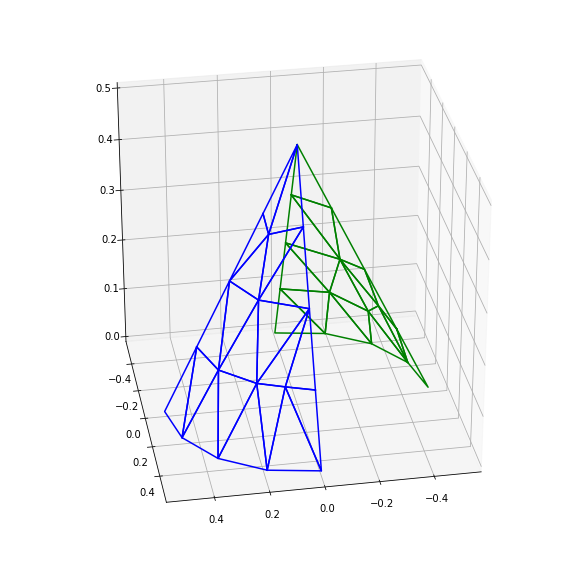
for t in tree[labels==9]:
    tt=np.r_[t,[t[0]]]
    ax.plot(tt[:,0],tt[:,1],tt[:,2],'g')
for t in tree[labels==10]:
    tt=np.r_[t,[t[0]]]
    ax.plot(tt[:,0],tt[:,1],tt[:,2],'b')

from mpl_toolkits.mplot3d import Axes3D
fig.add_subplot(111,projection='3d')

<matplotlib.axes._subplots.Axes3DSubplot at 0x7f0b08eff128>

import numpy as np
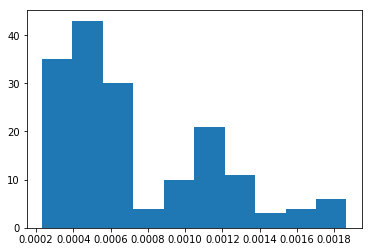
vols=[]
for cor in ms1.cells_dict['tetra']:
    tetra=ms1.points[cor]
    vols.append(np.abs(np.linalg.det(tetra[1:]-tetra[0])/6))
pl.hist(vols);
sum(vols)

0.1217369265741864

#opet to lze provest efektivneji
tree2=ms1.points[ms1.cells_dict['tetra']] # totez co ms1.cells_dict['triangle']
tree2[:,1:]-=tree2[:,0][:,np.newaxis,:]
vols2=np.linalg.det(tree2[:,1:])/6
np.all(vols2==vols)

True

úkol: zkuste dopočítat následující momentové integrály (stačí bez osy z, záměna os je triviální)

$M_T(1,0,0)=1/4\ (x_a+x_b+x_c+x_d)$
$M_T(0,1,0)=1/4\ (y_a+y_b+y_c+y_d)$

$M_T(2,0,0)=1/10\ (x^2_a+x^2_b+x^2_c+x^2_d+x_a x_b+x_b x_c+x_c x_d+x_a x_c+x_a x_d+x_b x_d)$

$M_J(1,1,0)=1/20\ \left(2(x_a y_a+x_b y_b+x_c y_c+x_d y_d) +x_a y_b+x_a y_c+x_a y_d+x_b y_a+x_b y_c+x_b y_d +x_c y_a+x_c y_b+x_c y_d+x_d y_a+x_d y_b+x_d y_c\right)$