In [1]:
%matplotlib inline
from matplotlib.pyplot import *
from math import sqrt,pi
from numpy import random,histogram,r_,array,exp,polyfit
nexp=10000
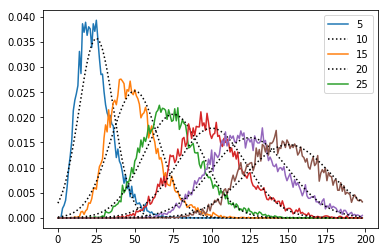
sim=array([random.uniform(0,10,30).reshape(5,6).sum(0).cumsum() for i in range(nexp)]).transpose()
bin=r_[0:200:1.]
import matplotlib.pyplot as rp
his1=[histogram(sim[0],bin)[0]/float(nexp)]
a=rp.plot(bin[:-1],his1[0])[0].axes
i=0
sig=sqrt((i+1)*500./12.)
a.plot(bin[:-1],1/sqrt(2*pi)/sig*exp(-(bin[:-1]-(i+1)*25)**2/2/sig**2),'k:')
for i in range(1,len(sim)):
s=sim[i]
his1.append(histogram(s,bin)[0]/float(nexp))
sig=sqrt((i+1)*500./12.)
a.plot(bin[:-1],his1[-1])
a.plot(bin[:-1],1/sqrt(2*pi)/sig*exp(-(bin[:-1]-(i+1)*25)**2/2/sig**2),'k:')
sum(his1[-3])
a.legend(r_[5:31:5])
a
Out[1]: