

 je
diferencovatelná v bodě x0,
jestliže existuje reálné číslo A takové, že
je
diferencovatelná v bodě x0,
jestliže existuje reálné číslo A takové, že[Další] [Předchozí] [Předchozí – na konec] [Na konec] [Výše]
Diferenciálem funkce f jedné proměnné v bodě x0
rozumíme přírůstek funkce na tečně vedené ke grafu funkce v bodě
[x0,f(x0)].
V tomto případě existence diferenciálu neboli
diferencovatelnost funkce je ekvivalentní existenci derivace
v bodě x0. Připomeňme, že f :


 je
diferencovatelná v bodě x0,
jestliže existuje reálné číslo A takové, že
je
diferencovatelná v bodě x0,
jestliže existuje reálné číslo A takové, že

U funkce n proměnných (n ≥
2) je totální diferenciál definován analogicky: je to
přírůstek funkce na tečné nadrovině vedené ke grafu funkce bodem
x0 
 n.
Přesnou definici pojmu tečná nadrovina uvedeme později;
v podstatě je to
nadrovina (tj. afinní podprostor dimenze n −
1), která má s grafem
funkce lokálně (tj. v okolí bodu, kde tečnou nadrovinu
sestrojujeme) společný právě jeden bod.
n.
Přesnou definici pojmu tečná nadrovina uvedeme později;
v podstatě je to
nadrovina (tj. afinní podprostor dimenze n −
1), která má s grafem
funkce lokálně (tj. v okolí bodu, kde tečnou nadrovinu
sestrojujeme) společný právě jeden bod.
Se zavedením těchto pojmů okamžitě vznikají tyto otázky: Kdy v daném bodě existuje tečná nadrovina ke grafu funkce neboli kdy je funkce diferencovatelná? Stačí k tomu pouhá existence parciálních derivací jako u funkce jedné proměnné?
Odpovědi na tyto a další podobné otázky jsou obsahem této kapitoly.
Nejdříve definujme pojem diferencovatelnosti a diferenciálu pro funkce dvou proměnných.
Poznámka 4.1. i) Ekvivalentní zápis definice diferencovatelnosti
funkce dvou proměnných je tento: existují A,B 
 a funkce
a funkce  :
:
 2
2 
 tak, že platí
tak, že platí
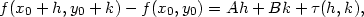 |
(4.2) |
kde
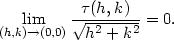 |
(4.3) |
ii) Jmenovatel limity ve výrazu (4.1) je velikost vektoru
(h,k)
v euklidovské metrice. V odstavci 2.1 jsme zdůraznili
ekvivalentnost metrik  1,
1, 2 a
2 a

 . Proto
nahradíme-li výraz
. Proto
nahradíme-li výraz 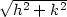 výrazem
výrazem  h
h +
+  k
k (velikost
(h,k)
v metrice
(velikost
(h,k)
v metrice  1)
nebo výrazem max{
1)
nebo výrazem max{ h
h ,
, k
k } (velikost
(h,k)
v metrice
} (velikost
(h,k)
v metrice 
 ), dostaneme
definici ekvivalentní s Definicí 4.1
.
), dostaneme
definici ekvivalentní s Definicí 4.1
.
V předchozí kapitole jsme ukázali, že pro funkce dvou a více proměnných z existence parciálních ani směrových derivací neplyne spojitost. Následující dvě věty ukazují, že diferencovatelnost funkce je tou „správnou“ vlastností, která implikuje spojitost a některé další vlastnosti funkce.
Důkaz. Z diferencovatelnosti funkce f v bodě [x0,y0] plyne
![(h,kli)→m(0,0)[f(x0+ h,y0 + k)− f(x0,y0)] = (h,kl)im→(0,0)[Ah + Bk + τ(h, k)] = 0,](diferencialni-pocet330x.png)
 (0,0)
(0,0) (h,k) =
0. Odtud
(h,k) =
0. Odtud
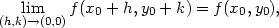
Poznámka 4.2. Opak této věty neplatí. Je-li
funkce spojitá, nemusí být diferencovatelná, např. f(x,y) =
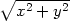 v bodě [0,0].
v bodě [0,0].
Věta 4.2. Je-li funkce f diferencovatelná v bodě [x0,y0], pak má v tomto bodě parciální derivace a platí A = fx(x0,y0), B = fy(x0,y0), tj.
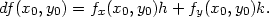 |
(4.4) |
Důkaz. Položme
v (4.1)
k =
0. Pak limh 0
0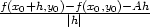 = 0, a proto
= 0, a proto
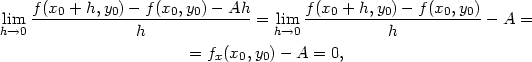
|
Poznámka 4.3. i) Přírůstky h,k nezávisle proměnných x,y v definici diferenciálu se často značí dx, dy (především ve starší literatuře a v literatuře s fyzikálním zaměřením).
ii) Je-li funkce f diferencovatelná v každém bodě množiny M, má v každém bodě této množiny diferenciál, který je funkcí čtyř proměnných: x,y,h,k. Označíme-li dx = x − x0 = h, dy = y − y0 = k, dostáváme, že diferenciál funkce f je

iii) Diferenciál se používá k přibližnému
výpočtu funkčních hodnot. Zanedbáme-li funkci  , z rovnice (4.2
) plyne
, z rovnice (4.2
) plyne
 |
(4.5) |
Geometrický
význam
totálního diferenciálu. Rovina v  3
o rovnici z = Ax
+ By +
C se nazývá tečnou rovinou ke grafu funkce z =
f(x,y)
v bodě T = [x0,y0,f(x0,y0)],
platí-li
3
o rovnici z = Ax
+ By +
C se nazývá tečnou rovinou ke grafu funkce z =
f(x,y)
v bodě T = [x0,y0,f(x0,y0)],
platí-li

Má-li tato rovina procházet bodem T, musí tento bod vyhovovat rovnici roviny, tj. f(x0,y0) = Ax0 + By0 + C, odkud z = A(x−x0) + B(y −y0) + f(x0,y0). Tato rovina je tečnou rovinou, jestliže existuje diferenciál funkce v bodě [x0,y0], tj. podle Věty 4.2 je A = fx(x0,y0),B = fy(x0,y0). Rovnice tečné roviny má tvar
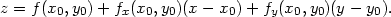 |
(4.6) |
Odtud je vidět, že diferenciál funkce v daném
bodě je přírůstek funkce na tečné rovině. Funkce  (h,k)
z Poznámky 4.1
určuje rozdíl mezi skutečným
přírůstkem a přírůstkem na tečné rovině. Rovnice tečné roviny je
nejlepší lineární aproximací funkce f(x,y)
v okolí bodu [x0,y0].
(h,k)
z Poznámky 4.1
určuje rozdíl mezi skutečným
přírůstkem a přírůstkem na tečné rovině. Rovnice tečné roviny je
nejlepší lineární aproximací funkce f(x,y)
v okolí bodu [x0,y0].
Příklad 4.2. i) Pomocí totálního diferenciálu přibližně vypočtěte:
| a) 1,042,02; | b)  . . |
Řešení. a) K výpočtu použijeme diferenciál funkce f(x,y) = xy v bodě [1,2] s diferencemi dx = 0,04, dy = 0,02. Platí


b) K výpočtu použijeme diferenciál funkce
f(x,y) =
 v bodě [3,4]
s diferencemi dx
= −0,02, dy =
0,05. Platí
v bodě [3,4]
s diferencemi dx
= −0,02, dy =
0,05. Platí

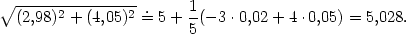
ii) Napište rovnici tečné roviny grafu funkce z = x2 + y2 v bodě [1,1,?].
Řešení. Dosazením do funkčního předpisu najdeme z-ovou souřadnici dotykového bodu z = 12 + 12 = 2. Nyní přímým dosazením do vzorce pro tečnou rovinu dostáváme její rovnici z = 2 + 2(x − 1) + 2(y − 1), tj. 2x + 2y − z − 2 = 0.
Jak již víme, ze samotné existence parciálních derivací funkce v bodě [x0,y0] neplyne diferencovatelnost (viz příklad 3.2 ). Jsou-li však tyto derivace v tomto bodě spojité, je diferencovatelnost zaručena, jak ukazuje následující věta.
Věta 4.3. Má-li funkce f v bodě [x0,y0] spojité parciální derivace 1. řádu, pak má v tomto bodě také diferenciál.
Důkaz. Ze spojitosti parciálních derivací fx,fy v bodě [x0,y0] plyne jejich existence v jistém okolí tohoto bodu. Podle Věty 3.5 platí
![f(x0 + h,y0 + k) − f(x0,y0)− fx(x0,y0)h− fy(x0,y0)k lim ---------------------√--2---2----------------------= (h,k)→(0,0) h + k = lim fx(x0-+ϑ1h,-y0+k)h+fy(x0,√y0+-ϑ2k)k−-fx(x0,y0)h−-fy(x0,y0)k-= (h,k)→(0,0) h2 + k2 h = lim [fx(x0 + ϑ1h,y0 + k)− fx(x0,y0)]⋅√--2----2+ (h,k)→(0,0) h + k + lim [f (x ,y + ϑ k) − f (x ,y )]⋅ √--k-----= 0, (h,k)→(0,0) y 0 0 2 y 0 0 h2 + k2](diferencialni-pocet347x.png)
|
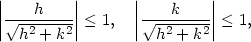
Příklady funkcí, které jsou, resp. nejsou diferencovatelné v daném bodě, viz příklady 13.4 , 13.5 , 13.9 .
Obecně –
funkce n proměnných f :  n
n

 je
diferencovatelná v bodě
x∗
je
diferencovatelná v bodě
x∗
 n,
jestliže existuje a
= (a1,…,an)
n,
jestliže existuje a
= (a1,…,an) 
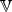 n takové, že pro
h =
(h1,…,hn)
n takové, že pro
h =
(h1,…,hn) 
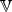 n platí
n platí


 h
h
 =
=  a
a 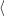 a,h
a,h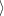 = ∑ i=1naihi
je obvyklý skalární součin v
= ∑ i=1naihi
je obvyklý skalární součin v  n.
Diferenciálem funkce
f v bodě
x∗ pak
rozumíme lineární funkci
definovanou předpisem
n.
Diferenciálem funkce
f v bodě
x∗ pak
rozumíme lineární funkci
definovanou předpisem

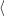 a,h
a,h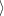 .
Stejně jako ve Větách 4.1 a 4.2, z existence
diferenciálu v bodě
x∗ plyne spojitost
funkce a existence parciálních
derivací v tomto
bodě a pro vektor těchto
parciálních derivací
f
.
Stejně jako ve Větách 4.1 a 4.2, z existence
diferenciálu v bodě
x∗ plyne spojitost
funkce a existence parciálních
derivací v tomto
bodě a pro vektor těchto
parciálních derivací
f (x∗) platí
f
(x∗) platí
f (x∗) = a, tj.
(x∗) = a, tj. 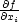 (x∗) = ai, i =
1,…,n.
(x∗) = ai, i =
1,…,n.
Na závěr tohoto odstavce ukážeme, že z diferencovatelnosti funkce plyne – kromě spojitosti a existence parciálních derivací – také existence směrové derivace ve směru libovolného vektoru. Ukážeme rovněž, jak lze pomocí diferenciálu tyto směrové derivace spočítat.
Věta 4.4. Předpokládejme, že funkce
f :
 n
n

 je
diferencovatelná v bodě
x∗
je
diferencovatelná v bodě
x∗ 
 n, a
nechť u
n, a
nechť u 
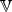 n. Pak existuje
směrová derivace fu(x∗) a platí
n. Pak existuje
směrová derivace fu(x∗) a platí

Důkaz. Nechť f je diferencovatelná v bodě x∗. Z definice směrové derivace dostáváme
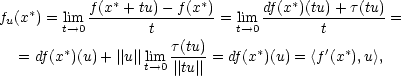
|
 0
0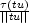 = 0. □
= 0. □
Ve
fyzikální terminologii se vektor f (x∗) nazývá gradient
funkce f v bodě
x∗ a zna
čí se gradf(x∗). Z lineární algebry
víme, že skalární součin
(x∗) nazývá gradient
funkce f v bodě
x∗ a zna
čí se gradf(x∗). Z lineární algebry
víme, že skalární součin 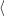 gradf(x∗),u
gradf(x∗),u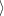 nabývá pro vektory u
dané
konstantní délky
největší hodnotu,
jestliže jsou vektory gradf(x∗) a u lineárně závislé. Protože směrová derivace
fu(x∗) udává rychlost změny funkce
f ve
směru
vektoru u, je gradf(x∗) směr, v němž funkce
f v bodě
x∗ nejrychleji roste.
Podobně −gradf(x∗) je směr, v němž funkce
nejrychleji klesá.
nabývá pro vektory u
dané
konstantní délky
největší hodnotu,
jestliže jsou vektory gradf(x∗) a u lineárně závislé. Protože směrová derivace
fu(x∗) udává rychlost změny funkce
f ve
směru
vektoru u, je gradf(x∗) směr, v němž funkce
f v bodě
x∗ nejrychleji roste.
Podobně −gradf(x∗) je směr, v němž funkce
nejrychleji klesá.
Poznámka 4.4. Diferenciál definovaný v Definici 4.1 se nazývá také totální nebo Fréchetův a lze jej definovat i pro zobrazení mezi lineárními normovanými prostory, což jsou většinou nekonečně dimenzionální prostory. Kromě toho existují jiné, obecnější diferenciály, používané často v diferenciálním počtu v normovaných lineárních prostorech, např. slabý (Gâteauxů v) diferenciál. Podrobnější informace o této problematice lze nalézt ve skriptu [N2].
V tomto odstavci zavedeme diferenciály
vyšších řádů pro funkce více proměnných. Připomeňme, že diferenciál
m-tého řádu funkce jedné
proměnné v bodě x

 je mocninná funkce m-tého stupně přírůstku h
je mocninná funkce m-tého stupně přírůstku h

Pojem diferenciálu m-tého řádu funkce n proměnných bychom mohli definovat pomocí jisté limity jako v Definici 4.1 pro diferenciál prvního řádu a pak ukázat, že z existence m-tého diferenciálu plyne existence parciálních derivací m-tého řádu, které jsou rovny jistým konstantám vystupujícím v limitním vztahu definujícím m-tý diferenciál (srovnej s Větou 4.1 pro m = 1). Podrobně je tento postup uveden ve skriptu [N2]. Zde pro jednoduchost uvedeme pouze konečný výsledek, který nejprve zformulujeme pro funkci dvou proměnných.
|
Definice 4.2. Nechť funkce f :
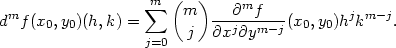
|
Poznámka 4.5. Pro případ m = 1 je vzorec pro dmf samozřejmě totožný se vztahem (4.4 ). Pro m = 2,3 dostáváme diferenciály 2. a 3. řádu

|
Pro případ n proměnných je diferenciál m-tého řádu homogenní funkce n proměnných h = (h1,…,hn)
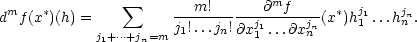
Tento vztah se často zapisuje pomocí formálního umocnění takto:

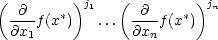
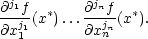
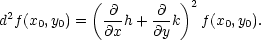
V tomto odstavci řešíme následující úlohu: Je dána dvojice funkcí dvou proměnných P(x,y),Q(x,y). Máme rozhodnout, zda existuje funkce H(x,y) taková, že

Funkce H se nazývá kmenová funkce funkcí P,Q. Odpověď na otázku existence kmenové funkce dává následující věta.
Věta 4.5. Nechť P,
Q jsou spojité funkce
proměnných x, y definované na otevřené jednoduše
souvislé1 množině Ω 
 2,
které mají na této množině spojité parciální derivace Py,
Qx. Pak výraz P(x,y)dx
+ Q(x,y)dy je
diferenciálem nějaké funkce, právě když platí
2,
které mají na této množině spojité parciální derivace Py,
Qx. Pak výraz P(x,y)dx
+ Q(x,y)dy je
diferenciálem nějaké funkce, právě když platí
![Py(x,y) = Qx(x, y) pro kaˇzdé [x,y] ∈ Ω.](diferencialni-pocet365x.png) |
(4.7) |
Důkaz.
„ “: Nechť platí (4.7) a [x0,y0]
“: Nechť platí (4.7) a [x0,y0]
 Ω
je libovolné. Položme
Ω
je libovolné. Položme
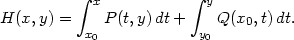
|
„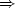 “: Je-li
výraz P dx + Qdy
diferenciálem nějaké kmenové funkce H, pak P =
Hx,Q
= Hy.
Ze spojitosti parciálních derivací Py,Qx
plyne spojitost smíšených derivací Hxy
a Hyx, které jsou si rovny (Schwarzova
věta 3.2
), a rovnost Hxy
= Hyx
je ekvivalentní rovnosti (4.7
). □
“: Je-li
výraz P dx + Qdy
diferenciálem nějaké kmenové funkce H, pak P =
Hx,Q
= Hy.
Ze spojitosti parciálních derivací Py,Qx
plyne spojitost smíšených derivací Hxy
a Hyx, které jsou si rovny (Schwarzova
věta 3.2
), a rovnost Hxy
= Hyx
je ekvivalentní rovnosti (4.7
). □
Příklad 4.3. Rozhodněte, zda výraz (x2 − y2)dx + (5 − 2xy)dy je diferenciálem nějaké funkce; v případě že ano, určete tuto (kmenovou) funkci.
Řešení. Nejprve ověříme, zda je uvedený výraz opravdu diferenciálem. Platí
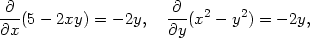
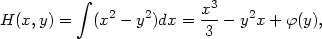
 (y) hraje
roli integrační konstanty, neboť její derivace podle x je nulová. Derivováním podle y a dosazením do vztahu Hy
= Q dostáváme
(y) hraje
roli integrační konstanty, neboť její derivace podle x je nulová. Derivováním podle y a dosazením do vztahu Hy
= Q dostáváme
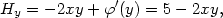

 (y) =
5, tj.
(y) =
5, tj.  (y) =
5y+c.
Vypočítali jsme, že zadaný výraz je diferenciálem funkce
(y) =
5y+c.
Vypočítali jsme, že zadaný výraz je diferenciálem funkce
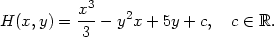
Poznámka 4.6. Pojem kmenové funkce také úzce souvisí s tzv. exaktní diferenciální rovnicí. Uvažujme diferenciální rovnici (tj. rovnici, kde neznámou je funkce y = y(x), která v rovnici vystupuje spolu se svými derivacemi)
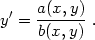 |
(4.8) |
Dosadíme-li y =
=  , dostáváme rovnici
, dostáváme rovnici


 (říkáme, že funkce y =
f(x) je
zadána implicitně, viz Kapitola 8
).
(říkáme, že funkce y =
f(x) je
zadána implicitně, viz Kapitola 8
).
Zcela
analogický problém můžeme řešit pro funkce n
proměnných. Podobně
jako v důkazu
Věty 4.5
lze
ukázat, že v případě n-tice
funkcí P1,…,Pn :  n
n

 se
spojitými parciálními derivacemi
prvního řádu je
výraz P1(x)dx1
+ ⋯
+ Pn(x)dxn
diferenciálem
jisté kmenové
funkce n proměnných v bodě
x =
[x1,…,xn], právě když
se
spojitými parciálními derivacemi
prvního řádu je
výraz P1(x)dx1
+ ⋯
+ Pn(x)dxn
diferenciálem
jisté kmenové
funkce n proměnných v bodě
x =
[x1,…,xn], právě když

Příklad 4.4. Rozhodněte, zda je výraz (y + z)dx + (x + z)dy + (x + y)dz diferenciálem jisté funkce H(x,y,z). Pokud ano, tuto funkci určete.
Řešení. Nejprve ověříme, zda je daný výraz opravdu diferenciálem:

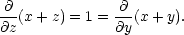

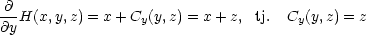
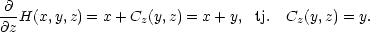

 . Zadaný
výraz je
diferenciálem funkce
. Zadaný
výraz je
diferenciálem funkce

Poznámka 4.7. Skutečnost, zda je výraz
 |
(4.9) |
diferenciálem jisté funkce, hraje fundamentální roli v teorii křivkový ch integrálů a v jejich fyzikálních aplikacích. Funkce P,Q,R můžeme chápat jako souřadnice nějakého silového pole v prostoru – vektor F(x,y,z) = (P(x,y,z),Q(x,y,z),R(x,y,z)) udává směr a velikost síly působící v bodě [x,y,z]. Toto pole se nazývá konzervativní nebo také potenciálové, jestliže se při pohybu v tomto poli po libovolné uzavřené křivce nevykoná žádná práce (tuto vlastnost má například pole gravitační). Lze ukázat, že pole F je konzervativní, právě když je výraz (4.9) diferenciálem jisté funkce H. Tato funkce se ve fyzikální terminologii nazývá potenciál silového pole.
Cvičení 
4.1. Určete diferenciál funkce v daném bodě, popř. v obecném bodě tam, kde není konkrétní bod specifikován:
a) z
= xy +
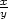 , [x0,y0] =
[1,1] , [x0,y0] =
[1,1] |
e) z =
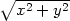 , [x0,y0] =
[3,4] , [x0,y0] =
[3,4] |
b) z =
arctg 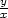 , [x0,y0] =
[1,−1] , [x0,y0] =
[1,−1] |
f) z
= arcsin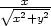 , [x0,y0] =
[1, , [x0,y0] =
[1,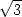 ] ] |
c) z
= arctg  , [x0,y0] =
[ , [x0,y0] =
[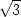 ,1] ,1] |
g) u
= 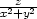 , [x0,y0,z0] =
[1,0,1] , [x0,y0,z0] =
[1,0,1] |
d) u
= x , [x0,y0,z0] =
[2,1,1] , [x0,y0,z0] =
[2,1,1] |
h) u
=   |
4.2. Pomocí diferenciálu vypočtěte přibližně:
a) arctg  |
c)  |
e) 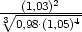 |
b) arcsin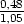 |
d) ln(0,972 + 0,052) | f) e0,053−0,02 |
4.4. Určete rovnici tečné roviny ke grafu
funkce v daném bodě:
a) f(x,y) =
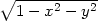 , [x0,y0,z0] =
[
, [x0,y0,z0] =
[ ,
,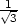 ,
, ]
]
b) f(x,y) =
x2 +
xy + 2y2, [x0,y0,z0] =
[1,1,4]
c) f(x,y) =
arctg  , [x0,y0,z0] =
[1,−1,?]
, [x0,y0,z0] =
[1,−1,?]
d) f(x,y) =
ex2+y2
, [x0,y0,z0] =
[0,0,?]
4.5. Na grafu funkce f najděte bod, v němž je tečná rovina
(nadrovina) rovnoběžná s danou rovinou (nadrovinou):
a) f(x,y) =
x3 +
y3, 
 12x
+ 3y −
z =
0
12x
+ 3y −
z =
0
b) f(x,y) =
 ,
, 
 ax +
by − z
= 0
ax +
by − z
= 0
c) f(x,y) =
x2 −
y2, 
 x +
y + z
= 0
x +
y + z
= 0
d) f(x,y) =
xy, 
 x −
z =
0
x −
z =
0
e) f(x,y,z) =
x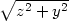 ,
, 
 x +
y − z
− u =
0
x +
y − z
− u =
0
f) f(x) =
 ,
, 
 a1x1
+ ⋯ +
anxn
+ xn+1 = 0
a1x1
+ ⋯ +
anxn
+ xn+1 = 0
4.6. Pomocí diferenciálu vypočtěte směrové
derivace funkce f ve směru
vektoru u v daném
bodě:
a) f(x,y) =
xy, u =
(1,2), [x0,y0] =
[1,1]
b) f(x,y,z) =
 ,u =
(1,0,1), [x0,y0,z0] =
[0,1,0]
,u =
(1,0,1), [x0,y0,z0] =
[0,1,0]
4.7. Vypočtěte diferenciály vyšších řádů zadaných funkcí (v obecném bodě):
| a) z = xln(xy), d2z =? | d) z = ln(x + y), dnz =? |
| b) z = x3 + y3 − 3xy(x − y), d2z =? | e) z
=  , dnz
=? , dnz
=? |
| c) z = (x2 + y2)ex+y, dnz =? | f) u = xyzex+y+z, dnu =? |
4.8. Zjistěte, zda dané výrazy jsou totálními diferenciály nějaké funkce, a pokud ano, najděte je:
a) (x
+ lny) dx +
(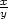 +
siny) dy +
siny) dy |
c) 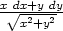 |
| b) x sin2y dx + x2 cos2y dy | d) (y2 − 1) dx + (2xy + 3y) dy |
4.9. Zjistěte, zda dané výrazy jsou totálními diferenciály nějaké funkce, a pokud ano, najděte je:
| a) (3x2 − 3xyz + 2)dx + (3y2 − 3xz + lny + 1)dy + (3z2 − 3xy + 1)dz |
b) 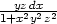 + + 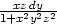 + + 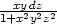 |
∗
Nikdy nepovažujte své studium za povinnost, ale za záviděníhodnou příležitost naučit se poznávat osvobozující účinky krásy ve sféře ducha, abyste z toho vy získali osobní potěšení, a společenstv í, k němuž budete později patřit, výhody. (A. Einstein)
∗
1Oblast Ω se nazývá jednoduše souvislá, jestliže libovolnou uzavřenou křivku ležící v Ω lze spojitě deformovat v Ω do bodu.
[Další] [Předchozí] [Předchozí – na konec] [Na začátek] [Výše]