10. Dědičnost kvantitativních znaků
Vzorce pro výpočet
Průměrné hodnoty:
= 
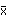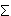xi / n
Průměrné hodnoty rozptylu:
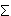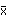s2 = (xi - )2 / n - 1
Průměrné hodnoty směrodatné odchylky:
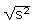
Příklad 1
U prosa byl studován počet listů na stéble. Po křížení dvou linií byly získány tyto údaje:
| Počet listů na stéble | |||||||||||||||||
| 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | N | ||
| P1 | 1 | 17 | 55 | 66 | 34 | 5 | 178 | ||||||||||
| P2 | 3 | 6 | 6 | 16 | 17 | 23 | 50 | 29 | 20 | 12 | 4 | 1 | 187 | ||||
| P2 | 5 | 5 | 28 | 51 | 58 | 27 | 5 | 179 | |||||||||
| P2 | 1 | 8 | 37 | 144 | 303 | 454 | 452 | 322 | 153 | 31 | 8 | 1913 | |||||
-
Pro každou populaci vypočtěte průměr, rozptyl, směrodatnou odchylku a 68, 95 a 99,7% intervaly spolehlivosti průměru pomocí jedno, dvou a trojnásobku odchylky.
Jaký je pravděpodobný počet genů, které determinují počet listů. Vyjděte z údajů v generaci F2.
Doplňte průměrnou hodnotu počtu listů na stéble u prosa v generaci:
P1:
P2:
F1:
F2:
(zaokrouhlete na 2 desetinná místa)
Doplňte směrodatnou odchylku počtu listů na stéble v generaci:
P1:
P2:
F1:
F2:
(zaokrouhlete na 2 desetinná místa)
Uveďte pravděpodobné rozpětí počtu genů, které se podílí na determinaci tohoto znaku:
až genů
Vzorové řešení
Generace P1:
xi = (1 x 10) + (17 x 11) + (55 x 12) + (66 x 13) + (34 x 14) + (5 x 15) = 10 + 187 + 660 + 858 + 476 + 75 = 2266
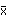= 2 266 / 178 = 12,73
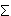(x - 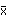)2 x počet případů = [(10 – 12,73)2 x 1] + [(11 – 12,73)2 x 17] + ............= 7,4529 + 50,8793 + 29,3095 + 4,8114 + 54,8386 + 25,7645 = 173,0562
s2 = 173,0562 / 177 = 0,98
s = 0,99
12,73 ± 0,99 <11,74;13,72>
12,73 ± 1,98 <10,75;14,71>
12,73 ± 2,97 <9,76;15,7>
Generace P2:
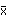= 3 315 / 187 = 17,73
s2 = 858,5894 / 186 = 4,62
s = 2,15
17,73 ± 2,15 <15,58;19,88>
17,73 ± 4,3 <13,43;22,03>
17,73 ± 6,45 <11,28;24,18>
Generace F1:
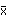= 2 580 / 179 = 14,41
s2 = 273,4099 / 178 = 1,54
s = 1,24
14,41 ± 1,24 <13,17;15,65>
14,41 ± 2,48 <11,93;16,89>
14,41 ± 3,72 <10,69;18,13>
Generace F2:
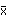= 27 762 / 1 913 = 14,51
s2 = 4 675,9713 / 1912 = 2,45
s = 1,57
14,51 ± 1,57 <12,94;16,08>
14,51 ± 3,14 <11,37;17,65>
14,51 ± 4,71 <9,8;19,22>
Odhad počtu genů provedeme z nejméně četné fenotypové skupiny v generaci F2, o níž víme, že její četnost by měla být rovna 1/4n. Nejméně četnou třídou je 9 listů na stéble a to s jedním zástupcem, tzn., že četnost je 1/1 913.
1/4n = 1/1913 —> ln4n = ln1913 —> n x ln4 = ln1913 —> n = ln1913 / ln4 = 5,45
Pokud umocníme 4n odhadovaným počtem genů, získáme číslo blízké počtu jedinců: 45 = 1024 a 46 = 4096. Počet genů, které se podílejí na determinaci tohoto znaku lze odhadnout na pět nebo šest.
Příklad 2
Vypočtěte průměr, rozptyl a směrodatnou odchylku z údajů o délce květní koruny v pokusu s tabákem.
květ tabáku
| Středy tříd (mm) | ||||||||||||||||||||
| 34 | 37 | 40 | 43 | ... | 58 | 61 | 64 | 67 | 70 | 73 | 76 | 79 | 82 | 85 | 88 | 91 | 94 | 97 | 100 | |
| P1 | 1 | 21 | 140 | 49 | ||||||||||||||||
| P2 | 13 | 45 | 91 | 19 | 1 | |||||||||||||||
| F1 | 4 | 10 | 41 | 75 | 40 | 3 | ||||||||||||||
| F2 | 1 | 5 | 16 | 23 | 18 | 62 | 3725 | 16 | 4 | 2 | 2 | |||||||||
-
Vypočtěte průměr, rozptyl a směrodatnou odchylku.
Doplňte průměrnou hodnotu délky květní koruny tabáku v generaci:
P1:
P2:
F1:
F2:
(zaokrouhlete na 2 desetinná místa)
Doplňte směrodatnou odchylku v generaci:
P1:
P2:
F1:
F2:
(zaokrouhlete na 2 desetinná místa)
Vzorové řešení
Generace P1:
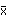= 8 308 / 211 = 39,37
s2 = 848,0259 / 210 = 4,04
s = 2,01
Generace P2:
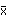= 15 736 / 169 = 93,11
s2 = 946,8649 / 168 = 5,64
s = 2,38
Generace F1:
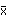= 12 029 / 173 = 69,53
s2 = 1 483,0757 / 172 = 8,62
s = 2,94
Generace F2:
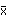= 293 752 / 3874 = 75,83
s2 = 7 443,4786 / 3 873 = 1,92
s = 1,39
tech. spolupráce: Servisní středisko pro podporu e-learningu na MU, Brno 2007