Kapitola 10
Generování grafiky v Maplu

Zde se využití počítače přímo nabízí. Tato část matematické analýzy se probírá v době, kdy nejsou probrány odpovídající partie z geometrie (zimní semestr druhého ročníku učitelského studia). Studenti proto často postrádají geometrickou představu v prostoru, a tak jsou visualizační schopnosti počítačových systémů velmi vítány.

10.1 Graf funkce dvou proměnných

Všimněme si podrobněji problematiky tvorby grafů reálné funkce dvou reálných proměnných pomocí programu Maple V. Zaměříme se zejména na případy, kdy počítačem získaný výstup (v dalším nazývaný PC-graf), neodpovídá grafu funkce (Definice 1.2 ).

Definujme funkci f(x,y) = sin(x)cos(y):
> f:=(x,y)->sin(x)*cos(y);

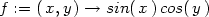
a sestrojme PC-graf funkce f (obr. 10.1 ):
> plot3d(f, -Pi..Pi, -Pi..Pi);

Stejně jednoduše je možno získat i PC-graf plochy dané parametricky, např. x = sinucosv, y = sinusinv, z = cosu, u [0, p], v [0,2p] (obr. 10.2):
> with(plots):

> plot3d([sin(u)*cos(v),sin(u)*sin(v),cos(u)],u=0..Pi,
> v=0..2*Pi,style=patch, scaling=constrained,
> axes=framed, labels=[x,y,z]);

obr. 10.2: obr. 10.3:

Parametrem scaling=constrained jsme dosáhli stejného měřítka na osách výsledného PC-grafu. Porovnejme PC-graf na obrázku 10.2 s PC-grafem na obrázku 10.3 , na kterém je tatáž koule generovaná bez použití tohoto parametru:
> plot3d([sin(u)*cos(v),sin(u)*sin(v),cos(u)],u=0..Pi,
> v=0..2*Pi,style=patch, axes=framed, labels=[x,y,z]);

Jakým způsobem probíhá konstrukce PC-grafu? Zadáme funkční předpis a množinu bodů [x,y], pro které chceme funkci zobrazit. Tato množina je typu x_min,x_maxy_min,y_max. Na ní pak program vytvoří síť, v jejichž uzlových bodech numericky spočítá funkční hodnoty (tyto jsou uloženy do objektu PLOT3D). Hustotu sítě regulujeme pomocí parametru grid=[m,n], kde m a n udává počet uzlových bodů ve směru os x a y. Implicitní nastavení tohoto parametru je [25,25]. Funkční hodnoty jsou poté podle interpolačních pravidel pospojovány a PC-graf zobrazen na výstupním zařízení.

Tento postup však zřejmě může vést k zavádějícím výsledkům. Pro ilustraci např. vytvořme PC-graf funkce g(x,y) = sin(2px)sin(2py), pro x a y z intervalu 0,25 beze změny implicitního nastavení parametrů:
> plot3d(sin(2*Pi*x)*sin(2*Pi*y), x=0..25, y=0..25,
> axes=boxed, labels=[x,y,z]);

Podrobnější analýzou zadané funkce však zjistíme, že získaný PC-graf (obr. 10.4 ) neodpovídá skutečnosti, funkce sin(2px) a sin(2py) jsou periodické s periodou 1 a tomu PC-graf na obrázku 10.4 neodpovídá. Zhuštěním sítě dostáváme výsledek bližší skutečnému chování uvažované funkce (obr. 10.5 ):
> plot3d(sin(2*Pi*x)*sin(2*Pi*y), x=0..25, y=0..25,
> axes=boxed, grid=[60,60], labels=[x,y,z]);

obr. 10.4: obr. 10.5:

Další problémy vznikají při tvorbě grafů nespojitých funkcí. Nejjednodušší situace nastává v případě, kdy studovaná funkce není v bodě [x₀,y₀] spojitá (viz Definice 2.3 ), ale v tomto bodě existuje konečná limita. Pak můžeme buď změnit hustotu uzlových bodů nebo funkci vhodným způsobem dodefinovat.

Příklad 10.1. Vytvořte PC-graf funkce

Příkazem:
> f:=(x,y)->(x^2*y)/(x^2+y^2);

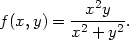
zadáme funkci a příkazem:
> plot3d(f, -3..3, -3..3, orientation=[-57,38],
> axes=framed, labels=[x,y,z]);

získáme PC-graf zobrazený na obr. 10.6 .

Bod, ve kterém vyšetřovaná funkce není spojitá, je při této hustotě sítě totožný s uzlovým bodem a program v něm nemůže spočítat funkční hodnotu. Při zobrazování na výstupním zařízení je funkční hodnota v bodě nespojitosti vynechána a zobrazený PC-graf neodpovídá v okolí bodu [0,0] grafu funkce. Všimněme si u tohoto příkladu podrobně struktury Mapleovské grafiky. Generujme graf zkoumané funkce pro x a y z  intervalu −3, 3 při hustotě sítě [7,7] a podívejme se, jaká je struktura vytvořeného objektu PLOT3D:
> p:=plot3d(f, -3..3, -3..3, orientation=[-57,38],
> axes=framed,grid=[7,7],color=black,labels=[x,y,z]);
> p;

V objektu PLOT3D jsou uloženy funkční hodnoty v uzlových bodech sítě, které jsou počítány numericky postupně po řadách. Všimněme si funkčních hodnot pro body [0,−3], [0,−2], … . Zde skutečně výpočet funkční hodnoty pro bod [0,0] „havaruje“ (FAIL). Následně je tento objekt použit při zobrazování na výstupním zařízení a chybějící funkční hodnota v bodě [0,0] je vynechána (obr. 10.7 ).

---

obr. 10.6: obr. 10.7:

---

Změníme tedy hustotu uzlových bodů tak, aby bod [0,0] (bod nespojitosti) nebyl uzlovým bodem (obr. 10.8):
> plot3d(f, -3..3, -3..3, orientation=[-57,38],
> axes=framed, grid=[30,30], labels=[x,y,z]);

Jinou možností je dodefinovat funkční hodnotu v bodě [0,0] tak, aby funkce f v tomto bodě byla spojitá. Poté generujme PC-graf získané spojité funkce:
> g:=proc(x,y) if x=0 and y=0 then 0
> else (x^2*y)/(x^2+y^2) fi end:

> plot3d(g, -3..3, -3..3, orientation=[-57,38],
> axes=framed, labels=[x,y,z]);

Obdržíme výsledek znázorněný na obr. 10.9 .

---

obr. 10.8: obr. 10.9:

---

 

Příklad 10.2. Funkce

není spojitá v bodech ležících na osách x a y, ale má zde konečnou limitu rovnu jedné.
Při pokusu o tvorbu PC-grafu příkazem:
> plot3d(sin(x*y)/(x*y), x=-3..3, y=-3..3, axes=framed,
> color=black, orientation=[150,50], labels=[x,y,z],
> tickmarks=[7,7,3]);

dostáváme PC-graf na obrázku 10.10. Zde jsou opět patrné nespojené body, ve kterých výpočet funkčních hodnot „havaroval“ (body nespojitosti na osách x a y opět vycházejí do uzlových bodů sítě).

Vytvořme tedy PC-graf spojité funkce (obr. 10.11 ) (dodefinujme funkci tak, aby byla spojitá)

> g:=proc(x,y) if x=0 or y=0 then 1
> else sin(x*y)/(x*y) fi end:

> plot3d(g, -3..3, -3..3, axes=framed,
> orientation=[150,50], color=black, labels=[x,y,z],
> tickmarks=[7,7,3]);

---

obr. 10.10: obr. 10.11:

---

Jinou možností je opět vhodně změnit hustotu sítě tak, aby body nespojitosti nebyly totožné s uzlovými body sítě.

 

Pokud v bodech nespojitosti neexistuje konečná limita, je znázornění chování takové funkce pomocí počítače obtížnější.

Příklad 10.3. Generujte PC-graf funkce f(x,y) = 1∕x.
Protože lim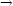_x0⁺1∕x = +, lim_x0⁻1∕x = −, není funkce f na přímce x = 0 spojitá. Příkazem:
> plot3d(1/x, x=-5..5, y=-5..5, orientation=[-63,73],
> axes=framed, labels=[x,y,z]);

dostáváme PC-graf z obr. 10.12.

---

obr. 10.12:

---

Vidíme, že PC-graf neodpovídá grafu zkoumané funkce. Podívejme se opět na objekt PLOT3D, pro zjednodušení zvolme grid=[7,3] (obr. 10.13):
> p:=plot3d(1/x, x=-5..5,y=-5..5,orientation=[-63,73],
> axes=framed,grid=[7,3],color=black,labels=[x,y,z]);p;

Maple volí rozsah zobrazovaných hodnot a měřítka na osách sám tak, aby se výsledný PC-graf co nejlépe „vešel“ na výstupní zařízení. To zejména u funkcí, jejichž limita v některém bodě je rovna , způsobuje problémy (odlišnost grafu a PC-grafu funkce). Z algoritmu realizace PC-grafu na výstupním zařízení plyne i spojení těch funkčních hodnot, které by neměly být spojeny (v okolí bodů nespojitosti, body nespojitosti v tomto případě nejsou totožné s uzlovými body). Z objektu PLOT3D je také vidět, že při této hustotě sítě a stanovené přesnosti aproximace jsou v PC-grafu potlačeny funkční hodnoty blízké +. Stačí však změnit přesnost aproximace (změnou hodnoty proměnné Digits, implicitní nastavení je Digits:=9), a dostáváme jinou síť uzlových bodů a také jiný PC-graf (obr. 10.14):
> Digits:=18;

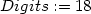
> plot3d(1/x, x=-5..5, y=-5..5, orientation=[-63,73],
> axes=framed,grid=[7,3],color=black,labels=[x,y,z]);

---

obr. 10.13: obr. 10.14:

---

Omezíme tedy rozsah zobrazovaných hodnot (view=-5..5) při původní přesnosti aproximace (obr. 10.15 ):
> Digits:=9:

> plot3d(1/x, x=-5..5, y=-5..5, view=-5..5,
> orientation=[-63,73], axes=framed, labels=[x,y,z]);

---

obr. 10.15:

---

Na PC-grafu je vidět pozitivní vliv změny rozsahu zobrazovaných hodnot, nadále však přetrvává spojování i těch bodů PC-grafu, které spojeny být neměly. Skutečnosti odpovídající PC-graf získáme následujícím způsobem. Tvorbu PC-grafu rozdělíme do dvou částí tím, že definiční obor rozdělíme na dvě oblasti: −5, − 0.001−3, 3 a 0.001, 5−3, 3. Jednotlivé samostatně vytvářené části PC-grafu v závěru interpretujeme v jediném (obr. 10.16 ) pomocí příkazu display3d z knihovny plots:
> o1:=plot3d(1/x, x=-5..-0.001, y=-3..3, view=-5..5):

> o2:=plot3d(1/x, x=0.001..5, y=-3..3, view=-5..5):

> display3d({o1,o2}, orientation=[-63,73],axes=framed,
> labels=[x,y,z]);

---

obr. 10.16:

---

 

V některých případech je vhodnější nezobrazovat funkci ve tvaru explicitním, ale provést parametrizaci funkce (x = 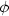(u,v), y = 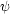(u,v), z = (u,v), kde u a v jsou parametry). Výhodné je to zejména u funkcí, které vykazují středovou nebo osovou symetrii.

Příklad 10.4. Vytvořte PC-graf funkce

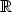Definičním oborem funkce f je množina ² −{[x,y] : x² + y² = 9}, tedy rovina xy kromě bodů ležících na kružnici se středem v bodě [0,0] a poloměrem r = 3. V těchto bodech není funkce spojitá. Pokud se pokusíme vytvořit PC-graf funkce jednoduchým příkazem:
> f:=2/(x^2+y^2-9);

> plot3d(f, x=-5..5, y=-5..5);

dostáváme obr. 10.17. Změna hustoty uzlových bodů a omezení rozsahu zobrazovaných hodnot v tomto případě nepomáhá (obr. 10.18 ):
> plot3d(f, x=-5..5, y=-5..5, view=-5..5,grid=[30,40]);

---

obr. 10.17: obr. 10.18:

---

Proveďme nyní parametrizaci x = ucosv, y = usinv, z = a generujme PC-graf (obr. 10.19 ) této funkce:
> plot3d([u*cos(v), u*sin(v), subs({x=u*cos(v),
> y=u*sin(v)}, f)], v=0..2*Pi, u=0..6, view=-5..5):

---

obr. 10.19:

---

Všimněme si rozdílu mezi PC-grafem funkce f (dané explicitně, obr. 10.17 a 10.18 ) a PC-grafem téže funkce dané parametricky (obr. 10.19 ) (graf by měl být v obou případech stejný).

Protože získaný PC-graf stále neodpovídá grafu funkce, rozdělíme tvorbu PC-grafu opět do dvou částí, přičemž parametr u bude postupně nabývat hodnot z intervalů 0, 2.999 a 3.001, 6:
> s1:=plot3d([u*cos(v), u*sin(v),
> subs({x=u*cos(v), y=u*sin(v)}, f)], v=0..2*Pi,
> u=0..2.999):

> s2:=plot3d([u*cos(v), u*sin(v),
> subs({x=u*cos(v), y=u*sin(v)}, f)], v=0..2*Pi,
> u=3.001..6):

> display3d({s1,s2}, view=-8..8);

> display3d({s1,s2}, view=-8..8, orientation=[40,102]);

Z důvodu názornosti je funkce zobrazena ze dvou různých pohledů (obr. 10.20 a obr. 10.21).

---

obr. 10.20: obr. 10.21:

---

 

Všimněme si nyní ještě některých parametrů příkazu plot3d, kterými můžeme ovlivnit vzhled výsledného PC-grafu. Doposud jsme generovali PC-graf vždy nad čtvercovou nebo obdélníkovou oblastí. Ale rozsah druhého parametru může být udán v závislosti na prvním. Například při generování PC-grafu povrchu polokoule nad čtvercovým oborem:
> plot3d(sqrt(1-x^2-y^2), x=-1..1, y=-1..1,
> scaling=constrained);

dostáváme PC-graf na obrázku 10.22. Získaný PC-graf neodpovídá na okrajích oblasti grafu funkce („zubaté okraje“ jsou opět způsobeny spojováním funkčních hodnot v uzlových bodech).

Při použití kruhové oblasti:
> plot3d(sqrt(1-x^2-y^2), x=-1..1,
> y=-sqrt(1-x^2)..sqrt(1-x^2), scaling=constrained);

(tj. proměnného rozsahu na ose y) dostáváme PC-graf odpovídající grafu funkce (obr. 10.23).

obr. 10.22: obr. 10.23:

Rozsah zobrazovaných hodnot ve směru osy z měníme volbou parametru view=[zmin..zmax]. Pokud tento parametr nezadáme, volí Maple rozsah zobrazovaných hodnot sám, což opět může vést k zavádějícím výsledkům (viz také komentář k příkladu 10.3 ). Porovnejme dva PC-grafy (obr. 10.24 a obr. 10.25), generované příkazy:
> plot3d(1/(x^2+y^2), x=-1..1, y=-1..1, axes=boxed,
> color=black, labels=[x,y,z]);

> plot3d(1/(x^2+y^2), x=-1..1, y=-1..1, view=0..6,
> style=patch, axes=boxed, labels=[x,y,z]);

obr. 10.24: obr. 10.25:

Pro zkoumanou funkci je lim_(x,y)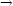(0,0)1∕(x² + y²) = +, rozsah zobrazovaných hodnot a měřítka na osách v prvním případě Maple volil sám (+ aproximoval hodnotou 7 10³¹). Výsledný PC-graf (obr. 10.24 ) pak neodpovídá grafu funkce. Obor zobrazovaných hodnot tedy omezíme parametrem view=0..6 na interval 0, 6, získaný PC-graf je znázorněn na obr. 10.25 .

10.2 Vrstevnice

Pro vytvoření představy o tvaru a průběhu znázorňované plochy nám často pomáhají vrstevnice (viz Definice 1.3 ) grafu funkce a řezy rovinami z = 0, y = 0, x = 0, příp. rovinami s nimi rovnoběžnými. Maple nám tak může pomoci při vysvětlování geometrického významu pojmu vrstevnice funkce a při jejich znázorňování.

Ukažme si nyní konstrukci vrstevnice funkce f(x,y) = x² + y² na hladině c = 6. Nejdříve generujme PC-graf funkce f a označme jej P1 (obr. 10.26 ). Poté vytvořme PC-graf roviny z = 6, označíme jej P2, a interpretujme funkci i rovinu v jednom PC-grafu (obr. 10.27 ):

obr. 10.26: obr. 10.27:

> with(plots):

> f := (x,y) -> x^2+y^2:

> P1 := plot3d(f(x,y), x=-3..3,
> y= -sqrt(9-x^2)..sqrt(9-x^2), axes=framed,
> tickmarks=[7,7,5], orientation=[45,60],
> labels=[x,y,z]): ";

> P2 := plot3d(6, x=-3..3, y= -3..3,
> style = patchnogrid):

> display3d({P1,P2}, axes=framed,tickmarks = [7,7,5],
> orientation=[45,60], labels=[x,y,z]);

Křivka, vzniklá jako průsečnice grafu funkce f a roviny z = 6 je dána parametricky rovnicemi

a představuje vrstevnici funkce f na hladině c = 6. Znázornění vrstevnice v rovině získáme průmětem do roviny xy. Situaci znázorňují následující dva obrázky (obr. 10.28 , obr. 10.29). Pro vykreslení prostorové křivky jsme použili procedury spacecurve z knihovny plots:
> P3 := spacecurve([sqrt(6)*cos(t), sqrt(6)*sin(t),6],
> t=0..2*Pi, color=black, thickness=3):

> P4 := spacecurve([sqrt(6)*cos(t), sqrt(6)*sin(t),0],
> t=0..2*Pi, color=red, thickness=3):

> display3d({P1,P2,P3},tickmarks=[7,7,5],
> orientation = [40,120], axes=boxed, labels=[x,y,z]);

> display3d({P1,P2,P3,P4},tickmarks=[7,7,5],
> orientation =[40,120], axes=boxed, labels=[x,y,z]);

obr. 10.28: obr. 10.29:

Podobným způsobem můžeme znázornit i řezy rovinami rovnoběžnými s rovinami xz a yz. Např. zobrazme průnik roviny x = 2 a grafu funkce f. Jako průsečnici získáme křivku, kterou můžeme popsat parametricky rovnicemi

> P2 := implicitplot3d(x=2,x=-3..3,y=-3..3,z=0..20,
> style=patchnogrid):

> P3 := spacecurve([2,t,j(2,t)],t=-3..3,thickness=3,
> color=black):

> display3d({P1,P2,P3},tickmarks=[7,7,5],
> axes=framed, orientation=[40,120], labels=[x,y,z]);

Pro přímé znázorňování vrstevnic používáme příkaz contourplot (obr. 10.31):
> plots[contourplot](f(x,y), x=-3..3,
> y=-sqrt(9-x^2)..sqrt(9-x^2), axes=boxed, color=black,
> contours=10, numpoints=2500, scaling=constrained,
> tickmarks=[7,7,0]);

Parametr style=patchcontour příkazu plot3d slouží k zobrazení grafu funkce s vrstevnicemi (obr. 10.32) a pro zobrazení vrstevnice na dané hladině můžeme použít příkazu levelcurve z knihovny mvcalp (obr. 10.33):
> plot3d(f(x,y), x=-3..3, y=-sqrt(9-x^2)..sqrt(9-x^2),
> style=patchcontour, axes=boxed, orientation=[40,120],
> tickmarks=[7,7,5], labels=[x,y,z]);

> with(mvcalp):

> levelcurve(f(x,y),6, x=-3..3, y=-3..3, color=black,
> scaling=constrained, tickmarks=[7,7]);

obr. 10.32: obr. 10.33:

Protože tvorba matematické grafiky není často jednoduchou záležitostí a vzhled výsledného PC-grafu můžeme ovlivňovat celou řadou parametrů, uvádíme na závěr této kapitoly i stručný přehled základních použitých příkazů a jejich parametrů. Popis všech příkazů čtenář najde buď v manuálech [C-G₁], [C-G₂] a [C-G₃] nebo přímo v systému nápovědy programu Maple V.

Přehled použitých příkazů

Generování PC-grafu funkce dvou proměnných:
plot3d(f(x,y),x=a..b,y=c..d,volby); pro výrazy a plot3d(f, a..b,c..d, volby); pro funkce.

Volitelné parametry volby ovlivňují vzhled výsledného PC-grafu. Nejčastěji používané parametry jsou popsány Tabulce 10.1 .

Generování PC-grafu funkce dvou proměnných dané parametricky (obr. 10.2 ):
plot3d([f(s,t),g(s,t),h(s,t)],s=a..b,t=c..d, volby);
K rozšíření možností práce s grafikou slouží knihovna plots. Procedury této knihovny zpřístupníme příkazem with(plots):
Vykreslení prostorové křivky (obr. 10.28 a 10.29):
spacecurve([f(t),g(t),h(t)],t=a..b,volby);
Znázornění vrstevnic (obr. 10.31 ):
contourplot(f(x,y),x=a..b,y=c..d,volby);
Znázornění vrstevnice na dané hladině (obr. 10.33):
mvcalp[levelcurve](f(x,y), hladina, x=a..b, y=c..d);
Generování PC-grafu funkce dané implicitně (obr. 10.30 a viz také Kapitola 7 ): implicitplot3d(expr1, x=a..b, y=c..d, z=p..q, volby);