Příklad 11.1. Spojité funkce mají v libovolném bodě [a,b] limitu
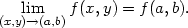
> plot3d(x-x^3-x*y^2+x^3*y^2,x=-1.4..1.4,y=-1.4..1.4,
> view=-1..1, style=patch, labels=[x,y,’z’]);
[Další] [Předchozí] [Předchozí – na konec] [Na konec] [Výše]
Počítačového systému v této kapitole využíváme zejména ke tvorbě ilustrační grafiky. Přímý výpočet limit funkce dvou proměnných není ve většině případů možný, protože neexistuje vhodný algoritmus. (Jiná situace je u funkcí jedné proměnné.) Přesto nám může být počítač nápomocen při určování limit funkce dvou proměnných a to zejména jejich transformací do polárních souřadnic a následným výpočtem limity funkce jedné proměnné.
Podobné metody lze použít při určování limit vzhledem k podmnožinám okolí limitního bodu. V této souvislosti budeme za takové podmnožiny volit spojité křivky procházející limitním bodem a mluvit o limitách závislých na cestě, resp. o limitě podél cesty.
Cyklus PC-grafů z této části je možno využít při přednáškách k ilustraci probírané problematiky a v počítačové laboratoři k samostatnému experimentování studentů. Přitom většinu zde uvedených obrázků lze bez počítače realizovat jen velmi těžko.
Příklad 11.1. Spojité funkce mají v libovolném bodě [a,b] limitu
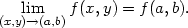
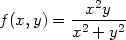
(Existence limity nezávisí na funkční hodnotě
v limitním bodě.) Aby byla funkce f v bodě [0,
0] spojitá, definujeme
f(0,0) = 0
a generujeme PC-graf vyšetřované funkce:
> f:=proc(x,y) if x=0 and y=0 then 0
> else (x^2*y)/(x^2+y^2) fi end:
> plot3d(f, -3..3, -3..3, orientation=[-57,38],
> axes=framed, style=patch, labels=[x,y,’z’]);
Následující příklady ilustrují jev, kdy hodnota limity funkce závisí na cestě, po které se k limitnímu bodu blížíme – tj. funkce nemá v daném bodě limitu.
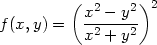
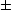 x
dostáváme
x
dostáváme
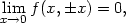
ale po osách x a y dostáváme

Protože hodnota limity závisí na cestě, po které
se k bodu [0,0]
blížíme, limita lim(x,y)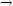 (0,0)f(x,y)
neexistuje. Uvedená situace je dobře viditelná na
obr. 11.3
.
(0,0)f(x,y)
neexistuje. Uvedená situace je dobře viditelná na
obr. 11.3
.
> f:=(x,y)->((x^2-y^2)/(x^2+y^2))^2:
> plot3d(f(x,y),x=-3..3,y=-3..3,grid=[51,49],
> axes=framed, style=patch, labels=[x,y,’z’]);
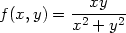
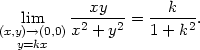
PC-grafy byly vytvořeny následující posloupností
příkazů:
> f:=(x,y)->x*y/(x^2+y^2);
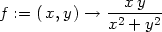
> z:=subs(x=r*cos(phi), y=r*sin(phi), f(x,y)):
> p:=plot3d([r*cos(phi),r*sin(phi),simplify(z)],r=0..1,
> phi=-Pi..Pi, grid=[15,45], axes=framed, style=patch):
> with(plots):
> display3d(p,orientation=[15,45],labels=[x,y,’z’]);
> display3d(p,orientation=[-69,38],labels=[x,y,’z’]);
![{ x2y x4+y2, [x,y] ⁄= [0,0], f (x,y) = 0, [x,y] = [0,0]](diferencialni-pocet1140x.png)
Bez použití počítače je velmi obtížné nakreslit
graf funkce a studenti často nemají s touto funkcí spojenu
konkrétní geometrickou představu (PC-graf obr. 11.6):
> f:=proc(x,y) if x=0 and y=0 then 0
> else x^2*y/(x^4+y^2) fi end:
> plot3d(f, -2..2, -2..2, grid=[100,100],
> style=patchcontour, orientation=[-46,35],
> contours=12, axes=boxed, labels=[x,y,’z’]);
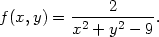
Nechť [x0,y0]
 K. Jestliže se k bodu [x0,y0] blížíme
po libovolné cestě L1
ležící vně kružnice K, pak
dostáváme
K. Jestliže se k bodu [x0,y0] blížíme
po libovolné cestě L1
ležící vně kružnice K, pak
dostáváme
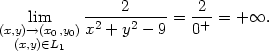
Jestliže se k bodu [0,0] blížíme po libovolné cestě L2 ležící uvnitř této kružnice, dostáváme
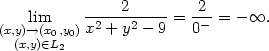
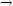 (x0,y0)f(x,y)
neexistuje. Existují pouze limity po cestách ležících uvnitř a vně
kružnice K. PC-graf funkce
f je uveden na
obrázcích 10.20
a 10.21
.
(x0,y0)f(x,y)
neexistuje. Existují pouze limity po cestách ležících uvnitř a vně
kružnice K. PC-graf funkce
f je uveden na
obrázcích 10.20
a 10.21
.
Maplu můžeme použít i při určování existence, resp. neexistence limity funkce dvou proměnných.
Následující příklady ilustrují možnosti Maplu při
procvičování některých metod určování limit funkce. Např.
u funkce dvou proměnných se k limitnímu bodu můžeme
blížit nekonečně mnoho způsoby: po přímkách, parabolách či obecných
množinách. K důkazu neexistence limity přitom stačí najít dvě
různé hodnoty limit vzhledem k různým množinám. Maple nám zde
pomáhá při výpočtu volbou y
= 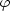 (x) (pro
vhodné
(x) (pro
vhodné 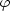 ) získaných limit funkce
jedné proměnné (př. 2.1
a př. 2.2
). Maple nám může asistovat i při
důkazu neexistence a příp. i existence limity funkce dvou
proměnných ve vlastním bodě [x0,y0]
zavedením polárních souřadnic (př. 2.3
a př. 2.4
).
) získaných limit funkce
jedné proměnné (př. 2.1
a př. 2.2
). Maple nám může asistovat i při
důkazu neexistence a příp. i existence limity funkce dvou
proměnných ve vlastním bodě [x0,y0]
zavedením polárních souřadnic (př. 2.3
a př. 2.4
).
Jinou možností řešení limit funkcí dvou proměnných je nejdříve určit graf funkce, podle grafu vyslovit hypotézu o existenci, resp. neexistenci a tuto dokázat (př. 2.5 ). K tomu lze efektivně, ale s jistou opatrností, využít PC-grafů uvažovaných funkcí.
Některé příklady z této části již byly použity v části Ilustrace, zde je však na rozdíl od předcházející části kladen důraz na výpočetní aspekt problému.
Příklad 11.8. Určete
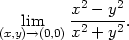
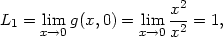
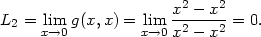
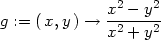
> L1:=Limit(g(x,0), x=0)=limit(g(x,0),x=0);
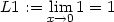
> L2:=Limit(g(x,x), x=0)=limit(g(x,x),x=0);
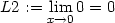
Poznámka 11.1. Pozor na nesprávné použití
Maplu při výpočtech limit!
Příkazem:
> limit(limit(g(x,y), y=0), x=0);
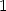
nepočítáme limitu dané funkce v bodě
[0,0], ale
pouze limitu podél osy x.
Správné použití příkazu limit
k výpočtu hledané limity je:
> limit(g(x,y), {x=0,y=0});
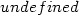
Zde tedy dostáváme, že limita neexistuje. U všech dalších příkladů uvedených v této části však Maple není přímým výpočtem schopen o existenci limity rozhodnout.
Příklad 11.9. Určete limitu funkce
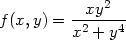
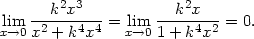
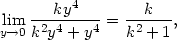
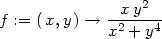
> Limit(f(x,k*x), x=0)=limit(f(x,k*x),x=0);
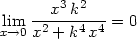
> Limit(f(k*y^2,y),y=0)=limit(f(k*y^2,y),y=0);
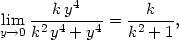
Příklad 11.10. Rozhodněte, zda existuje limita
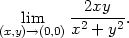
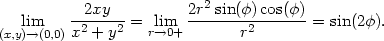
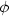 , tj. na
směru, ve kterém se blížíme k bodu [0,0],
uvedená limita neexistuje.
, tj. na
směru, ve kterém se blížíme k bodu [0,0],
uvedená limita neexistuje.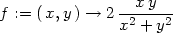
> Limit(subs(x=r*cos(phi), y=r*sin(phi), f(x,y)),
> r=0, right)= limit(simplify(subs(x=r*cos(phi),
> y=r*sin(phi), f(x,y))), r=0, right);
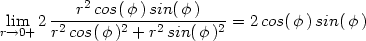
Příklad 11.11. Rozhodněte, zda existuje limita funkce
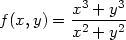
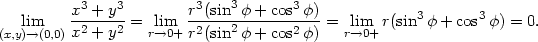
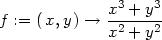
> Limit(subs(x=r*cos(phi), y=r*sin(phi), f(x,y)),
> r=0, right)= limit(simplify(subs(x=r*cos(phi),
> y=r*sin(phi), f(x,y))), r=0, right);
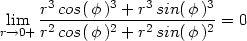
a protože funkce g(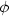 ) = sin3(
) = sin3(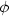 ) + cos3(
) + cos3(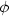 ) je ohraničená (obr. 11.7), je podle
Věty 2.6
hodnota limity rovna nule.
) je ohraničená (obr. 11.7), je podle
Věty 2.6
hodnota limity rovna nule.
Příklad 11.12. Určete
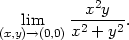
> g:=(x,y)->x^2*y/(x^2+y^2);
> plot3d(g, -0.003..0.003, -0.003..0.003,
> orientation=[-57,38], axes=framed, labels=[x,y,’z’]);
Z toho, že funkční hodnoty se „blíží“ nule, lze usoudit, že limita funkce v bodě [0,0] patrně existuje a je rovna nule. Tuto hypotézu dále podpořme výpočtem limit po přímkách y = kx a parabolách y = kx2:
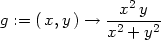
> L1:=limit(g(x,k*x), x=0);

> L2:=limit(g(x,k*x^2),x=0);

Jestliže tedy limita existuje, musí být rovna 0. Proveďme transformaci do polárních souřadnic a existenci limity ověřme podle stejné věty jako v předcházejícím příkladě:
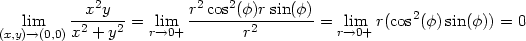
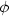 )sin(
)sin(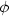 ) je ohraničená, je hodnota limity rovna
nule.
) je ohraničená, je hodnota limity rovna
nule.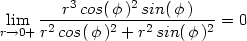
Příklad 11.13. Určete
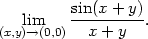
> f:=(x,y)->sin(x+y)/(x+y);x1:=0:y1:=0:
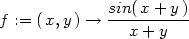
> Limit(f(x,y1+k*(x-x1)),x=x1)=
> limit(f(x,y1+k*(x-x1)),x=x1);
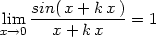
Všimněme si, že f je složená z funkcí F a G,
kde:
> F:=(x,y)->x+y;G:=t->sin(t)/t;
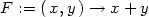
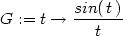
> (G@F)(x,y);
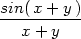
> Limit(G(t),t=0)=limit(G(t),t=0);
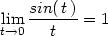
V našem případě limity funkcí F a G
existují a tedy podle věty o limitě složené funkce je limita
rovna jedné.
> plot3d(f(x,y), x=-2*Pi..2*Pi, y=-2*Pi..2*Pi,
> orientation=[162,36], axes=framed, style=patch,
> labels=[x,y,’z’], tickmarks=[7,7,3]);
Příklad 11.14. Určete
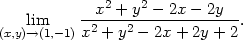
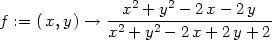
> Limit(f(x,y1+k*(x-x1)),x=x1)=
> limit(f(x,y1+k*(x-x1)),x=x1);
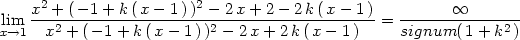
Z toho plyne, že pokud se k limitnímu
bodu blížíme po přímkách, dostáváme limitu rovnu 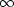 , neboť sgn(1
+ k2) = 1.
K důkazu existence limity využijeme věty o limitě součinu
funkcí:
, neboť sgn(1
+ k2) = 1.
K důkazu existence limity využijeme věty o limitě součinu
funkcí:
> Cit:=numer(f(x,y));
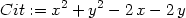
> Ijmen:=1/denom(f(x,y));
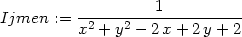
> (x-1)^2+(y-1)^2=expand((x-1)^2+(y+1)^2);
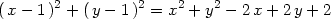
Jmenovatel denom(f(x,y)) je vždy kladný a
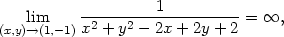
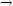 (1,−1)x2
+ y2
− 2x
− 2y
= 2 a tedy součin je roven
(1,−1)x2
+ y2
− 2x
− 2y
= 2 a tedy součin je roven
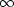 (obr. 11.10).
(obr. 11.10).
[Další] [Předchozí] [Předchozí – na konec] [Na začátek] [Výše]