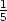 =
0 (obr. 15.1
) a plochy určené implicitně rovnicí
coshz =
=
0 (obr. 15.1
) a plochy určené implicitně rovnicí
coshz =
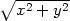 (obr. 15.2
).
(obr. 15.2
).[Další] [Předchozí] [Předchozí – na konec] [Na konec] [Výše]
V první části této kapitoly si všimneme problémů spojených s generováním PC-grafů funkce dané implicitně, v druhé pak použijeme Maplu při výpočtech derivací implicitně dané funkce.
Ke generování PC-grafu funkce dané implicitně
používáme příkazů z knihovny plots: implicitplot a
implicitplot3d. Pro ilustraci generujme
PC-grafy křivky určené implicitně rovnicí x3
+ y3
− 5xy
+ 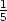 =
0 (obr. 15.1
) a plochy určené implicitně rovnicí
coshz =
=
0 (obr. 15.1
) a plochy určené implicitně rovnicí
coshz =
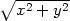 (obr. 15.2
).
(obr. 15.2
).
> with(plots):
> implicitplot(x^3+y^3-5*x*y+1/5=0, x=-3..3, y=-3..3,
> grid=[50,50]);
> implicitplot3d(cosh(z)=sqrt(x^2+y^2),x=-3..3,y=-3..3,
> z=-2..2, grid=[15,15,20], style=patchcontour,
> orientation=[30,70]);
Při generování PC-grafů křivek daných implicitně
při použití příkazu implicitplot není možno zaručit, že
PC-graf bude odpovídat grafu křivky dané implicitně. Maple má při
tvorbě PC-grafu „problémy“ s body [x,y],
ležícími na křivce F(
x,y) = 0, pro které je
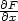 (x,y) = 0
a zároveň
(x,y) = 0
a zároveň 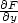 (x,y) =
0. Typickým příkladem je křivka 2x4
+ y4
− 3x2y
− 2y3
+ y2
= 0 (obr. 15.3). Platí
Fy =
4y3 −
3x2
− 6y2
+ 2y, Fy(0,0) = 0,
Fy(0,1) = 0
a Fx =
8x2 −
6xy, Fx(0,0) = 0,
Fx(0,1) = 0.
Ani zhuštění sítě v tomto případě nevede v okolí bodů
[0,0] a
[0,1]
k uspokojivým výsledkům (obr. 15.4
):
(x,y) =
0. Typickým příkladem je křivka 2x4
+ y4
− 3x2y
− 2y3
+ y2
= 0 (obr. 15.3). Platí
Fy =
4y3 −
3x2
− 6y2
+ 2y, Fy(0,0) = 0,
Fy(0,1) = 0
a Fx =
8x2 −
6xy, Fx(0,0) = 0,
Fx(0,1) = 0.
Ani zhuštění sítě v tomto případě nevede v okolí bodů
[0,0] a
[0,1]
k uspokojivým výsledkům (obr. 15.4
):
> implicitplot(2*x^4+y^4-3*x^2*y-2*y^3+y^2,
> x=-5/2..5/2, y=-5/2..5/2);
> implicitplot(2*x^4+y^4-3*x^2*y-2*y^3+y^2,
> x=-5/2..5/2, y=-5/2..5/2, grid=[100,100]);
V tomto případě je nejlepším řešením
parametrizace zkoumané křivky:
> factor(subs(x=r*cos(phi), y=r*sin(phi),
> 2*x^4+y^4-3*x^2*y-2*y^3+y^2));
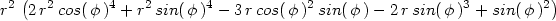
> eqn:=op(2,");
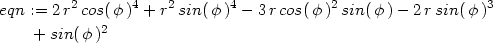
> sols:=map(unapply, sols, phi);
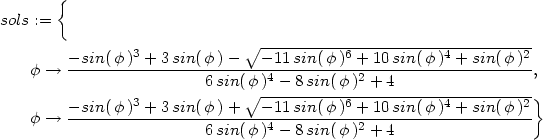
Při pokusu o generování PC-grafu pro křivku
určenou implicitně rovnicí 9x2
+ 16y2
− 24xy
− 8y
+ 6x + 1 =
0 dostáváme prázdný PC-graf a ani zhuštění sítě opět
nepomáhá. Pokusme se problém vyřešit jiným
způsobem (obr. 15.6
):
> Eq:= 9*x^2+16*y^2-24*x*y-8*y+6*x+1=0;
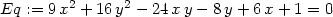
> student[completesquare](Eq, x );
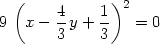
> s:=solve( ", {y} );
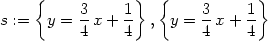
> assign(s);
> plot(y, x=-5..5, labels=[x,’y’]);
Závěrem ukažme efekt změny přesnosti
aproximativní aritmetiky a hustoty sítě na PC-graf pro křivku danou
implicitně rovnicí 1 = 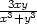 (obr. 15.7
–15.9
).
(obr. 15.7
–15.9
).
> eq:= 1=(3*x*y)/(x^3+y^3):
> implicitplot(eq,x=-4..4,y=-4..4);
Error, (in plot/iplot2d/levelcurve)
1st index, 1251, larger than upper array bound 1250
> Digits := 80:
> implicitplot(eq,x=-4..4,y=-4..4,grid=[30,30]);
> implicitplot(eq,x=-4..4,y=-4..4,grid=[40,40]);
> implicitplot(eq,x=-4..4,y=-4..4,grid=[50,50]);
Z obrázků 15.7 –15.9 je vidět, že algoritmus Maplu pro generování PC-grafu křivky dané implicitně není dostatečný pro generování PC-grafu odpovídajícího grafu takto zadané křivky.
Při výpočtu derivace funkce dané implicitně rovnicí F(x,y) = 0 pomocí počítačového systému používáme následujícího postupu. Rovnici F(x,y) = 0 derivujeme podle x a na y se díváme jako na funkci proměnné x. Pak dostáváme
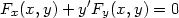
 . Stejný
postup je vhodný i při výpočtu vyšších derivací. (Postačující
podmínku pro existenci funkce zadané implicitně v okolí daného
bodu křivky udává Věta 8.1
.)
. Stejný
postup je vhodný i při výpočtu vyšších derivací. (Postačující
podmínku pro existenci funkce zadané implicitně v okolí daného
bodu křivky udává Věta 8.1
.)
Příklad 15.1. Určete rovnici tečny ke
křivce dané rovnicí y3
− xy =
−6 v bodě [7,2].
> eqn:=y(x)^3-x*y(x)=-6;
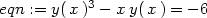
> deqn:=diff(eqn,x);
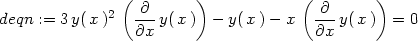
> dydx:=solve(deqn, diff(y(x), x));
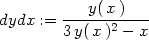
> k:=eval(subs({y=2,x=7}, dydx));
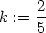
Rovnice tečny t je y
− 2
= 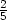 (x
− 7) tj. přímka 5y
− 2x
+ 4 = 0.
(x
− 7) tj. přímka 5y
− 2x
+ 4 = 0.
> p1:=plot(2/5*x-4/5, x=-10..10):
> p2:=implicitplot(eqn,x=-10..10,y=-4..4,grid=[50,50]):
> display({p1,p2});
Poznámka 15.1. V novějších verzích Maplu (od
verze R4) máme k dispozici proceduru implicitdiff, která počítá
derivaci funkce dané implicitně rovnicí:
> dydx:=implicitdiff(y^3-x*y, y, x);
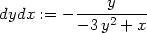
Tato procedura je však vhodná spíše pro kontrolu získaných výsledků než pro vlastní procvičování derivování funkce dané implicitně.
Vhodným cvičením do počítačové laboratoře
vyžadujícím jak znalost nezbytné teorie, tak základní znalost
programování v Maplu je: napište proceduru, která určí
derivaci funkce dané implicitně, případně její hodnotu
v zadaném bodě:
> implicitdiff := proc(g)
> local tmp,DIFFg,DIFFy,DIFFy0,p1:
> DIFFg:= diff(g,x):
> DIFFy:=
> simplify(solve(subs(diff(y(x),x)=p1,DIFFg)=0,p1));
> end:
> implicitdiff(y(x)^3-x*y(x)+6);
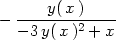
> implicitdiffb := proc(x0,y0,g)
> local tmp,DIFFg,DIFFy,DIFFy0,p1:
> tmp:=subs(y(x)=y0,g):
> if (simplify(subs(x=x0,tmp)) <> 0) then
> ERROR(‘ x0,y0 appear not to be on the curve‘):
> fi:
> DIFFg:= diff(g,x):
> DIFFy:=simplify(solve(subs(diff(y(x),x)=
> p1,DIFFg)=0,p1)):
> DIFFy0:= simplify(subs(x=x0,y(x0)=y0,DIFFy)):
> DIFFy0
> end:
> implicitdiffb(7,2,y(x)^3-x*y(x)+6);

Výstupem další uvedené procedury je přímo rovnice
tečny ke křivce dané implicitně v daném bodě a PC-graf
(obr. 15.11
):
> graf_t:=proc() local a,b,c,u,v,k;
> a:=diff(args[1],x);
> b:=diff(args[1],y);
> u:=op(1,args[2]);
> v:=op(2,args[2]);
> c:=eval(subs({x=u,y=v},args[1]));
> if c=0 then
> k:=(subs({x=u,y=v},a)*(x-u)+subs({x=u,y=v},b)*
> (y-v));
> print(‘Rovnice tečny v~bodě‘,args[2],‘je ‘,k=0);
> if nargs(graf_t)=6 then
> RETURN (plots[implicitplot]({args[1],k},
> x=args[3]..args[4],y=args[5]..args[6]));
> fi;
> fi;
> if c<>0 then
> print(‘Bod‘,args[2],‘neleží na křivce ‘,args[1]=0);
> fi;
> end;
>
> graf_t(y^3-x*y+6, [7, 2], -10,10,-4,4 );
![Rovnice tecny v bode,[7,2],je,− 2x + 4+ 5 y = 0](diferencialni-pocet1679x.png)
> graf_t(y^3-x*y+6, [1, 1]);
![Bod, [1,1],nelezi nakrivce ,y3 − x y + 6 = 0](diferencialni-pocet1681x.png)
Příklad 15.2. Rozhodněte, zda křivka x3 + y3 − 2xy = 0 leží v okolí bodu [1,1] pod tečnou nebo nad tečnou.
> alias(y=y(x));
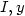
> eq:=x^3+y^3-2*x*y=0;
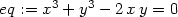
Derivujme rovnici x3
+ y3
− 2xy
= 0 podle x za předpokladu, že y je funkce proměnné x:
> diff(eq,x);
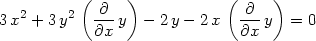
> dydx:=solve(", diff(y,x));
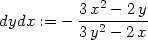
Dalším derivováním podle x obdržíme:
> diff(eq, x$2);
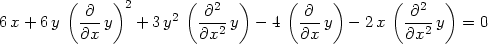
> solve(", diff(y,x$2));
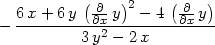
> d2ydx2:=normal(subs(diff(y,x)=dydx, "));
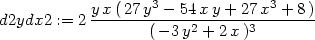
Dosazením dostaneme:
> subs({x=1,y=1}, d2ydx2);
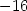
což znamená, že křivka leží v okolí bodu [1,1] pod tečnou.
Analogicky postupujeme v případě implicitně zadané funkce více proměnných.
Příklad 15.3. Určete rovnici tečné roviny
v bodě [1,0,1]
k ploše určené rovnicí x3
+ y3
+ z3
− 3xyz
− x −
y − z
= 0.
Derivujme danou rovnici podle x
a podle y, přičemž z chápeme jakožto funkci proměnných
x a y.
> alias(z=z(x,y)):
> rov:=x^3+y^3+z^3-3*x*y*z-x-y-z=0;
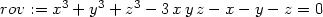
> diff(rov, x);
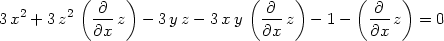
> dzdx:=solve(", diff(z,x));
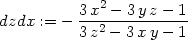
> diff(rov,y);
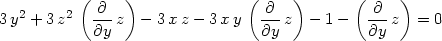
> dzdy:=solve(", diff(z,y));

Dosazením x
= 1, y = 0 a
z =
1 dostáváme:
> subs({x=1,y=0,z=1}, dzdx);
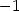
> subs({x=1,y=0,z=1}, dzdy);
Platí zx(1,0) = −1, zy(1,0) = 2 a tedy tečná rovina k dané ploše v bodě [1,0,1] má rovnici z − 1 = −(x − 1) + 2y, po úpravě x − 2y + z − 2 = 0.
Příklad 15.4. Určete lokální extrémy funkce z = f(x,y) určené implicitně rovnicí

> F:=x^2+y^2+z^2-x*z-sqrt(2)*y*z=1;
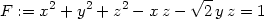
Derivováním zadávající rovnosti podle x a y
dostáváme:
> diff(F,x);
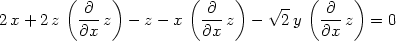
> dzdx:=solve(", diff(z,x));
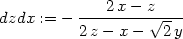
> diff(F,y);
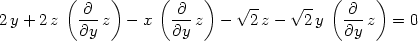
> dzdy:=solve(", diff(z,y));
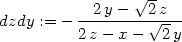
Stacionární body určíme z podmínky
zx = 0 =
zy:
> s:=solve({dzdx=0, dzdy=0, F},{x,y,z});

Vypočtěme dále parciální derivace 2. řádu ve
stacionárních bodech:
> diff(F,x,x);
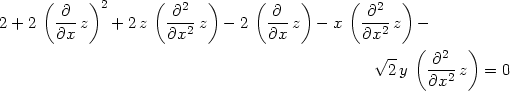
|
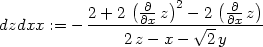
> zxxP:=subs(diff(z,x)=0, dzdxx);
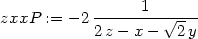
> diff(F,y,y);
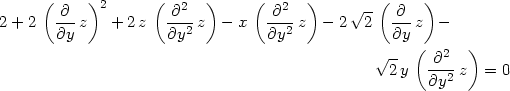
|
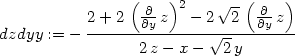
> zyyP:=subs(diff(z,y)=0, dzdyy);
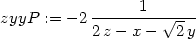
> diff(F,x,y);
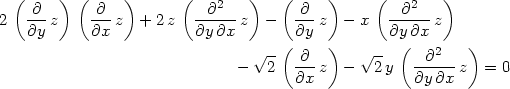
|
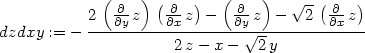
> zxyP:=subs({diff(z,y)=0,diff(z,x)=0},
dzdxy);
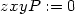
Určeme hodnotu Δ
= zxxzyy
− zxy2 ve
stacionárních bodech:
> Delta:=zxxP*zyyP-(zxyP)^2;
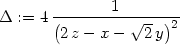
> subs(s[1], Delta);subs(s[1], zxxP);
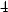
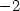
> subs(s[2], Delta);subs(s[2], zxxP);
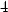
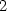
Protože v obou bodech je Δ = 4 > 0,
nastávají v těchto bodech lokální extrémy, a to maximum
v bodě [1,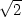 ,2]
(neboť zxx =
−2) a minimum v bodě [−1,−
,2]
(neboť zxx =
−2) a minimum v bodě [−1,−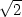 ,−2]
(zxx =
2).
,−2]
(zxx =
2).
[Další] [Předchozí] [Předchozí – na konec] [Na začátek] [Výše]