

 v bodě
x0 je limita
v bodě
x0 je limita[Další] [Předchozí] [Předchozí – na konec] [Na konec] [Výše]
Derivace funkce je druhým základním pojmem diferenciálního počtu. Cílem této kapitoly je zavést tento pojem pro funkci více proměnných a ukázat souvislost s limitou a spojitostí funkce.
Připomeňme definici a geometrický význam derivace
funkce jedné proměnné: derivace funkce f :


 v bodě
x0 je limita
v bodě
x0 je limita
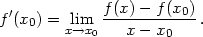 |
(3.1) |
Derivace funkce v bodě udává směrnici tečny ke křivce y = f(x) v bodě [x0,f(x0)]. Má-li funkce derivaci v bodě x0, je v tomto bodě spojitá, a tudíž zde existuje také limita funkce.
Jak jsme již ukázali v předcházející kapitole, limita funkce dvou a více proměnných je komplikovanějším pojmem než v případě funkce jedné proměnné, neboť k bodu [x0,y0] (v případě dvou proměnných) se můžeme blížit mnoha způsoby. Zcela přirozené je začít zkoumat situaci, blížíme-li se k bodu [x0,y0] ve směru souřadných os x a y. Tím se dostáváme k pojmu parciální derivace funkce dvou proměnných. Při „parciálním“1 derivování se vždy na jednu z proměnných x,y díváme jako na konstantu a podle druhé derivujeme. Blížíme-li se k bodu [x0,y0] ve směru předem daného vektoru u = (u1,u2), jde o směrovou derivaci, která je přirozeným zobecněním pojmu parciální derivace. Pro funkci n proměnných je situace analogická.
Poznámka 3.1. i) Má-li funkce z =
f(x,y)
parciální derivace ve všech bodech množiny N 
 (f), jsou
tyto derivace funkcemi proměnných x,y. Označujeme je fx(x,y),
fy(x,y),
popř.
(f), jsou
tyto derivace funkcemi proměnných x,y. Označujeme je fx(x,y),
fy(x,y),
popř.  f(x,y),
f(x,y),
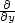 f(x,y),
f
f(x,y),
f x(x,y),
f
x(x,y),
f y(x,y),
zx, zy,
z
y(x,y),
zx, zy,
z x,
z
x,
z y.
y.
ii) Zcela analogicky se definují parciální
derivace funkce n proměnných.
Je-li z = f(x1,…,xn) funkce
n proměnných, x∗
= [x1∗,…,xn∗]

 n,
definujeme
n,
definujeme
![∂f-(x∗) = lim 1-[f(x∗1,...,x∗i− 1,x ∗i + t,x∗i+1,...,x ∗n)− f(x∗1,...,x∗n)]. ∂xi t→0 t](diferencialni-pocet215x.png)
iii) Z definice parciální derivace plyne, že při jejím výpočtu postupujeme tak, že všechny argumenty kromě toho, podle něhož derivujeme, považujeme za konstanty.
Protože parciální derivace fxi funkce n proměnných je definována jako „obyčejná“ derivace podle proměnné xi, platí pro počítání parciálních derivací obvyklá pravidla pro derivování. Uvedeme je přímo pro funkci n proměnných.
Věta 3.1. Nechť funkce f,g :
 n
n 
 mají parciální derivaci podle
proměnné xi
, i
mají parciální derivaci podle
proměnné xi
, i  {1,…,n}, na
otevřené množině M. Pak
jejich součet, rozdíl, součin a podíl má na M parciální derivaci podle xi a
platí
{1,…,n}, na
otevřené množině M. Pak
jejich součet, rozdíl, součin a podíl má na M parciální derivaci podle xi a
platí
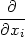 ![[f(x)± g(x)]](diferencialni-pocet217x.png) = = 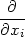 f(x) f(x)
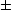 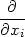 g(x), g(x), |
|||
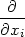 [f(x)g(x)] = [f(x)g(x)] =
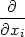 f(x)g(x) +
g(x) f(x)g(x) +
g(x)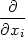 f(x), f(x), |
|||
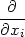 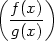 = = 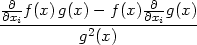 , , |
Příklad 3.1. i) Vypočtěte parciální derivace funkce dvou proměnných:
a) z
= arctg 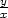 |
b) z = xy, x > 0. |
Řešení. a) Při výpočtu parciální derivace podle proměnné x považujeme proměnnou y za konstantu, tj.
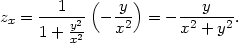
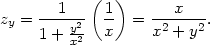
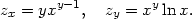
ii) Vypočtěte parciální derivace 1. řádu funkce
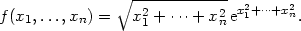
![[∘ ------------ ] -∂-- x2+ ⋅⋅⋅+ x2nex21+⋅⋅⋅+x2n = ∂xi 1 -------xi----- x21+⋅⋅⋅+x2n ∘ -2---------2 x21+⋅⋅⋅+x2n = ∘x2--+-⋅⋅⋅+-x2-e + 2xi x1 + ⋅⋅⋅+ xne = 1 n 2 2 ∘-xiex1+-⋅⋅⋅+xn--[ 2 2 ] = x2 + ⋅⋅⋅+ x2 1 + 2(x1 + ⋅⋅⋅+ x n) . 1 n](diferencialni-pocet231x.png)
|
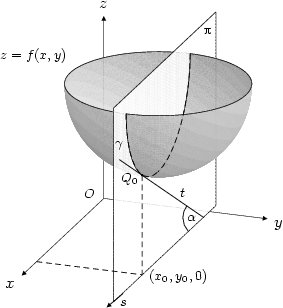
Nechť je dána funkce f :
 2
2 
 a Gf
je její graf. Nechť p je rovina
daná rovnicí y =y0.
Za rozumných předpokladů (např. spojitost funkce f) je průsečíkem Gf
a Gf
je její graf. Nechť p je rovina
daná rovnicí y =y0.
Za rozumných předpokladů (např. spojitost funkce f) je průsečíkem Gf
 p
křivka
p
křivka  v rovině p a parciální derivace fx(x0,y0) udává
směrnici tečny t k této
křivce v bodě Q0
= [x0,y0,f(x0,y0)], viz
vedlejší obrázek. (Připomeňme, že směrnice tečny t je tg
v rovině p a parciální derivace fx(x0,y0) udává
směrnici tečny t k této
křivce v bodě Q0
= [x0,y0,f(x0,y0)], viz
vedlejší obrázek. (Připomeňme, že směrnice tečny t je tg
 .)
.)
Analogicky, derivace fy(x0,y0) udává směrnici tečny ke křivce v bodě Q0, která vznikne průsečíkem plochy Gf s rovinou x = x0.
Zatímco u funkcí jedné proměnné plyne z existence derivace v daném bodě její spojitost, u funkcí více proměnných toto tvrzení neplatí.
Má-li funkce
f :  2
2

 parciální derivace
v bodě [x0,y0],
nemusí být v tomto bodě
spojitá, jak ukazuje následující příklad.
parciální derivace
v bodě [x0,y0],
nemusí být v tomto bodě
spojitá, jak ukazuje následující příklad.
Příklad 3.2. Funkce definovaná předpisem
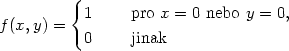
Skutečnost, že z existence parciálních derivací neplyne spojitost, je zcela přirozená Parciální derivace totiž udávají informaci pouze o chování funkce ve směrech rovnoběžných se souřadnými osami, v jiných směrech se funkce může chovat „velmi divoce“.
Obdobně definujeme parciální derivace 2. řádu fyx(x0,y0) a fyy(x0,y0).
Parciální derivace n-tého řádu (n ≥ 3) definujeme jako parciální derivace derivací (n − 1)-tého řádu.
Příklad 3.3. i) Vypočtěte derivace 2. řádu obou funkcí z Příkladu 3.1 i).
Řešení. a)
V případě funkce z
= arctg  jsme vypočetli zx
= −
jsme vypočetli zx
= −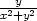 , zy
=
, zy
= 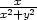 . Odtud
. Odtud
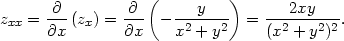
| zxy = |  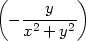 =
− =
−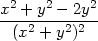 = =
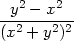 , , |
||
| zyx = | 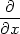 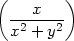 = =
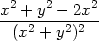 = = 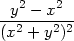 , , |
||
| zyy = | 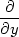 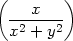 =
− =
−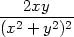 . . |
Pro funkci z = xy z části b) je zx = yxy−1, zy = xy lnx. Odtud
| zxx = | y(y − 1)xy−2, zxy = xy−1 + yxy−1 lnx, | ||
| zyx = | yxy−1 lnx
+ xy = xy−1 +
yxy−1 lnx,
zyy = xy
ln2x. = xy−1 +
yxy−1 lnx,
zyy = xy
ln2x. |
ii) Ukažte, že pro funkci u =
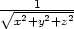 platí uxx+uyy+uzz
= 0.2
platí uxx+uyy+uzz
= 0.2
Řešení. Při výpočtu parciálních derivací využijeme skutečnost, že funkce u závisí na proměnných x,y,z symetricky. Platí
| ux = | −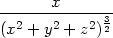 , , |
||
| uxx = | −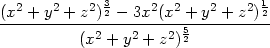 = = |
||
| = | −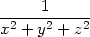 +
+ 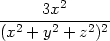 |

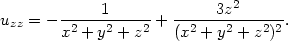
Všimněme si, že u obou funkcí v části i) předcházejícího příkladu vyšla rovnost zxy = zyx. Následující věta ukazuje, že tyto rovnosti nejsou náhodné.
Věta 3.2. (Schwarzova3) Nechť funkce f má spojité parciální derivace fxy, fyx v bodě [x0,y0]. Pak jsou tyto derivace záměnné, tj. platí
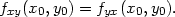 |
(3.2) |
Důkaz. Ze
spojitosti funkcí fxy
a fyx v bodě [x0,y0] plyne
existence  -okolí
-okolí  =
(x0 −
=
(x0 −
 ,x0
+
,x0
+ 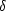 )
)
 (y0
−
(y0
− 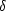 ,y0
+
,y0
+ 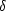 ) bodu
[x0,y0],
v němž jsou parciální derivace fxy
a fxy definovány. Pro 0 < h <
) bodu
[x0,y0],
v němž jsou parciální derivace fxy
a fxy definovány. Pro 0 < h <
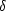 položme
položme
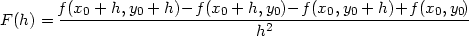 |
(3.3) |
a dále označme 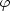 (y) =
f(x0
+ h,y)
−f(x0,y),
(y) =
f(x0
+ h,y)
−f(x0,y),
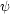 (x) =
f(x,y0
+ h)
−f(x,y0). Funkci
F pak můžeme psát ve tvaru
(x) =
f(x,y0
+ h)
−f(x,y0). Funkci
F pak můžeme psát ve tvaru
![-1- -1- F(h) = h2 [ϕ(y0 + h) − ϕ(y0)] = h2 [ψ(x0 + h) − ψ(x0)].](diferencialni-pocet261x.png)
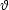 1
1
 (0,1)
takové, že
(0,1)
takové, že
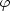 (y0
+ h)
− (y0
+ h)
− 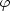 (y0) =
h (y0) =
h  (y0
+ (y0
+  1h)
= 1h)
= |
|||
=
h![[fy(x0 + h,y0 + ϑ1h) − fy(x0,y0 + ϑ1h)]](diferencialni-pocet262x.png) . . |
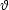 1h). Pak
g
1h). Pak
g (x) =
fyx(x,y0
+
(x) =
fyx(x,y0
+ 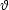 1h) a
rozdíl v poslední hranaté závorce je (opět podle Lagrangeovy
věty) g(x0
+ h)
− g(x0) =
g
1h) a
rozdíl v poslední hranaté závorce je (opět podle Lagrangeovy
věty) g(x0
+ h)
− g(x0) =
g (x0
+
(x0
+ 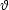 2h) =
fyx(x0
+
2h) =
fyx(x0
+ 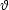 2h,y0
+
2h,y0
+ 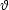 1h), kde
1h), kde
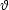 2
2  (0,1).
Dosadíme-li odtud do (3.3
), dostáváme
(0,1).
Dosadíme-li odtud do (3.3
), dostáváme
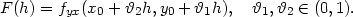
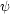 , dostáváme
, dostáváme
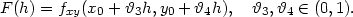
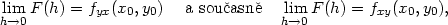
Následující příklad ukazuje, že bez předpokladu spojitosti smíšených parciálních derivací rovnost (3.2) obecně neplatí (viz příklad 12.4 ).
Příklad 3.4. Nechť funkce f je dána předpisem
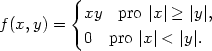
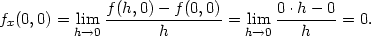
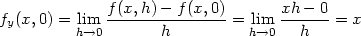
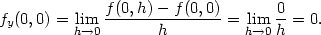
fxy(0,0) =
limh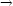 0 0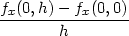 = limh = limh 00 =
0, 00 =
0, |
|||
fyx(0,0) =
limh 0 0 = limh = limh 0 0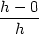 = 1. = 1. |
Matematickou indukcí můžeme tvrzení Schwarzovy věty rozšířit pro derivace vyšších řádů.
Věta 3.3. Má-li funkce f v bodě [x0,y0] a nějakém jeho okolí spojité parciální derivace až do řádu n, pak hodnota parciální derivace řádu n v libovolném bodě z tohoto okolí závisí pouze na tom, kolikrát se derivovalo podle proměnné x a kolikrát podle proměnné y, nikoliv na pořadí, v jakém se podle těchto proměnných derivovalo.
Parciá
lní derivace funkce f
v bodě
x 
 n
jsou obyčejné derivace,
které získáme zúžením
definičního oboru funkce f
na přímku jdoucí
bodem x
a rovnoběžnou s i-tou souřadnicovou osou.
Zobecněním parciálních
derivací jsou směrové derivace,
které získáme zúžením
definičního oboru funkce na
přímku
jdoucí bodem x
a mající směr
daného vektoru u
n
jsou obyčejné derivace,
které získáme zúžením
definičního oboru funkce f
na přímku jdoucí
bodem x
a rovnoběžnou s i-tou souřadnicovou osou.
Zobecněním parciálních
derivací jsou směrové derivace,
které získáme zúžením
definičního oboru funkce na
přímku
jdoucí bodem x
a mající směr
daného vektoru u

 n. To
znamená, že vyšetřujeme funkci
n. To
znamená, že vyšetřujeme funkci  (t) = f(x + tu), která je
již funkcí
jedné
proměnné, a pro ni je pojem
derivace již dobře znám.
(t) = f(x + tu), která je
již funkcí
jedné
proměnné, a pro ni je pojem
derivace již dobře znám.
Poznamenejme,
že
 n
je standardní označení pro zaměření n-rozměrného euklidovského prostoru.
n
je standardní označení pro zaměření n-rozměrného euklidovského prostoru.
Poznámka 3.2. i)
Nechť (e1,…,en) je standardní
báze v 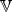 n (vektor
ei má na i-tém místě jedničku a na
ostatních místech nuly). Pak fei(x) = fxi(x), tj.
směrová derivace podle vektoru ei
je totožná s parciální derivací
podle proměnné xi
.
n (vektor
ei má na i-tém místě jedničku a na
ostatních místech nuly). Pak fei(x) = fxi(x), tj.
směrová derivace podle vektoru ei
je totožná s parciální derivací
podle proměnné xi
.
ii)
Jelikož je směrová derivace
obyčejnou derivací
funkce 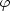 ,
platí pro počítání tato pravidla:
Nechť existuje fu,gu
v bodě
x
,
platí pro počítání tato pravidla:
Nechť existuje fu,gu
v bodě
x 
 n. Pak:
n. Pak:
a) pro
všechna c

 existuje fcu(x) a platí
fcu(x) = cfu(x)
existuje fcu(x) a platí
fcu(x) = cfu(x)
b) (f 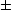 g)u(x) = fu(x)
g)u(x) = fu(x) 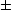 gu(x)
gu(x)
c) (fg)u(x) = fu(x)g(x) + f(x)gu(x)
d) Je-li g(x)≠0, pak
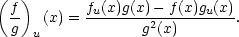
iii) Naopak neplatí aditivita směrových derivací vzhledem ke směrům. Jestliže existují fu,fv, nemusí existovat fu+v, a pokud existuje fu+v, může být fu + fv≠fu+v, viz následující příklad, část ii).
iv) V Příkladu 3.2 na straně 91
jsme
ukázali, že z existence parciálních
derivací funkce f
v bodě
[x0,y0] neplyne spojitost funkce. V části iii) následujícího příkladu ukážeme, že ani existence
směrové derivace
v bodě [x0,y0] ve směru
libovolného vektoru u

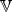 2 není postačující pro spojitost. To je
na první pohled překvapující skutečnost.
Uvědomíme-li si však, že směrové derivace
popisují chování funkce f, blížíme-li se k bodu [x0,y0] po přímkách, a definice limity
(pomocí níž je
definována spojitost v bodě [x0,y0]) zachycuje všechny způsoby „přiblížení“ (např. po
parabolách), je toto zcela přirozené.
2 není postačující pro spojitost. To je
na první pohled překvapující skutečnost.
Uvědomíme-li si však, že směrové derivace
popisují chování funkce f, blížíme-li se k bodu [x0,y0] po přímkách, a definice limity
(pomocí níž je
definována spojitost v bodě [x0,y0]) zachycuje všechny způsoby „přiblížení“ (např. po
parabolách), je toto zcela přirozené.
Příklad 3.5. i) Vypočtěte směrovou derivaci funkce f(x,y) = arctg (x2+ y2) v bodě [1,−1] ve směru vektoru u = (1,2).
Řešení. Přímým dosazením do definice a využitím l’Hospitalova pravidla dostáváme
![2 2 f(1,2)(1,1) = lim arctg[(1+-t)-+-(− 1+-2t)-]− arctg2 t→02 t lim arctg(2−-2t+-5t)-− arctg 2-= lim---−-2+-10t---- = − 2 . t→0 t t→01 + (2− 2t+ 5t2)2 5](diferencialni-pocet275x.png)
|
ii) Ukažte, že pro funkci
![{ xy(x+y) f(x,y) = x2+y2 pro (x,y) ⁄= [0,0], 0 pro (x,y) = [0,0]](diferencialni-pocet276x.png)
Řešení. Platí fu = fx, fv = fy. Protože f(t,0) = 0 = f(0,t), je fu(0,0) = 0 = fv(0,0). Pro derivaci ve směru vektoru u + v = (1,1) dostáváme z definice směrové derivace
![1 t2 ⋅2t fu+v(0,0) = ltim→0 t[f(0 + t,0+ t)− f(0,0)] = lit→m0 2t3 = 1.](diferencialni-pocet277x.png)
iii) Ukažte, že funkce f definovaná předpisem
![{ xx84+yy24, pro (x,y) ⁄= [0,0], f(x,y) = 0, pro (x,y) = [0,0]](diferencialni-pocet278x.png)

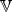 2, a
přesto
není v tomto
bodě spojitá.
2, a
přesto
není v tomto
bodě spojitá.
Řešení. Je-li 0≠u = (u1,u2) 
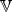 2 libovolný, podle definice
směrové derivace platí
2 libovolný, podle definice
směrové derivace platí
![1 --t4u41 ⋅t2u22- fu(0,0) = lit→m0 t[f(0+ tu1,0+ tu2)− f(0,0)] = ltim→0t(t8u81 + t4u42) = tu4u = lim -4-81-24 = 0. t→0t u1 + u2](diferencialni-pocet279x.png)
|
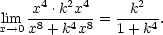
 (0,0)f(x,y) neexistuje, tedy funkce f není v bodě
[0,0] spojitá.
(0,0)f(x,y) neexistuje, tedy funkce f není v bodě
[0,0] spojitá.
Definujeme-li směrové derivace 2. řádu vztahem
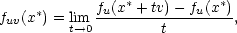
Věta 3.4. Nechť u,v

 n, funkce
f :
n, funkce
f :
 n
n

 má v bodě x∗
spojité směrové derivace
fuv a
fvu. Pak jsou si tyto
derivace rovny, tj.
má v bodě x∗
spojité směrové derivace
fuv a
fvu. Pak jsou si tyto
derivace rovny, tj.
Poznámka 3.3. Předpokládejme,
že
funkce f má v bodě x∗
spojité parciální derivace
2. řádu, a označme f
 (x∗) =
(fxixj), i,j = 1,…,n matici parciálních
derivací druhého řádu funkce
f v bodě x∗
(tato matice se někdy nazývá Hessova matice
funkce f
v bodě x∗), pak pro
libovolná u,v
(x∗) =
(fxixj), i,j = 1,…,n matici parciálních
derivací druhého řádu funkce
f v bodě x∗
(tato matice se někdy nazývá Hessova matice
funkce f
v bodě x∗), pak pro
libovolná u,v 
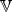 n existuje
smíšená směrová derivace
fuv(x∗) a platí
n existuje
smíšená směrová derivace
fuv(x∗) a platí
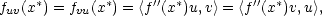
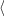 ,
,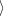 je
obvyklý skalární součin
v
je
obvyklý skalární součin
v  n.
n.
Jedním z důležitých
tvrzení diferenciálního
počtu
funkcí jedné
proměnné je Lagrangeova
věta
o střední hodnotě. Ta
říká, že pro
diferencovatelnou funkci
f :
[a,b] 
 lze rozdíl f(b) − f(a) vyjádřit ve
tvaru
lze rozdíl f(b) − f(a) vyjádřit ve
tvaru
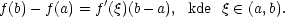
Věta 3.5. Předpokládejme, že funkce f
má
parciální derivace
fx a
fy ve
všech
bodech nějakého obdélníku M 
 2, a
nechť [x0,y0],[x1,y1]
2, a
nechť [x0,y0],[x1,y1]  M. Pak existují
čísla
M. Pak existují
čísla 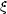 ,
,
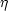 ležící mezi x0,x1, resp.
y0,y1
taková, že
ležící mezi x0,x1, resp.
y0,y1
taková, že
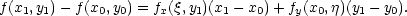
Důkaz. Platí
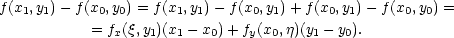
|
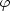 (x) = f(x,y1) a
(x) = f(x,y1) a 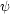 (y) = f(x0,y). □
(y) = f(x0,y). □
Poznámka 3.4. Body [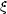 ,y1],[x0,
,y1],[x0,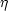 ] leží na sousedních
stranách obdélníku
určeného body [x0,y0] a [x1,y1] se stranami rovnoběžnými se souřadnými osami
(načrtněte si obrázek).
Upravíme-li si
rozdíl f(x1,y1) − f(x0,y0) poněkud odlišně, a to
] leží na sousedních
stranách obdélníku
určeného body [x0,y0] a [x1,y1] se stranami rovnoběžnými se souřadnými osami
(načrtněte si obrázek).
Upravíme-li si
rozdíl f(x1,y1) − f(x0,y0) poněkud odlišně, a to
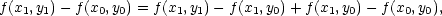
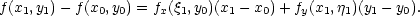
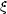 1,y0] a [x1,
1,y0] a [x1,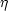 1] leží na
zbývajících dvou stranách
obdélníku.
1] leží na
zbývajících dvou stranách
obdélníku.
Projdeme-li
důkaz
Věty 3.5
, snadno
zformulujeme analogickou větu pro funkce
n proměnných. Jsou-li
x∗ = [x1∗,…,xn∗], x = [x1,…,xn] 
 n,
existují body z1,…,zn
n,
existují body z1,…,zn 
 n
ležící na hranách n-rozměrného
kvádru určeného body
x∗ a
x takové, že
n
ležící na hranách n-rozměrného
kvádru určeného body
x∗ a
x takové, že
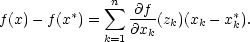
Aplikujeme-li Lagrangeovu
větu
o střední hodnotě
pro funkci jedné proměnné na funkci 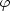 (t) = f(x + tu), dostáváme větu o přírůstku v n
ásledujícím tvaru.
(t) = f(x + tu), dostáváme větu o přírůstku v n
ásledujícím tvaru.
Věta 3.6. Nechť f :  n
n 
 má derivaci ve
směru
vektoru u
má derivaci ve
směru
vektoru u 
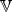 n ve
všech bodech
úsečky {x+tu;t
n ve
všech bodech
úsečky {x+tu;t  [0,1]}. Pak existuje takové číslo
[0,1]}. Pak existuje takové číslo 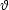
 (0,1), že
platí
(0,1), že
platí
Cvičení 
3.1. Vypočtěte parciální derivace 1. řádu funkcí:
| a) z = x3 + 2x2y + 3xy2 + 4x − 5y + 100 | h) z =
arctg 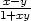 |
b) z =
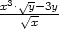 |
i) z
= 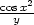 |
| c) z = xsin(x + 2y) | j) z =
ln(x
+ 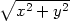 ) ) |
d) z =
sin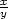  cos cos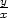 |
k) u
= ex2 (1−y−z) (1−y−z) |
e) u
= x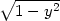 + y + y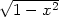 − z − z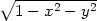 |
l) z
= arctg 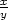 |
f) z
= e−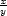 |
m) z
= arcsin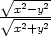 |
g) z
= ln(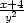 ) ) |
n) u
= ln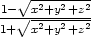 |
3.2. Vypočtěte parciální derivace 1. řádu funkcí:
| a) z = xxy | g) z =
xy  esin
pxy esin
pxy |
b) z =
2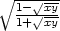 |
h) u
= x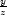 |
c) z
= ( ) )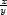 |
i) z = arctg (x − y)2 |
d) z =
xy  ln(x
+ y) ln(x
+ y) |
j) u = sin(x2 + y2 + z2) |
| e) z = (2x + y)2x+y | k) u = xyz |
f) z
= 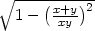 + arcsin + arcsin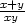 |
3.3. Vypočtěte parciální derivace 1. řádu následujících funkcí v daných bodech:
a) z
= y2
+ y  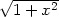 |
v [2,5] |
b) z =
ln(x
+ 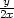 ) ) |
v [1,2] |
c) z
= 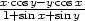 |
v [0,0] |
3.4. a) Vypočtěte uz
v bodě [0,0,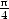 ], je-li u =
], je-li u =
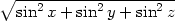 .
.
b) Vypočtěte ux + uy + uz v bodě [1,1,1], je-li u = ln(1 + x + y2 + z3).
3.6. Najděte parciální derivace 1. a 2. řádu funkcí:
| a) z = x4 + y4 − 4x2y2 | g) z = x(x+y) |
b) z =
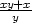 |
h) z
= ln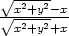 |
c) z
= 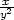 |
i) z = ln(x + y2) |
d) z =
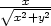 |
j) z
= ln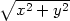 |
| e) z = xsin(x + y) | k) z
= arcsin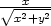 |
f) z
= 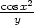 |
l) z = (1 + x2)y |
1Doslovný český překlad slova parciální je „částečný“.
2Uvedený příklad hraje důležitou roli ve fyzice; podrobněji viz příklad 5.3 ii)
3Karl Schwarz (1843–1921), německý matematik, žák K. Weierstrasse
4Joseph Louis Lagrange (1736–1813), francouzský matematik
[Další] [Předchozí] [Předchozí – na konec] [Na začátek] [Výše]