modely v zobecněném pojetí¶

kernelové vyhlazování

$$ \hat{r}(x) = \sum_{i} {y_{i}\ w(x_i,x)} $$

In [1]:

%matplotlib inline
from numpy import *
nen=30
x=r_[:10:1j*nen]+random.normal(size=nen)*0.1
y=exp(-(x-3)**2+0.1*(x-3)**3)+0.4*exp(-(x-6)**2)
y+=random.normal(size=nen)*0.1
y.max()

Out[1]:

1.0485071749517643

1 čistý a 1 asymetrický gaussovský pík
šum na úrovni 0.1

In [2]:

from matplotlib import pyplot as plt
plt.plot(x,y,'d')
fun=lambda x:exp(-(x-3)**2+0.1*(x-3)**3)+0.4*exp(-(x-6)**2)
plt.plot(r_[:10:.1],fun(r_[:10:.1]))
plt.grid()

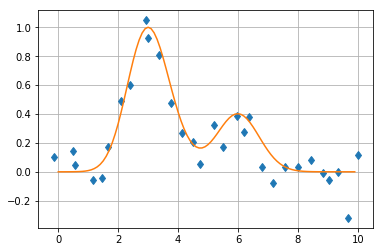
klouzavý průměr odpovídá konstantnímu kernelu

průměrování obecně

snižuje výšku píků
zvyšuje šířku
zachovává momenty - plochu pod píkem a těžiště (nultý a první mom.)

In [3]:

k=5
xf=r_[:10:100j]
vf=[]
vf8=[]
for f in xf:
    ford=argsort(abs(f-x))
    vf.append(y[ford[:5]].mean())
    vf8.append(y[ford[:8]].mean())
plt.plot(xf,vf)
plt.plot(xf,vf8)
plt.legend(["5 sousedu","8 sousedu"])
plt.ylim(-0.4,1)
plt.grid()

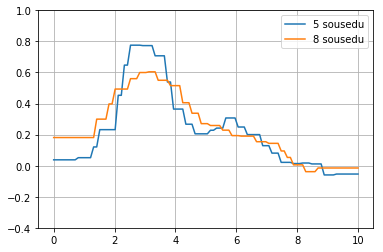
nyní zkusíme "vážené" průměrování - kernel klesající se vzdáleností od středu

In [4]:

k=5
xf=r_[:10:100j]
kf=[]
kf1=[]
kf2=[]
for f in xf:
    dist=abs(f-x)
    ford=argsort(dist)
    norm=exp(-dist[ford[:10]]**2/0.2)
    norm/=norm.sum()
    norm1=exp(-dist[ford[:10]]**2/0.4)
    norm1/=norm1.sum()
    norm2=(1-dist[ford[:10]])
    norm2[norm2<0]=0
    norm2/=norm2.sum()
    kf.append((y[ford[:10]]*norm).sum())
    kf1.append((y[ford[:10]]*norm1).sum())
    kf2.append((y[ford[:10]]*norm2).sum())
    #vf8.append(y[ford[:8]].mean())
plt.plot(xf,kf)
plt.plot(xf,kf1)
plt.plot(xf,kf2)
plt.legend(["gauss 0.1","gauss 0.2","triangl"])
plt.ylim(-0.4,1)
plt.grid()

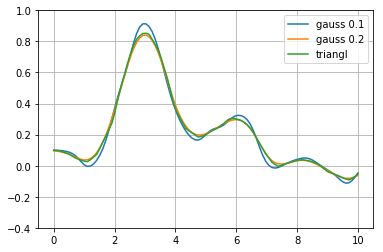
průměrování po skupinách¶

In [5]:

ymid=y.reshape(10,3).mean(1)
ystd=y.reshape(10,3).std(1)/sqrt(3)
xmid=x.reshape(10,3).mean(1)
xstd=x.reshape(10,3).std(1)/sqrt(3)

ymid2=y.reshape(6,5).mean(1)
ystd2=y.reshape(6,5).std(1)/sqrt(5)
xmid2=x.reshape(6,5).mean(1)
xstd2=x.reshape(6,5).std(1)/sqrt(5)

plt.errorbar(xmid,ymid,ystd,xstd)
plt.errorbar(xmid2,ymid2,ystd2,xstd2)

Out[5]:

<Container object of 3 artists>

fitovani analytickymi (parametrickymi) funkcemi¶

In [6]:

fun2=lambda p:p[0]+p[1]*exp(-(xc-3)**2)+p[2]*exp(-(xc-6)**2)
fun3=lambda p:p[0]+p[1]*exp(-(xc-3)**2+0.1*(xc-3)**3)+p[2]*exp(-(xc-6)**2)
fun3x=lambda p:p[0]+p[1]*exp(-(xc-3)**2+p[3]*(xc-3)**3)+p[2]*exp(-(xc-6)**2)
mat2=array([ones(x.shape),exp(-(x-3)**2),exp(-(x-6)**2)])
mat3=array([ones(x.shape),exp(-(x-3)**2+0.1*(x-3)**3),exp(-(x-6)**2)])

model 2: 2 symetrické píky
model 3: správná asymetrie 1. píku

In [7]:

#reseni pro oba modely
dcov2=linalg.inv(mat2.dot(mat2.T)) #hessian
dcov3=linalg.inv(mat3.dot(mat3.T))
dcov2.dot(mat2.dot(y)),dcov3.dot(mat3.dot(y))

Out[7]:

(array([-0.01228823,  0.96550222,  0.34427082]),
 array([-0.01208853,  0.96378374,  0.33675906]))

In [8]:

pars2,pars3=dcov2.dot(mat2.dot(y)),dcov3.dot(mat3.dot(y))
plt.plot(x,y,'d')
xc=r_[:10:0.1]
plt.plot(xc,fun2(pars2))
plt.plot(xc,fun3(pars3))
plt.grid()

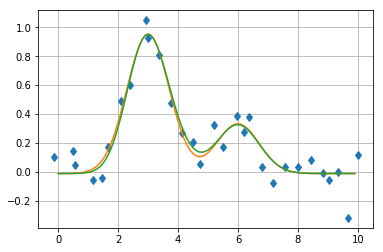
porovnání s nelineární optimalizací

In [9]:

from scipy import optimize
xc=x
minpars2=optimize.fmin(lambda p:((y-fun2(p))**2).sum(),[0,1,1])
minpars3=optimize.fmin(lambda p:((y-fun3(p))**2).sum(),[0,1,1])
pars2-minpars2,pars3-minpars3

Optimization terminated successfully.
         Current function value: 0.302759
         Iterations: 91
         Function evaluations: 158
Optimization terminated successfully.
         Current function value: 0.301742
         Iterations: 98
         Function evaluations: 175

Out[9]:

(array([  1.06920488e-05,   1.93059657e-05,  -1.33197154e-05]),
 array([ -6.39490172e-06,  -3.36273035e-05,   1.12208883e-05]))

In [10]:

minpars3x=optimize.fmin(lambda p:((y-fun3x(p))**2).sum(),[0,1,1,.3])
minpars3x,minpars3x[:3]-minpars3

Optimization terminated successfully.
         Current function value: 0.300148
         Iterations: 222
         Function evaluations: 378

Out[10]:

(array([-0.01191005,  0.96497139,  0.34055406,  0.05673663]),
 array([ 0.00017208,  0.00115403,  0.00380622]))

In [11]:

#skutecne reziduum
((y-fun(x))**2).sum()

Out[11]:

0.34015759348399499

bez konstatního členu¶

In [13]:

mat1=array([exp(-(x-3)**2),exp(-(x-6)**2)])
dcov1=linalg.inv(mat1.dot(mat1.T))
pars1=dcov1.dot(mat1.dot(y))
pars2=dcov2.dot(mat2.dot(y))
print(pars1,((y-mat1.T.dot(pars1))**2).sum())
print(pars2,((y-mat2.T.dot(pars2))**2).sum())

[ 0.94889603  0.32775809] 0.305118069645
[-0.01228823  0.96550222  0.34427082] 0.302758999292

In [14]:

sqrt(dcov2.diagonal()),sqrt(dcov1.diagonal())

Out[14]:

(array([ 0.25299914,  0.61044248,  0.60855514]),
 array([ 0.50571148,  0.50473318]))

další parametry¶

In [18]:

fun5=lambda p:p[0]+p[1]*exp(-(xc-p[3])**2+0.1*(xc-p[4])**3)+p[2]*exp(-(xc-6)**2)
minpars5=optimize.fmin(lambda p:((y-fun5(p))**2).sum(),[0,1,1,3,6])
minpars5

Optimization terminated successfully.
         Current function value: 0.294435
         Iterations: 579
         Function evaluations: 932

Out[18]:

array([-0.00929389,  0.97365716,  0.33717848,  2.95119721,  3.13620186])

In [27]:

min10,cov10=optimize.curve_fit(lambda xc,a0,a1,a2,p1,p2:fun5([a0,a1,a2,p1,p2]),xc,y,minpars5)
import numpy as np
err=np.sqrt(covmat10.diagonal())
print(err)
cov10/err[:,np.newaxis]/err[np.newaxis,:]

[ 0.03036048  0.07105162  0.06684098  0.06724396  0.60992758]

Out[27]:

array([[ 1.        , -0.32254521, -0.56428318, -0.15016285,  0.43564564],
       [-0.32254521,  1.        ,  0.2249496 , -0.19307237,  0.33412667],
       [-0.56428318,  0.2249496 ,  1.        ,  0.01861413, -0.163825  ],
       [-0.15016285, -0.19307237,  0.01861413,  1.        , -0.33892915],
       [ 0.43564564,  0.33412667, -0.163825  , -0.33892915,  1.        ]])