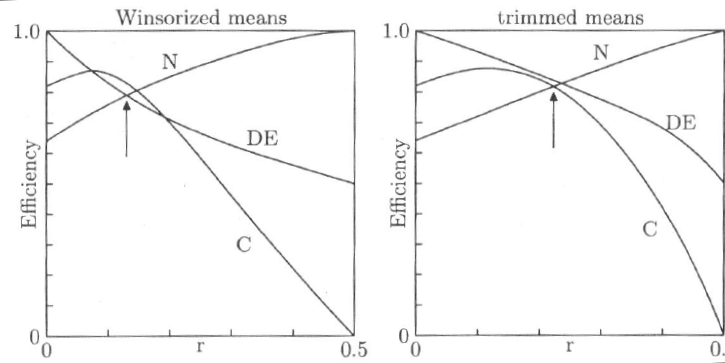
Robustní metody¶
problém odlehlých hodnot
M-odhady - pomocí vhodné váhové funkce je menší citlivost na vychýlené body než u nejm. čtverců ($d^2$)
minimalizujeme $\sum g(x_i,\theta)$, ve většině případů lze derivovat podle odhadu $\theta$: $\psi(x_i,\theta)=\partial g(x_i,\theta)/\partial \theta$ a váha se vyjádří jako
$$w(r_i)=\frac{\psi(r_i)}{r_i}$$ kde $r_i=x_i-\theta$