Metoda hlavních komponent - principal component analysis (PCA)¶
Základní otázky otázka potřebnosti dalšího parametru - jaký nejmenší počet proměnných vysvětluje dostatečně data?
Matice $A$ popisuje transformaci (rotaci/inverzi) měřených veličin $$Y=A X$$
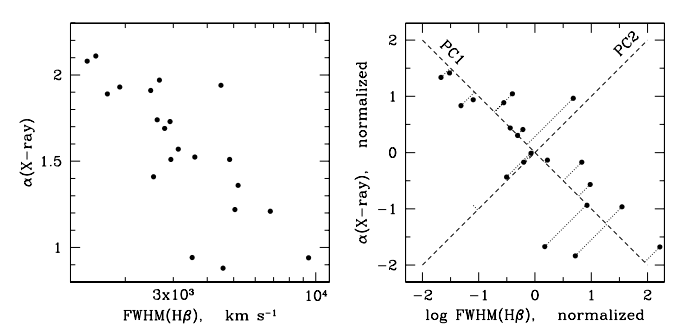
- hledáme takovou kombinaci $a_1 X$, kdy $V(a_1 X)$ bude největší za vhodné normalizační podmínky $a_1^T a_1=1$ → první hlavní komponenta
- pak hledáme takovou kombinaci $a_2 X$ , kdy $V(a_2 X)$ bude největší za podmínky $a_2^T a_2=1$ a $Cov(a_1 X, a_2 X)=0$ → druhá hlavní komponenta
- pokračujeme dále vždy ve zbývajícím prostoru kolmém na předchozí komponenty
Proměnné $X$ (jednotlivé vektory) mají kovarianční matici $\Sigma$
Praktické řešení: najdeme vlastní čísla $\lambda_i$ a vlastní vektory $\pi_i$ kovar. matice, předpokládáme, že budou ortogonální (autom. splněno, pokud jsou vlastní čísla různá).
Matice $W$ vlastních vektorů matice $X^T X$ a sdružená matice $V$ vlastních vektorů matice $X X^T$ (ident. v případě čtvercové matice X) jsou transformačními maticemi singulární dekompozice matice X ve tvaru $X=W L V$, kde L je matice pouze s diagonálními nezápornými elementy.
Stopa kovar. matice je při transformaci zachována - součet variancí je součtem vlastních čísel. Vlastní vektory obvykle uspořádáme podle velikosti vlast. čísel.
Reference:¶
[Francis] Paul J. Francis, Beverley J. Wills http://arxiv.org/abs/astro-ph/9905079 + code ref.