Kinematics

It is important for us to describe rotary motion because majority of human motions results from the rotary motion of individual segments of human body about joints as axes.

Hammer throw is a typical example of rotary motion. How is it possible to throw a hammer weighing 7,265 kg into the distance of 86,74 m (which is the world record made by Yurij Sedych from the Soviet Union at a track and field event in Stuttgart on 30 August 1986)? How did Yurij Sedych use rotary motion to throw the hammer that far? Considering that the shot used in shot put has the same weight of 7,265 kg as the hammer and the world record in shot put, made by the American Randy Barnes at a track and field event in Westwood on 20 May 1990, is „only“ 23,12 m?

Angle and Angular Displacement

Angles express mutual orientation of lines, planes, or a line and a plane. For example the axis of shin and the axis of thigh represent two intersecting lines. The mutual orientation of these two lines can be expressed by an angle. We often need to know the angle between individual body segments to describe, evaluate, and improve skills in physical exercise and sport (Fig. 10).

Figure 10 Intersecting axes of shin and thigh during squat and leap upward produce an angle.

Angle and Position

If one of the lines or planes is in a fixed position with respect to the ground, the mutual position of lines or planes is called absolute angle. For example the angle between shin and a fixed horizontal plane is an absolute angle. If both lines, or planes, move relative to each other, we are talking about relative angles (Fig. 10). Angles measured in individual joints of human body are angles that describe the relative mutual position of individual parts of human body. Angles (planar angles) are measured in radians (rad). It holds true that a planar angle, which is at the same time a plane, has the size 2π rad. Mathematically an angle can be defined as:

where φ is planar angle (rad)²⁷, l is the length of a circular arc, centred at the vertex of the angle²⁸ (m) and r is the radius of the circle (m).

Angular Displacement

Angular displacement is used to express the extent of motion in individual joints of human body. Angular displacement is the change of the absolute angle between the initial and the final position of a given segment of human body. In biomechanics we usually describe angular displacement between individual segments of human body. We can imagine a single point on each segment, connected by a ray with the intersection of these two segments (i.e. the joint). Change of mutual orientation of these rays equals angular displacement.

---

Angular displacement is the change of the absolute angle between the initial and the final position of a given segment of human body.

---

Angular displacement is a vector and its vector line lies in the axis of rotation with counter clockwise direction. We can also use the right-hand rule: if the thumb of our right hand shows the correct direction of angular displacement vector in the axis of rotation, the fingers show positive direction of rotation. Therefore we always try first to identify the plane of motion and the axis of rotation. The axis of rotation is always perpendicular to the plane on which the motion takes place. For example knee flexion (Fig. 10) takes place in sagittal plane and transversal axis. How then is angular displacement measured? Let us try to measure the extent of knee flexion. At the beginning of the measurement the initial position of shank in relation to the vertical axis is 5°. In the lowest squat position the position of shank in relation to the vertical axis is 45°. Angular displacement Δφ is then calculated as:

where φ_final is the final angle of shank in relation to the vertical axis (rad) and φ_initial is the initial angle of shank in relation to the vertical axis.

During handspring in gymnastics we have to carry out a wrist motion in large enough extent to give maximum vertical velocity to our body. The number of turns in somersaults that we can see in gymnastics, freestyle skiing, or diving, is a measure of angular displacement and is a very important criterion for the overall result in a given sport. Backward swings in certain gymnastics elements, such as roll into swing, must be described with the angle of backward swing. Iron cross in gymnastics is also assessed with the use of angular displacement. Angular displacement of a swing in football, tennis, golf, etc. has a substantial influence on the resulting stroke into a projectile.

Angular displacement, distance and displacement

When we use ice hockey sticks, tennis rackets, golf clubs, etc., we make longer otherwise short distances our arms would have travelled without using these instruments. Try to imagine elbow flexion when lifting a weight: our hand travels about ten times longer distance than the insertion of our biceps brachii. Distance travelled l of any point of a rotating body is in direct proportion to the angular displacement Δφ and the radius of the circle r along which the motion takes place²⁹:

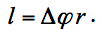
The fact that insertions of our muscles are very near to the axes of our joints brings an important benefit, as it is becoming clear now. Muscles can thus contract over shorter distance to effect longer distances of motion of our extremities. The length of muscle contraction is limited to 50 % of their original rest length. For this reason extremities’ motions would be increasingly limited with the growing distance between the axis of rotation and the muscles insertion.

Angular Velocity

Mean angular velocity ω (rad/s) is calculated as the change to angular displacement Δφ from its initial φ_initial to final φ_final value over time Δt during which the change occurred:

Angular velocity is a vector quantity and its direction is specified by the right-hand rule. The SI unit of angular velocity is radian per second (rad/s).

If, however, we are interested to know how fast a body rotates at a certain instant, we describe this by instantaneous angular velocity. With the help of mean angular velocity of a tennis racket stroke we can calculate whether a tennis player is going to hit the ball. Instantaneous angular velocity of a tennis racket at the moment of a stroke (i.e. contact with the ball) determines the following velocity of the ball. In sports such as gymnastics the more important factor of performance is mean angular velocity because it determines how many somersaults and twists the given athlete can manage.

---

Angular velocity is a ratio of the change of angular displacement and the time during which the change occurred.

---

Relation between angular velocity and peripheral velocity

In tennis, golf, hockey, and other sport events the instruments used make our arms longer. If, in these sport events, we tried to toss the projectile using only our arms, we would never achieve such velocity as we do after strokes with a hockey stick, tennis racket, golf club, etc.

---

The magnitude of peripheral velocity of any point on a rotating body equals the product of angular velocity of that body and the radius of the circle along which that point is moving.

---

where v (m/s) is the magnitude of peripheral velocity³⁰ of any point of the body rotating along a circle (e.g. velocity of the hockey stick blade at the moment of contact with the puck), ω (rad/s) is the instantaneous angular velocity, and r (m) is the radius of the circle.

Velocity of a point lying further from the axis of rotation is higher than that of points lying nearer to the axis. Angular velocity of all points of a given body is the same, however. For example longer golf clubs are used for driving with higher initial velocity to longer distances. Shorter golf clubs are used for shorter distances. If we hold a tennis racket at the very end of its handle, we can produce the highest peripheral velocity of its functional end and thus the highest initial velocity of the ball after the stroke.

In the above mentioned sports there is an important concept of effective radius. Effective radius is achieved not only with the length of athlete’s arm and the length of an instrument but also with the overall technique of the stroke execution.

The relation between peripheral and angular velocity provides us with a theoretical basis of understanding why the specific arrangement of human muscles and their insertions, in relation to the axis of rotation in given human joints, gives us such an advantage. For example our feet move much faster than is the speed of muscle contraction in those muscles that control the motion of legs in walking and running.

Angular Acceleration

---

Angular acceleration is the rate of change of angular velocity over time.

---

Mathematically we can define mean angular acceleration as:

where ε³¹ (rad/s²) is mean angular acceleration (rad/s²), Δω is the change of angular velocity(rad/s), Δt (s) is the time during which the change of angular velocity Δω occurred, ω_final (rad/s) is the angular velocity at the end of the studied process, and ω_initial (rad/s) is the angular velocity at the beginning of the studied process. Angular acceleration is measured in radians per second squared (rad/s²).

---

Angular acceleration is generated when the speed of rotation of a body increases or decreases, or if the axis of rotation changes its orientation.

---

Angular acceleration, Tangential acceleration, Centripetal acceleration

If the magnitude of angular velocity ω grows, peripheral velocity v also grows. It implies that there is a relation between angular acceleration ε and tangential acceleration a_t.

Tangential acceleration

Acceleration of any point of a rotating body can be resolved into two perpendicular components: tangential and centripetal. The tangential component (the tangent to the circular trajectory of a given point) is called tangential acceleration a_t. The magnitudes of tangential acceleration and angular acceleration are interrelated:

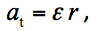
where a_t (m/s²) is the magnitude of tangential acceleration, ε (rad/s²) is the magnitude of angular acceleration, and r (m) is the radius of the circumscribed circle.

---

Tangential acceleration is a component of acceleration and it has the direction of the tangent to the circular trajectory.

---

Centripetal acceleration

Even if a body rotates with a constant angular velocity, non-zero acceleration results. This acceleration is related to the change in the direction of peripheral velocity of any point of a rotating body and it is called centripetal acceleration a_d³². If we imagine what force we have to exert in order to change the direction of a carving turn in downhill skiing, we can realize the direction of centripetal acceleration. Our lean, as well as the forces that incurvate the trajectory of our downhill motion, are directed towards the centre of our ski turns. According to the Newton’s second law, centripetal acceleration appertained to these forces is also directed towards the centre of our ski turns. Mathematically the magnitude of centripetal acceleration can be defined as:

or also

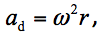
where a_d (m/s²) is the magnitude of centripetal acceleration, v_t (m/s) is the magnitude of tangential velocity of a point of the rotating body, r (m) is the radius of the circumscribed circle, and ω (rad/s) is angular velocity.

---

Centripetal acceleration is a component of acceleration and it is directed towards the centre of the trajectory’s curvature, perpendicularly to the axis of rotation.

---

The magnitude of centripetal acceleration of any point of a rotating body is directly proportional to the square of angular velocity and the radius of trajectory. If, for example, we are running in the first track, we have to exert greater centripetal force and thus accelerate towards the centre more than if we are running in the last track. For this reason the friction between track shoes and the surface is greater if we are running in the first track. In this case our tangential velocity is the same, only the radius of the trajectory is different. For thinking about centripetal acceleration we used the equation because our tangential velocity is the same in both cases.

Let us imagine a hockey player with two hockey sticks of various lengths. Both sticks have approximately the same weight but their length is different. What force must the hockey player exert with these two different sticks during a slap shot, if he keeps the same angular velocity? In this case we will calculate centripetal acceleration with the use of the equation 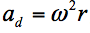because the player’s tangential velocity is the same in both cases. The player must exert greater force and greater centripetal acceleration when using the longer stick (r in this case is the perpendicular distance of the stick’s centre of gravity from the axis of rotation). We must realize, however, that even though the longer stick is better for shooting with higher initial velocity, the player must exert greater force to achieve that velocity compared to using the shorter stick. If the stick is too long, the player might not even be able to achieve sufficient velocity of the shot.

²⁷ In physical education we mostly measure angles in degrees (°).Zpět

²⁸ Vertex of an angle is defined as the starting point of rays.Zpět

²⁹ If angular distance is measured in rad.Zpět

³⁰ Vector of peripheral velocity has the direction of a tangent to the trajectory at a given point.Zpět

³¹ In literature angular acceleraton is also denoted by the Greek letter alpha α.Zpět

³² Centripetal acceleration points towards the centre of the trajectory’s curvature.Zpět