Chyby měření

Při práci s laboratorním sklem se snažíme měřit „správnou“ hodnotu měřené veličiny. Což se nám samozřejmě nepodaří úplně přesně, protože při každém měření se dopouštíme chyb různého typu. Výsledek neovlivňují pouze vlastnosti měřících pomůcek, ale také zvolená metoda měření, či samotná osoba. Vždy má tedy smysl hovořit o přesnosti měření, tj. do jaké míry naše měření odpovídá skutečnosti. Pokud bychom si přesnost měření nestanovili, měření by postrádalo smysl. Jelikož bychom jej nemohli porovnat s ostatními výsledky. Součástí každého měření je tedy důkladná analýza všech chyb, které se při něm uplatnily.

Chyby měření dělíme do několika kategorií, podle různých hledisek:

1. Podle původu (chyby osobní a chyby měřicích přístrojů, metody)
2. Podle charakteru (chyby náhodné a chyby soustavné)
3. Podle analytického vyjádření (chyby absolutní a relativní).

Někdy se uvádí také chyba krajní (mezní), což je maximální chyba měření, ke které může za daných podmínek dojít, nebo chyba větší než maximální – tzv. chyba nadměrná (hrubá).

Hrubé chyby vznikají omylem, nepozorností, únavou, špatnými podmínkami pro měření nebo špatnou volbou měřicí metody a měřicích přístrojů. Jsou snadno rozeznatelné, jelikož se nápadně liší od obvyklých hodnot téže naměřené veličiny.

Velkým problémem jsou chyby soustavné, a to z hlediska posuzování přesnosti měření, jelikož jejich původ a velikost se většinou dá určit velmi obtížně. V praxi se vyskytují s chybami náhodnými.
Soustavnou chybou měření se rozumí chyba, jejíž hodnota se nemění, opakuje-li se měření za stejných podmínek (což není vždy splněno).

Zdrojů může být hned několik, a to měřicí metody, používané měřicí přístroje, nebo osoby provádějících měření. Pečlivým rozborem měření lze soustavné chyby odhalit a také můžeme odhadnout jejich velikost a znaménko, případně je odstranit. Kdežto u náhodných chyb nedovedeme přesně pospat příčiny vzniku. I když nebudeme ve cvičení úlohu opakovat, můžeme svoje zkušenosti a poznatky uplatnit u jiné úlohy, kde je použita stejná metoda měření, popřípadě stejné měřicí přístroje.

Soustavné chyby tedy můžeme částečně eliminovat alespoň opakovaným měřením různými metodami. Soustavné chyby pak charakterizujeme jako proměnlivé se souměrným rozložením. Po vyhodnocení získáme přesnější hodnotu měřené veličiny. Může ale nastat situace, že rozptyl takto získaných hodnot bude velký, proto vyjádříme pouze rozpětí, ve kterém leží měřená veličina intervalem <X_min,X_max>.

Mnohé materiály mění delším manipulováním s nimi svoje vlastnosti, a to může způsobit další chyby v našem měření. Nebo měření nepřesníme sami například opožděním při měření času nebo chybným odečítáním hodnot ze stupnice. I měřicí přístroje jsou častými původci soustavných chyb, u kterých může být špatně nanesená stupnice nebo špatné nastavení jako je třeba citlivost či kalibrace na nulu. Je tedy velmi obtížné soustavné chyby stanovit a opravit výsledek měření. V takovém případě určíme nebo alespoň odhadneme interval, ve kterém s jistotou leží chyba jednoho měření. Výsledek měření zapíšeme ve tvaru:

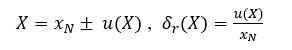
kde x_N je naměřená hodnota veličiny X, u(X) je mezní chyba měřidla v absolutním tvaru a δ_r(X) je relativní chyba výsledku.

Náhodné chyby

I když opakujeme měření s dostatečnou rozlišovací schopností, pak i při konstantní hodnotě měřené veličiny dostaneme výsledky, které se navzájem liší. Což je způsobeno řadou náhodně se kombinujících nepostižitelných vlivů, které tak způsobují náhodné chyby měření. Bohužel není možné se tomuto druhu chyb vyhnout, dokonce vznikají tím víc, čím přesnější měření provádíme.

S pomocí pravděpodobnosti a statistiky můžeme určit tu hodnotu, která je s největší pravděpodobností skutečnou (pravou) hodnotou naší veličiny. Provedeme-li velmi mnoho měření (a ,,velmi mnoho‘‘ znamená n → ∞) zjistíme, že nejvíce hodnot leží na číselné ose v okolí hodnoty, kterou nazývám střední hodnota µ. Většina veličin, které měříme ve fyzice, má symetrické rozložení kolem střední hodnoty. Pro každou kladnou odchylku od střední hodnoty bychom při velkém souboru hodnot našli stejně velkou zápornou odchylku. Toto rozložení se nazývá normální neboli Gaussovo rozložení a je popsáno funkcí

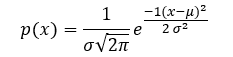
Gaussovo rozložení je známá křivka ve tvaru zvonu, která vyjadřuje hustotu pravděpodobností hodnot veličiny x (jsou to všechny hodnoty x_i, jež by při našem měření mohla nazývat tato fyzikální veličina). Hodnoty x_i jsou diskrétní, ale pro n → ∞ jsou rozloženy tak hustě, že je můžeme aproximovat spojitým rozložením.

Rozptýlenost hodnot na číselné ose vyjadřuje veličina 𝜎², jež se nazývá rozptyl. Je definována jako průměrný čtverec odchylek jednotlivých hodnot od střední hodnoty µ.

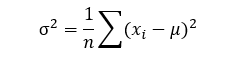
Druhá odmocnina rozptylu se nazývá směrodatná (standardní) odchylka 𝜎, někdy také střední kvadratická odchylka.

Platné číslice

Je nutné zmínit i časté chyby vzniklé při zapisování výsledků. Platné číslice jsou čísla odečtená ze stupnice, včetně posledního odhadnutého místa. Tento pojem se ale v různých případech liší. Obsahuje-li číslo mezi desetinnou čárkou a první nenulovou číslicí nuly, tak se nuly nepovažují za platné číslice. Naopak nuly za nenulovými číslicemi ve výsledku vyjádřeném desetinným číslem jsou platnými číslicemi. Nuly na konci výsledku neobsahujícího desetinnou čárku, mohou nebo nemusí být platnými číslicemi. Záleží totiž na nepřesnosti měření, z toho důvodu se pro jednoznačnost používá exponenciální zápis: jedno místo před desetinnou čárkou, desetinná místa odpovídající přesnosti měření, exponent a jednotka.

Příklad:

• 0,000406 → 3 platné číslice
• 0,0100 → 3 platné číslice

Měření objemu

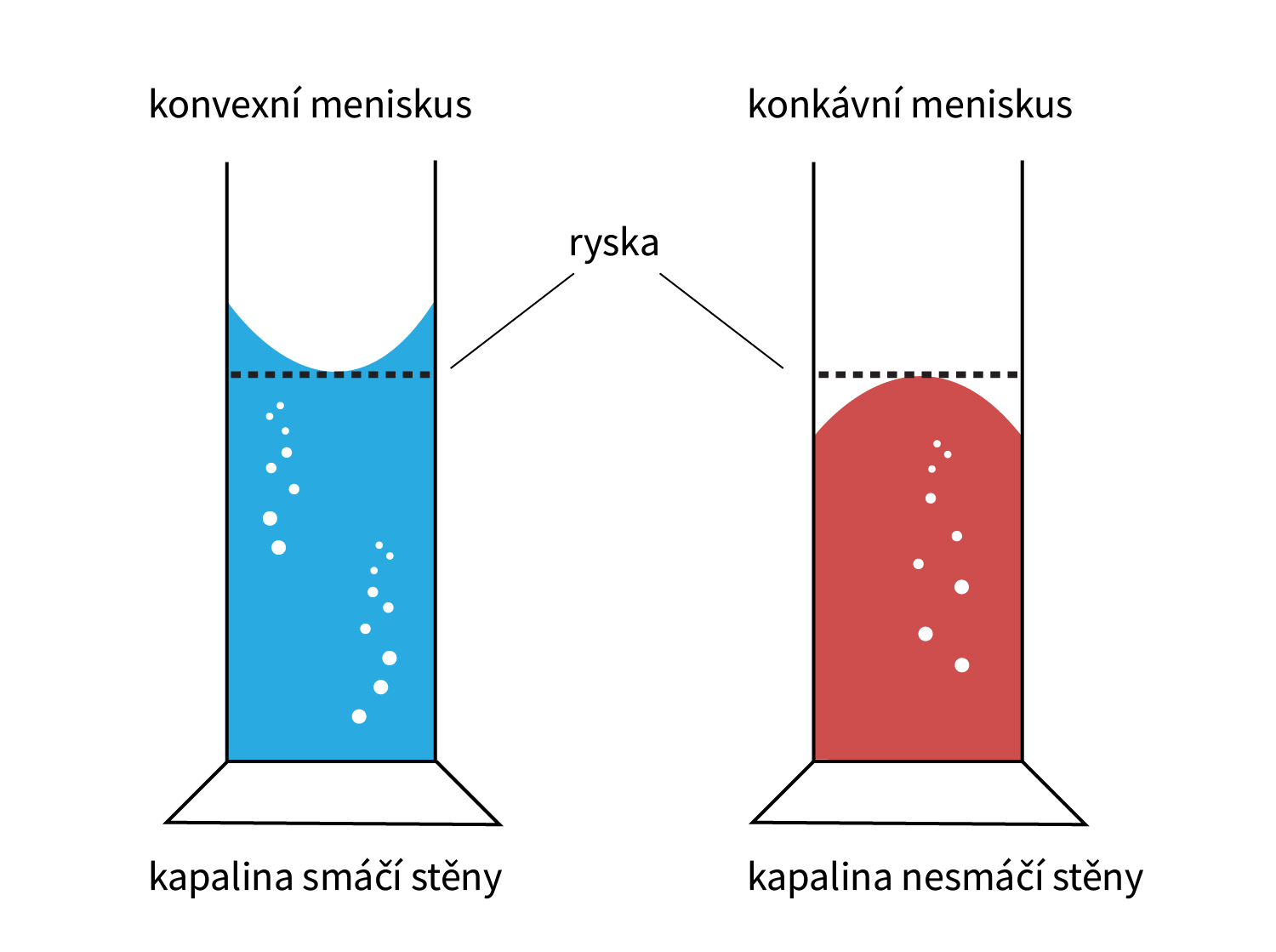
Objemy kapalin měříme pomocí odměrných nádob, mezi něž patří odměrné válce, pipety, byrety a odměrné baňky. Obecně platí, že objem (V) je fyzikální veličina závislá na teplotě. Proto je nutné, abychom objem měřili při konstantní teplotě.

Na každé odměrné nádobě je uvedena kalibrační teplota, která je většinou 20 °C. Rozlišuje se také kalibrace na dolití (značeno IN, D – dolití, E – einguss, případně C – contains) nebo na vylití (EX, V – vylití, A – ausguss či D – delivers). Při vylití z nádoby, která je určena na dolití získáme menší množství kapaliny, než je udáno, jelikož trochu kapaliny ulpívá na jejích stěnách. Avšak z nádob kalibrovaných na vylití (pipety, byrety) dostaneme při vylití přesný objem kapaliny, který je na nádobě udán. Při správném měření objemu, musíme dbát na správné odečítání povrchu kapalin, protože kapalina v závislosti na svém povrchovém napětí smáčí stěny nádoby a tvoří tzv. meniskus. Spodní část menisku (konvexní meniskus) u látek nebarevných a látek, které smáčejí stěny nádoby, musí být na rysce. Naopak u látek barevných a látek, které nesmáčejí stěny nádoby, musí horní meniskus (konkávní meniskus) ležet na rysce.