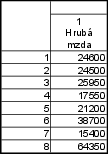
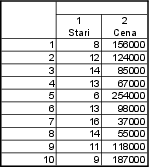
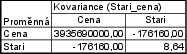
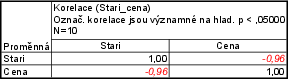
Vypočítejte medián hrubé měsíční mzdy a kvartilové rozpětí. Byly zjištěny tyto hodnoty v Kč: 24 600, 24 500, 25 950, 17 550, 21 200, 38 700, 15 400, 64 350.
Zjistěte:
- medián
- nejdříve hodnoty seřadíme podle velikosti:
15 400, 17 550, 21 200, 24 500, 24 600, 25 950, 38 700, 64 350 - pozorování je celkem 8 $ \Rightarrow n=8$
- chceme vypočítat medián $ \Rightarrow \alpha=0,5$
- hodnota $n\alpha=8\cdot 0,5=4 \Rightarrow $ vyšlo nám celé číslo $ \Rightarrow c=4$
- pro výpočet budeme tedy potřebovat 4. a 5. číslo v seřazené řadě
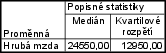
- $ x_{0,50}=\frac{x_{(4)}+x_{(5)}}{2} = \frac{24\,500+2\,600}{2} = 24\,550$
- nejdříve hodnoty seřadíme podle velikosti:
- kvartilové rozpětí
- nejdříve spočítáme $ x_{0,25}$ a $ x_{0,75} $
- výpočet provedeme stejně jako v předchozím případě, pouze za $ \alpha $ budeme volit jiná čísla
- pozorování je celkem 8 $ \Rightarrow n=8$
- chceme vypočítat dolní kvartil $ \Rightarrow \alpha=0,25$
- hodnota $n\alpha=8\cdot 0,25=2 \Rightarrow $ vyšlo nám celé číslo $ \Rightarrow c=2$
- pro výpočet budeme tedy potřebovat 2. a 3. číslo v seřazené řadě
- $ x_{0,25}=\frac{x_{(2)}+x_{(3)}}{2} = \frac{17\,550+21\,200}{2} = 19\,375$
- chceme vypočítat horní kvartil $ \Rightarrow \alpha=0,75$
- hodnota $n\alpha=8\cdot 0,75=6 \Rightarrow $ vyšlo nám celé číslo $ \Rightarrow c=6$
- pro výpočet budeme tedy potřebovat 6. a 7. číslo v seřazené řadě
- $ x_{0,75}=\frac{x_{(6)}+x_{(7)}}{2} = \frac{25\,950+38\,700}{2} = 32\,325$
- kvartilové rozpětí je $ x_{0,75} - x_{0,25} = 32\,325 - 19\,375 = 12\,950$