Statistika | Přírodovědecká fakulta Masarykovy univerzity

Regresní analýza

V regresní analýze pracujeme se závislou proměnnou $Y$ (s hodnotami znaku $ Y $) a s nezávislými proměnnými $X_1,X_2,\dots, X_k$ (s hodnotami znaků $X_1,X_2,\dots, X_k$).

Cílem regresní analýzy je zkoumání závislosti mezi $Y$ a $X_1,X_2,\dots, X_k$, jinak řečeno zkoumá vliv hodnot znaků $X_1,X_2,\dots, X_k$ na hodnoty znaku $Y$.

K určení této závislosti je potřeba najít vhodnou funkci, která bude nejlépe aproximovat $Y$ (funkce může být lineární, kvadratická, polynomiální, …).

My se omezíme pouze na případ, kdy hledaná vhodná funkce bude lineární a budeme mít pouze jednu nezávislou proměnnou.

\[y=\beta_0 + \beta_1 x\]

Jedná se tedy o přímku.

Dále budeme odhadovat koeficienty $ \beta_0,\beta_1$, jejich odhady budeme značit $ b_0, b_1$.

Abychom mohli odhadnout regresní koeficienty musíme pořídit $ n $ dvojic pozorování $(x_i, y_i)$, kde $i=1, \dots, n.$

$ x_i $ je skutečná $ i $-tá hodnota znaku $ X $
$ y_i $ je skutečná $ i $-tá hodnota znaku $ Y $

Regresní funkci (přímku) pak dostaneme, když za koeficienty dosadíme jejich odhady \[ y=b_0 + b_1x \]

$b_0$ udává velikost posunutí přímky na ose y
$b_1$ je směrnicí přímky a udává, o kolik jednotek se změní hodnota znaku $ Y $, změní-li se hodnota znaku $ X $ o jednotku. Pokud je $b_1$ kladné, mluvíme o přímé závislosti hodnot znaku $ Y $ na hodnotách znaku $ X $, pokud je $b_1$ záporné, mluvíme o nepřímé závislosti hodnot znaku $ Y $ na hodnotách znaku $ X $

Regresní odhad $ i $-té hodnoty znaku $Y$ \[ \hat{y_i}=b_0 + b_1x_i \]

Nejpoužívanější metoda při získávání odhadu koeficientů je metoda nejmenších čtverců. Je založená na minimalizování součtu čtverců odchylek.

součet odchylek je: \[\sum_{i=1}^n \bigl(y_i-\beta_0 - \beta_1 x_i \bigr)\]
součet čtverců odchylek je pak tvaru: \[\sum_{i=1}^n \bigl(y_i-\beta_0 - \beta_1 x_i \bigr)^2\]
minimalizování součtu čtverců odchylek provedeme postupnými parciálními derivacemi podle koeficientů
- parciální derivace podle $\beta_0$: \[2 \cdot \sum_{i=1}^n \bigl(y_i-\beta_0 - \beta_1 x_i \bigr) \cdot(-1)\]
- parciální derivace podle $\beta_1$: \[2 \cdot \sum_{i=1}^n \bigl(y_i-\beta_0 - \beta_1 x_i \bigr) \cdot(-x_i)\]
parciální derivace pak vždy položíme rovny nule a řešíme soustavu 2 rovnic o 2 neznámých $ \beta_0, \beta_1 $
řešením systému rovnic jsou odhady $ b_0, b_1 $: $$ b_0=m_2-\frac{s_{12}}{s_1^{2}}m_1 $$ $$ b_1=\frac{s_{12}}{s_1^{2}} $$ po dosazení do regresní přímky dostáváme $ y=m_2+\frac{s_{12}}{s_1^{2}}(x-m_1)$

Grafické znázornění:

mějme tabulku se skutečnými hodnotami:

$ x_i $

$ y_i $

0,50

4,32

5,00

8,90

9,14

do grafu vyznačíme body $[x_i,y_i]$

body proložíme regresní přímkou $y=b_0+b_1x$

následující graf zachycuje odchylky

na grafu jsou zachyceny čtverce odchylek

Reziduální součet čtverců znaku $Y$ kolem regresní funkce \[ s_E^2=\sum_{i=1}^n (y_i-\hat{y_i})^2 \]

Celkový součet čtverců znaku $Y$ \[ s_T^2=\sum_{i=1}^n (y_i-m_2 )^2 \]

Regresní součet čtverců regresních odhadů znaku $Y$ kolem průměru $m_2$ \[ s_R^2=\sum_{i=1}^n (\hat{y_i}-m_2 )^2 \]

Index determinace \[ ID^2=\frac{s_R^2}{s_T^2} \]

platí, že $s_T^2=s_E^2+s_R^2 \Rightarrow s_R^2=s_T^2-s_E^2$, pokud dosadíme do indexu determinace, dostaneme: \[ ID^2=\frac{s_T^2-s_E^2}{s_T^2}=1-\frac{s_E^2}{s_T^2} \]
z $s_T^2=s_E^2+s_R^2$ víme, že $ s_E^2\leq s_T^2 \Rightarrow 0\leq ID^2\leq 1 $
interpretace indexu determinace:
například pokud $ID^{2}=0,65$, znamená to, že regresní přímka vysvětluje 65% variability hodnot znaku $ Y $.

Příklad 5.1:

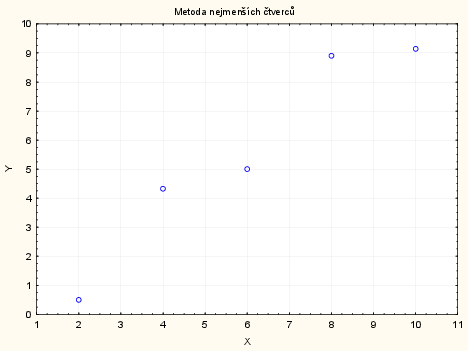
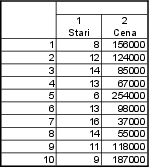
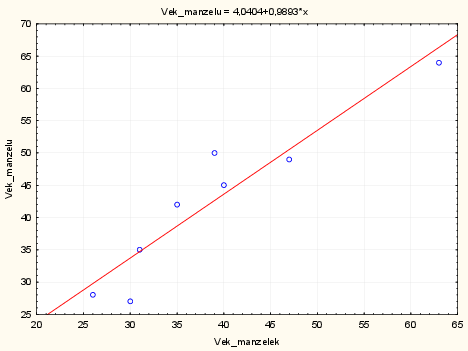
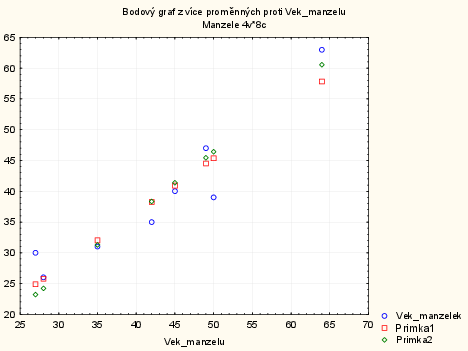
Vrátíme se k příkladu se stářím a cenami aut. Tentokrát nás bude zajímat závislost ceny aut na stáří aut. V následující tabulce jsou zaznamenány ceny aut v tisících a jejich stáří v letech, jedná se o vozy stejné značky. Zjistěte regresní přímku a index determinace.

stáří auta	8	12	14	13	6	13	16	14	11	9
cena auta	156	124	85	67	254	98	37	55	118	187

postup

postup v programu Statistica

proměnná $ X $ bude stáří aut a proměnná $ Y $ bude cena aut
budeme hledat regresní přímku a odhady $ b_0, b_1 $ takové, aby součet čtverců odchylek byl co nejmenší $ \Rightarrow $ použijeme tedy metodu nejmenších čtverců
výpočet $ b_0 $
- $ b_0$ vypočítáme pomocí vzorce $$ b_0=m_2-\frac{s_{12}}{s_1^{2}}m_1 $$
- z předchozích výpočtů víme, že $m_1=11,6, m_2=118\,100 , s_{12}= -176\,160 $ a $ s_1^{2}=8,64 $
- dosazením do vzorce tedy dostáváme $$ b_0=118\,100-\frac{-176\,160}{8,64}\cdot 11,6=354\,611,1 $$
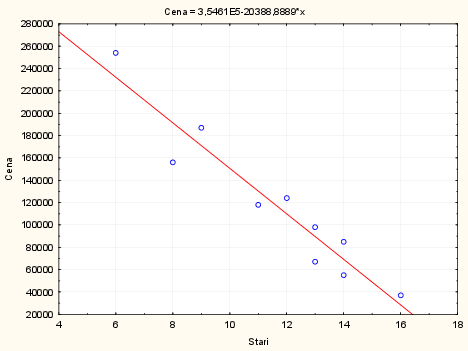
- to znamená, že přímka je posunutá na svislé ose o 354 611,1.
výpočet $ b_1 $
- $ b_1 $ vypočítáme pomocí vzorce $$ b_1=\frac{s_{12}}{s_1^{2}} $$
- z předchozích výpočtů víme, že $ s_{12}= -176\,160 $ a $ s_1^{2}=8,64 $
- dosazením do vzorce tedy dostáváme $$ b_1=\frac{-176\,160}{8,64}=-20\,388,89 $$
- to znamená, že směrnice přímky je -20388,89, protože $ b_1 \lt 0 $ hodnoty znaku $Y$ jsou na hodnotách znaku $X$ nepřímo závislé
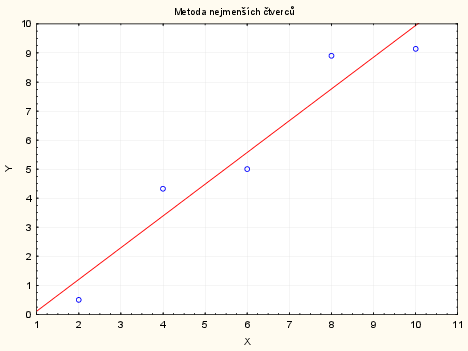
regresní přímka je tedy tvaru $$ y=354\,611,1-20\,388,89x $$
reziduální součet čtverců
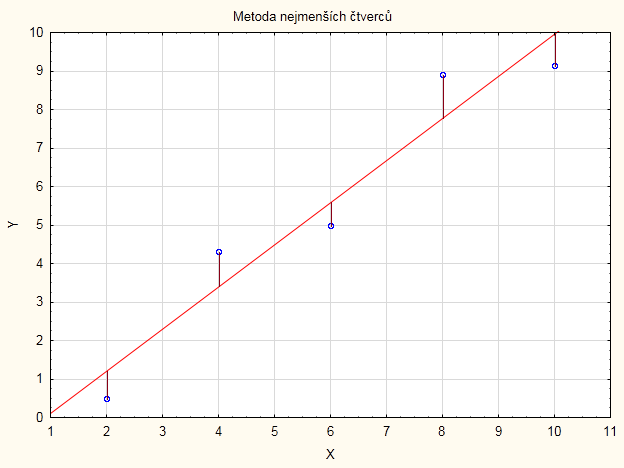
- reziduální součet čtverců spočítáme ze vzorce: \[ s_E^2=\sum_{i=1}^{10} (y_i-\hat{y_i})^2 \]
- nejdříve spočítáme regresní odhady $\hat{y_i}$, které dostaneme dosazováním $x_i$ do regresní přímky:
  - $\hat{y_1}=354611,1-20388,89\cdot8=191\,500$
  - $\hat{y_2}=354611,1-20388,89\cdot12=109\,944,4$
  - $\hat{y_3}=354611,1-20388,89\cdot14=69\,166,64$
  - $\hat{y_4}=354611,1-20388,89\cdot13=89\,555,53$
  - $\hat{y_5}=354611,1-20388,89\cdot6=232\,277,8$
  - $\hat{y_6}=354611,1-20388,89\cdot13=89\,555,53$
  - $\hat{y_7}=354611,1-20388,89\cdot16=28\,388,86$
  - $\hat{y_8}=354611,1-20388,89\cdot14=69\,166,64$
  - $\hat{y_9}=354611,1-20388,89\cdot11=130\,333,3$
  - $\hat{y_{10}}=354611,1-20388,89\cdot9=171\,111,1$
- po dosazení do vzorce dostáváme: $$\begin{align*} s_E^2&=(156\,000-191\,500)^2+(124\,000-109\,944,4)^2+\\&+(85\,000-69\,166,64)^2+(67\,000-89\,555,53)^2+\\&+(254\,000-232\,277,8)^2+(98\,000-89\,555,53)^2+\\&+(37\,000-28\,388,86)^2+(55\,000-69\,166,64)^2+\\&+(118\,000-130\,333,3)^2+(187\,000-171\,111,1)^2=\\&=3\,439\,833\,013 \end{align*}$$
celkový součet čtverců
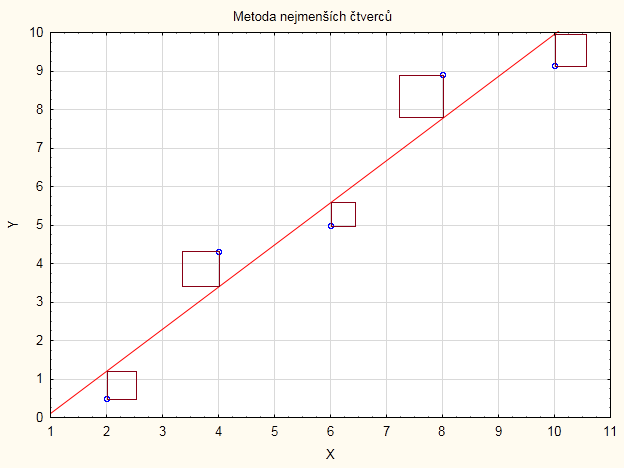
- celkový součet čtverců spočítáme ze vzorce: \[ s_T^2=\sum_{i=1}^{10} (y_i-m_2 )^2 \]
- víme, že $ m_2=118\,100 $ a $y_i$ máme v tabulce v zadání
- po dosazení do vzorce dostáváme: $$\begin{align*} s_T^2&=(156\,000-118\,100)^2+(124\,000-118\,100)^2+\\&+(85\,000-118\,100)^2+(67\,000-118\,100)^2+\\&+(254\,000-118\,100)^2+(98\,000-118\,100)^2+\\&+(37\,000-118\,100)^2+(55\,000-118\,100)^2+\\&+(118\,000-118\,100)^2+(187\,000-118\,100)^2=\\&=39\,356\,900\,000 \end{align*}$$
index determinace spočítáme pomocí vzorce \[ID^2=1-\frac{s_E^2}{s_T^2}\]
po dosazení do vzorce dostáváme: \[ID^2=1-\frac{3\,439\,833\,013}{39\,356\,900\,000}=0,9126\]
index determinace nám říká, že proměnná stáří aut vysvětluje 91,26 % variability ceny aut

Příklad 5.2:

U osmi manželských párů byl zjišťován věk manželů a manželek. Zjištěné hodnoty zachycuje následující tabulka:

Věk manželů	45	50	35	64	42	27	49	28
Věk manželek	40	39	31	63	35	30	47	26

Určete regresní přímku věku manželek na věk manželů a index determinace
Určete regresní přímku věku manželů na věk manželek a index determinace
Graficky znázorněte obě regresní přímky do jednoho grafu

Věk manželů označíme $X$ a věk manželek označíme $Y$. Dále musíme zjistit průměrný věk manželů $m_1$, průměrný věk manželek $m_2$, směrodatnou odchylku a rozptyl věku manželů $s_1$, $s_1^2$, směrodatnou odchylku a rozptyl věku manželek $s_2, s_2^2$ a kovarianci $s_{12}$.

$m_1=\frac{1}{8}\cdot (45+50+35+64+42+27+49+28)=42,5$
$m_2=\frac{1}{8}\cdot (40+39+31+63+35+30+47+26)=38,88$
$\begin{align}s_1^2&=\frac{1}{8}\cdot \bigl((45-42,5)^2+(50-42,5)^2+(35-42,5)^2+(64-42,5)^2+\\&+(42-42,5)^2+(27-42,5)^2+(49-42,5)^2+(28-42,5)^2 \bigr)=\\&=134,25\end{align}$
$s_1=\sqrt{134,25}=11,59$
$\begin{align}s_2^2&=\frac{1}{8}\cdot \bigl( (40-38,88)^2+(39-38,88)^2+(31-38,88)^2+\\&+(63-38,88)^2+(35-38,88)^2+(30-38,88)^2+\\&+(47-38,88)^2+(26-38,88)^2\bigr)=121,36\end{align}$
$s_2=\sqrt{121,36}=11,02$
$\begin{align}s_{12}&=\frac{1}{8}\cdot (45\cdot 40+50\cdot39+ 35\cdot31+64\cdot63+42\cdot35+27\cdot30+\\&+49\cdot47+28\cdot26 )-42,5\cdot38,88=120,06\end{align}$

postup

postup v programu Statistica

regresní přímka věku manželek na věk manželů
- $y=b_0+b_1x$
- $ y=m_2+\frac{s_{12}}{s_1^2}(x-m_2)$
- dosazením do vzorce dostaneme: \[ y=38,88+\frac{120,06}{134,25}(x-42,5)\]
- výsledná regresní přímka je: \[ y=0,87 + 0,89x \]
regresní přímka věku manželů na věk manželek
- $ x=\overline{b}_0+\overline{b}_1y$
- $ x=m_1+\frac{s_{12}}{s_2^2}(y-m_2)$
- dosazením do vzorce dostaneme: \[ x=42,5+\frac{120,06}{121,36}(y-38,88) \]
- výsledná regresní přímka je: \[x=4,04+0,99y \]
- Regresní přímka věku manželek na věk manželů je $y=0,87+0,89x$, označíme ji přímka1.
- Regresní přímka věku manželů na věk manželek je $x=4,04+0,99y$, nejdříve z ní vyjádříme $y$ pomocí $x$ $\Rightarrow y=(-4,04+x)/0,99$ a označíme ji přímka2.

Nejdříve vytvoříme nový datový soubor o 2 proměnných a 8 případech a tabulku vyplníme podle zadání.

Interaktivní tutoriál

Videotutoriál

Statistiky – Vícenásobná lineární regrese – Proměnné – Závislá prom.: Vek_manzelek, Nezávislá prom.: Vek_manzelu – OK – Výpočet: Výsledky regrese.

Grafy–2D grafy – Bodové grafy – Proměnné: X:Vek_manzelu, Y:Vek_manzelek – OK.

Regresní přímka je ve tvaru $y=0,87+0,89x$. Index determinace je 0,8848 $ \Rightarrow $ regresní funkce vysvětluje 88,48 % variability věku manželek.

Interaktivní tutoriál

Videotutoriál

Statistiky – Vícenásobná lineární regrese – Proměnné – Závislá prom.: Vek_manzelu, Nezávislá prom.: Vek_manzelek – OK – Výpočet: Výsledky regrese.

Grafy–2D grafy – Bodové grafy – Proměnné: X:Vek_manzelek, Y:Vek_manzelu – OK.

Regresní přímka je ve tvaru $x=4,04+0,99y$. Index determinace je 0,8848 $ \Rightarrow $ regresní funkce vysvětluje 88,48 % variability věku manželů.

Interaktivní tutoriál

Videotutoriál

Nejdříve vytvoříme nový datový soubor o 4 proměnných a 8 případech. Tabulku vyplníme, aby vypadala takto:

Dvakrát klikneme na proměnnou Primka1 a do dlouhého jména napíšeme =0,87+0,89*v1 – OK – Ano.

Dvakrát klikneme na proměnnou Primka2 a do dlouhého jména napíšeme =(-4,04+v1)/0,99 – OK – Ano.

Dostaneme následující tabulku:

Dále pokračujeme: Grafy – 2D grafy – Bodové grafy – Proměnné – X: Vek_manzelu, Y: Vek_manzelek, Primka1, Primka2 – OK – Typ grafu: Vícenásobný – Typ proložení: odškrtneme – OK.

Dostaneme následující graf:

Dvakrát klikneme na libovolný červený čtverec – odškrtneme značky a zaškrtneme spojnice – OK.

Dvakrát klikneme na libovolný zelený kosočtverec – odškrtneme značky a zaškrtneme spojnice – OK.

Dvakrát klikneme na graf – Graf – Nadpisy/text – Graf regresních přímek – Osa – Název – Osa: Y vlevo – Vek_manzelek – OK.

Ještě odstraníme podnadpis a první popisek v legendě a výsledný graf vypadá takto:

Vidíme, že přímky svírají malý úhel, to znamená, že mezi věkem manželů a manželek existuje silná přímá lineární závislost.