Vážené číselné charakteristiky znaků

1. Vážený průměr
   • k výpočtu váženého průměru použijeme vzorec $$m=\frac{1}{n}\sum_{j=1}^r n_jx_{[j]}$$
   • vážený průměr 8.A označíme $ m_A $ a 8.B označíme $ m_B $
   • nejdříve spočítáme vážený průměr 8.A:
     • žáků je 28 $\Rightarrow n=28$
     • body budou hodnoty znaku $x_{[1]}=1, \dots , x_{[5]}=5$
     • počty žáků budou absolutní četnosti
     • po dosazení do vzorce: $$\begin{align} m_A&=\frac{1}{28}\sum_{j=1}^5 n_{1j}x_{[j]}=\\&=\frac{1}{28}\cdot(7\cdot 1+8\cdot 2+7\cdot 3+4\cdot 4+2\cdot 5)= 2,5 \end{align}$$
     • vážený průměr v 8.A je tedy 2,5
   • stejným způsobem spočítáme i vážený průměr v 8.B
     • žáků je 31 $\Rightarrow n=31$
     • body budou hodnoty znaku $x_{[1]}=1, \dots , x_{[5]}=5$
     • počty žáků budou absolutní četnosti
     • po dosazení do vzorce: $$\begin{align} m_B&=\frac{1}{31}\sum_{k=1}^5 n_{2j}x_{[j]}=\\&=\frac{1}{31}\cdot(8\cdot 1+10\cdot 2+6\cdot 3+4\cdot 4+3\cdot 5)= 2,48 \end{align}$$
     • vážený průměr v 8.B je tedy 2,48
2. Vážený rozptyl
   • k výpočtu váženého rozptylu použijeme vzorec $$s^2=\frac{1}{n}\sum_{j=1}^r n_j(x_{[j]}-m)^2$$
   • vážený rozptyl 8.A označíme $ s^2_A $ a 8.B označíme $ s^2_B $
   • nejdříve spočítáme vážený rozptyl 8.A:
     • žáků je 28 $\Rightarrow n=28$
     • body budou hodnoty znaku $x_{[1]}=1, \dots , x_{[5]}=5$
     • počty žáků budou absolutní četnosti
     • vážený průměr jsme spočítali v předchozím případě $\Rightarrow m_A=2,5 $
     • dosadíme do vzorce: $$s_A^2=\frac{1}{28}\sum_{j=1}^5 n_{1j}(x_{[j]}-m_A)^2$$
     • po dosazení: $$\begin{align} &\frac{1}{28}\cdot \bigl( 7\cdot(1-2,5)^2+8\cdot(2-2,5)^2+\\&+7\cdot(3-2,5)^2+4\cdot(4-2,5)^2+2\cdot(5-2,5)^2\bigr) \end{align}$$
     • vážený rozptyl v 8.A je $ s_A^2=1,46 $
   • stejným způsobem spočítáme i vážený rozptyl v 8.B
     • žáků je 31 $\Rightarrow n=31$
     • body budou hodnoty znaku $x_{[1]}=1, \dots , x_{[5]}=5$
     • počty žáků budou absolutní četnosti
     • vážený průměr jsme spočítali v předchozím případě $\Rightarrow m_B=2,48 $
     • dosadíme do vzorce: $$s_B^2=\frac{1}{31}\sum_{j=1}^5 n_{2j}(x_{[j]}-m_B)^2$$
     • po dosazení: $$\begin{align} &\frac{1}{31}\cdot \bigl( 8\cdot(1-2,48)^2+10\cdot(2-2,48)^2+6\cdot(3-2,48)^2+\\&+4\cdot(4-2,48)^2+3\cdot(5-2,48)^2\bigr) \end{align}$$
     • vážený rozptyl v 8.B je $ s_B^2=1,60 $
   • zjistili jsme, že větší průměr i menší rozptyl byl v 8.A.

8.A

8.B

Nejdříve vytvoříme nový datový soubor o 3 proměnných (Body, 8.A, 8.B) a 5 případech, tabulku vyplníme podle zadání:

Statistiky – Základní statistiky a tabulky – Popisné statistiky – Proměnná: Body – OK – nastavíme váhy – Proměnná vah: 8.A – vybereme zapn.– Detailní výsledky – zrušíme označení u Počet platn., Minimum $\&$ maximum a zaškrtneme Rozptyl – Výpočet.

Pro zaokrouhlení na dvě desetinná místa se kurzorem nastavíme na danou proměnnou v nové tabulce a dvakrát klikneme – Desetinná místa: 2 – OK.

Dvakrát klikneme na proměnnou Rozptyl – Dlouhé jméno: =v2*27/28 – OK.

U 8.B bude postup v programu Statistica stejný, pouze Proměnná vah bude 8.B a do Dlouhého jména napíšeme: =v2*30/31.

• pro výpočet použijeme vzorec $$m_1=\frac{1}{n}\sum_{j=1}^r n_{j\cdot}x_{[j]}$$
• počet soutěžících je 37 $ \Rightarrow n=37$
• za $x_{[j]}$ budeme dosazovat střed $ j $-tého třídicího intervalu znaku $X$
• za $n_{j\cdot}$ budeme dosazovat marginální absolutní četnost $ j $-tého třídicího intervalu znaku $X$
• po dosazení do vzorce $$m_1=\frac{1}{37}\sum_{j=1}^2 n_{j\cdot}x_{[j]}=\frac{1}{37}\cdot\bigl(17\cdot 22,5+20\cdot 37,5 \bigr)$$
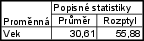
• konečný výsledek je $ m_1=30,61 $

• pro výpočet použijeme vzorec $$s_1^2=\frac{1}{n}\sum_{j=1}^r n_{j\cdot}(x_{[j]}-m_1)^2$$
• počet soutěžících je 37 $ \Rightarrow n=37$
• za $x_{[j]}$ budeme dosazovat střed $ j $-tého třídicího intervalu znaku $X$
• za $n_{j\cdot}$ budeme dosazovat marginální absolutní četnost $ j $-tého třídicího intervalu znaku $X$
• z předchozího výpočtu víme, že $ m_1=30,61 $
• po dosazení do vzorce $$\begin{align} s_1^2&=\frac{1}{37}\sum_{j=1}^2 n_{j\cdot}(x_{[j]}-30,61)^2=\\&=\frac{1}{37}\cdot\bigl(17\cdot (22,5-30,61)^2+20\cdot (37,5-30,61)^2 \bigr) \end{align}$$
• konečný výsledek je $ s_1^2= 55,88$

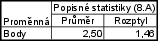
Vytvoříme nový datový soubor o 2 proměnných a 2 případech. Tabulku vyplníme následovně:

Základní statistiky a tabulky – Popisné statistiky – Proměnná: Vek – OK – nastavíme váhy – Proměnná vah: Cetnost – vybereme zapn.– Detailní výsledky – zrušíme označení u Počet platn., Minimum $\&$ maximum, Směrodatná odchylka a zaškrtneme Rozptyl – Výpočet.

Pro zaokrouhlení na dvě desetinná místa se kurzorem nastavíme na danou proměnnou v nové tabulce a dvakrát klikneme – Desetinná místa: 2 – OK.

Dvakrát klikneme na proměnnou Rozptyl – Dlouhé jméno: =v2*36/37 – OK.

• pro výpočet použijeme vzorec $$m_2=\frac{1}{n}\sum_{k=1}^s n_{\cdot k}y_{[k]}$$
• počet soutěžících je 37 $ \Rightarrow n=37$
• za $y_{[k]}$ budeme dosazovat střed $ k $-tého třídicího intervalu znaku $Y$
• za $n_{\cdot k}$ budeme dosazovat marginální absolutní četnost $ k $-tého třídicího intervalu znaku $Y$
• po dosazení do vzorce $$m_2=\frac{1}{37}\sum_{k=1}^3 n_{\cdot k}y_{[k]}=\frac{1}{37}\cdot\bigl(10\cdot 10+13\cdot 30+14\cdot 50 \bigr)$$
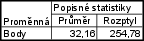
• konečný výsledek je $ m_2=32,16 $

• pro výpočet použijeme vzorec $$s_2^2=\frac{1}{n}\sum_{k=1}^s n_{\cdot k}(y_{[k]}-m_2)^2$$
• počet soutěžících je 37 $ \Rightarrow n=37$
• za $y_{[k]}$ budeme dosazovat střed $ k $-tého třídicího intervalu znaku $Y$
• za $n_{\cdot k}$ budeme dosazovat marginální absolutní četnost $ k $-tého třídicího intervalu znaku $Y$
• z předchozího výpočtu víme, že $ m_2=32,16 $
• po dosazení do vzorce $$\begin{align} s_2^2&=\frac{1}{37}\sum_{k=1}^3 n_{\cdot k}(y_{[k]}-32,16)^2=\\&=\frac{1}{37}\cdot\bigl(10\cdot (10-32,16)^2+13\cdot (30-32,16)^2+\\&+14\cdot (50-32,16)^2 \bigr) \end{align}$$
• konečný výsledek je $ s_2^2=254,78 $

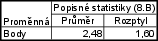
Vytvoříme nový datový soubor o 2 proměnných a 3 případech. Tabulku vyplníme následovně:

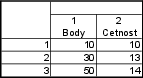
Základní statistiky a tabulky – Popisné statistiky – Proměnná: Body – OK – nastavíme váhy – Proměnná vah: Cetnost – vybereme zapn.– Detailní výsledky – zrušíme označení u Počet platn., Minimum $\&$ maximum, Směrodatná odchylka a zaškrtneme Rozptyl – Výpočet.

Pro zaokrouhlení na dvě desetinná místa se kurzorem nastavíme na danou proměnnou v nové tabulce a dvakrát klikneme – Desetinná místa: 2 – OK.

Dvakrát klikneme na proměnnou Rozptyl – Dlouhé jméno: =v2*36/37 – OK.

• pro výpočet použijeme vzorec $$s_{12}=\frac{1}{n}\sum_{j=1}^r \sum_{k=1}^s n_{jk}(x_{[j]}-m_1)(y_{[k]}-m_2)$$
• počet soutěžících je 37 $ \Rightarrow n=37$
• za $x_{[j]}$ budeme dosazovat střed $ j $-tého třídicího intervalu znaku $X$, za $y_{[k]}$ budeme dosazovat střed $ k $-tého třídicího intervalu znaku $Y$
• za $n_{jk} $ budeme dosazovat absolutní četnost $(j,k)$–tého třídicího intervalu
• z předchozího výpočtu víme, že $ m_1=30,61 $, $ m_2=32,16 $
• po dosazení do vzorce $$\begin{align} s_{12}&=\frac{1}{37}\sum_{j=1}^2 \sum_{k=1}^3 n_{jk}(x_{[j]}-30,61)(y_{[k]}-32,16)=\\&=\frac{1}{37}\bigl(7(22,5-30,61)(10-32,16)+\\&+4(22,5-30,61)(30-32,16)+\\&+6(22,5-30,61)(50-32,16)+\\&+3(37,5-30,61)(10-32,16)+\\&+9(37,5-30,61)(30-32,16)+\\&+8(37,5-30,61)(50-32,16) \bigr) \end{align}$$
• konečný výsledek je $ s_{12}= 23,01 $

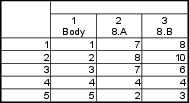
Nejdříve vytvoříme nový datový soubor o 3 proměnných a 6 případech. Tabulku vyplníme, aby vypadala takto:

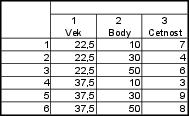
Statistiky -- Vícenásobná regrese -- Proměnné: Vek a Body (v tomto případě je jedno, která bude závislá, která nezávislá) -- OK -- nastavíme váhy -- Proměnná vah: Cetnost -- vybereme zapn. -- OK -- OK -- Residua/předpoklady/předpovědi -- Popisné statistiky -- Další statistiky -- Kovariance.

Dvakrát klikneme na proměnnou Vek -- Formát zobrazení: Číslo -- Desetinná místa: 2 -- Dlouhé jméno: =v1*36/37 -- OK.

Dvakrát klikneme na proměnnou Body -- Desetinná místa: 2 -- Dlouhé jméno: =v2*36/37 -- OK.

Výsledná tabulka vypadá takto:

• pro výpočet použijeme vzorec $$r_{12}=\frac{s_{12}}{s_1\cdot s_2}$$
• víme, že $ s_{12}= 23,01$
• dopočítáme $ s_1= \sqrt{s_1^2}= \sqrt{55,88}=7,48 $
• dopočítáme $ s_2= \sqrt{s_2^2}= \sqrt{254,78}=15,96 $
• nakonec dosadíme do vzorce $$r_{12}=\frac{23,01}{7,48\cdot 15,96}=\frac{23,01}{119,38}$$
• konečný výsledek je $ r_{12}=0,19 \Rightarrow $ mezi proměnnou věk a body existuje slabá přímá linerání závislost.

Nejdříve vytvoříme nový datový soubor o 3 proměnných a 6 případech. Tabulku vyplníme, aby vypadala takto:

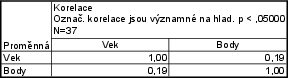
Statistiky -- Základní statistiky -- Korelační matice -- 1 seznam proměn. -- vybereme obě proměnné (Vek, Body) -- OK -- nastavíme váhy -- Proměnná vah: Cetnost -- vybereme zapn.-- OK -- Možnosti -- zrušíme zaškrtnutí u Včetně průměrů a sm. odch. ve čtverc. maticích -- Výpočet.

Opět dvakrát klikneme na proměnné Vek i Body a počet desetinných míst změníme na 2.

Dostaneme následující tabulku: