Mějme dáno n bodů roviny [xi,yi], kde i=1,...,n a předpokládejme, že leží na křivce blízké parabole s vrcholem v bodě [c,0] a protíná osu y, o rovnici:
![]()
Nechť jsou dále v této rovnici p,c reálná kladná čísla. Postupujme jako v případě aproximace elipsou, pak celkový součet čtverců relativních odchylek daných bodů od hledané paraboly je dán vztahem:
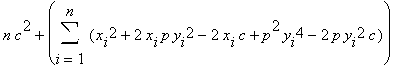
Jak jsme uvedli požadujeme, aby uvedený součet byl minimální. Hledejme tedy stacionární body dané funkce 2 proměnných (derivujeme součet nejdříve po řadě podle p a c), které tedy vyhovují zároveň rovnicím:


Tato lineární soustava 2 rovnic o 2 neznámých má jediné řešení pro n≥2 (právě hledané minimum):


Tak například je dáno n=5 bodů o souřadnicích:
![]()
![]()
![]()
![]()
![]()
Spočítejme jednotlivé dílčí sumy potřebné k výpočtu obou parametrů:
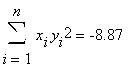



Jestliže se vyskytne ve jmenovatelech obou zlomků 0, pak daný postup nelze využít (soustava má nekonečně mnoho nebo žádné řešení) a je třeba přidat další (nebo odebrat některé) body, případně počítat v součtu se skutečnými Eukleidovskými vzdálenostmi bodů, či eliminovat odchylky metodou nejmenších čtverců.

Rozdíl vychází nenulový, tedy hodnoty parametrů hledané vhodné aproximace parabolou jsou:
![]()
![]()
Pro posouzení kvality našeho modelu můžeme sestrojit graf dané paraboly spolu se zadanými body:
