Tvar vajíčka částečně přípomíná kulovou plochu, avšak protaženou různě na obě protilehlé strany. Předpokládejme dále, že tento tvar odpovídá rotačnímu elipsoidu, který plynule přechází v rotační paraboloid (a jejichž osy jsou totožné). Umístíme-li skutečné vajíčko do kartézského souřadného systému, tak že jeho osa prochází osou x a křivka (kružnice), která spojuje body nejvíce vzdálené od této osy (průměr vajíčka), leží v rovně yz. Vajíčko dále orientujeme tak, aby jeho špička (tedy nejvzdálenější část od průměru vajíčka) ležela v poloprostoru daným hraniční rovinou yz a bodem kladné části osy x. Pak obrys řezu vajíčka rovinou xy bude blízký křivce, která je složena z části elipsy a na ní hladce napojené paraboly (viz. Hladké napojení elipsy a paraboly). Pokud máme takto umístěné vajíčko, pak můžeme přímo odečíst největší y-ovou souřadnici (parametr a) a nejmenší, resp. největší x-ovou souřadnici (parametr b, resp. c), odtud již lehce dopočítáme parametr p paraboly, aby došlo k hladkému napojení obou křivek (a zároveň průsečíky obou křivek). Přičemž rovnice těchto křivek dále považujme tvaru (elipsa a parabola):

![]()
Skutečný tvar vajíčka však není vždy zcela ideálně shodný s takto spočítanou křivkou. Do hry vstupuje mnoho náhodných faktorů, které se projeví jako odchylky skutečného tvaru od spočítané aproximace. Pokud bychom tvar vajíčka považovali pouze blízký jistému rotačnímu elipsoidu, minimalizace odchylek skutečného tvaru od aproximovaného by byla již snadná (viz. Aproximace pomocí elipsy). To odpovídá naší situaci v případě, že elipsa a parabola s dotýká právě ve společném vrchole.
Dále však předpokládejme, že tento předpoklad obecně neplatí. Z výše popsaného řezu můžeme určit polohy n bodů [xi,yi], i=1..n obrysu řezu vajíčkem (přibližně až na chyby měření). Je vhodné uvažovat větší počet bodů (n≥4) zvláště těch nejvíce vzdálených od osy y na obě strany. Dále tyto body seřadíme tak, aby platilo xi≤xj pro i<j, i,j=1..n. Pak zřejmě první 2 body budou vždy náležet elipse, zatímco poslední 2 body vždy parabole. Dále zřejmě existuje takový rozklad množiny těchto bodů do dvou tříd (v první třídě budou body s indexy 1..w a ve druhé body s indexy w+1..n, kde 2≤w≤n-2), podle nějž body první třídy leží na elipse a druhé třídy na parabole (za předpokladu, že tvar vajíčka je totožný z hledanou aproximací). Nevylučujeme však ani možnost, že bod [xw,yw] leží na parabole (pak je to zároveň bod dotyku elipsy s parabolou, ale obě třídy by pak nebyly disjunktní). Kdybychom znali hodnotu w, pak přímo určíme jednotlivé parametry elipsy i paraboly podle vztahů dříve odvozených:



My však tuto hodnotu neznáme. Nezbývá, než postupně projít všechny možnosti. Pro každou jednotlivě určit parametry a,b,c, zbylý parametr p je vhodnější dopočítat, aby došlo k hladkému napojení hledané elipsy a paraboly:

Pak určíme pro každý rozklad součet kvadrátů relativních odchylek a ty sečteme, čímž dostáváme vzorec (viz. Aproximace pomocí elipsy a Aproximace pomocí paraboly):

Určíme, který z těchto součtů je minimální a pak příslušné parametry považujme za nejvhodnější pro danou aproximaci (další možností je například jako parametry a,b,c vzít jejich průměr pro různé rozklady). Připomeňme, že až na případ, kdy jsou splněny předpoklady o shodnosti obou křivek, však existuje vhodnější aproximace (volba parametrů), kde Eukleidovské vzdálenosti naměřených bodů od teoreticky spočtených jsou v součtu menší. Statistickými metodami by bylo vhodné posoudit kvalitu dané aproximace včetně výpočtu pravděpodobnosti platnosti předpokladu o shodnosti křivek, což zde však provádět nebudeme.
Demonstrujme si vše na příkladu vajíčka poštolky obecné, přičemž máme dány přibližné souřadnice vybraných n=10 bodů ležících na obryse řezu vajíčka umístěného podle výše popsaných pravidel (měřítko v milimetrech):
![]()
w může nabývat hodnot 2 až 8. Ovšem je zřejmé, že body o záporných x-ových souřadnicích budou ležet na elipse, začněme tedy až hodnotou w=5 (menší lze bez újmy zanedbat).
pro w=5:
![]()
![]()
![]()
![]()
![]()
pro w=6:
![]()
![]()
![]()
![]()
![]()
pro w=7:
![]()
![]()
![]()
![]()
![]()
pro w=8:
![]()
![]()
![]()
![]()
![]()
Minimální součet vychází pro w=8, tedy příslušné rovnice do nekonečna prodloužených aproximačních křivek jsou:
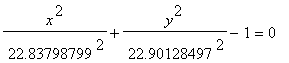
![]()
Na závěr ještě můžeme vizuálně posoudit vhodnost vybrané aproximace: